Определение оптимальных запасов

Говоря о размере текущего запаса, как правило, имеют в виду его максимальную, среднюю или минимальную величину. В случае если новая партия расходуемой продукции прибывает точно в момент окончания предыдущей, минимальная величина текущего запаса будет равна нулю, а средняя величина – половине максимальной. Очевидно, что при таком режиме поставок максимальный текущий запас будет равен размеру поставленной партии товара.

Оптимальным размером текущего запаса будем считать оптимальное значение его средней величины (Зтек.ср), равное половине заказанной и доставляемой партии товара. Таким образом, задача поиска оптимального размера запаса преобразуется в задачу поиска оптимального размера заказываемой партии товара.

Критерием оптимума является минимум общих затрат за период, связанных с созданием и содержанием запаса.

В системах управления запасами используются две категории затрат: затраты удельные и затраты за анализируемый период.

Затраты удельные представляют собой:

- затраты удельные на создание запасов, то есть затраты на размещение и получение одного заказа; измеряются в рублях и обозначаются символом К;

- затраты удельные на хранение запасов, то есть затраты на хранение единицы запаса в единицу времени; обозначаются символом М и имеют размерность руб./руб.×год или 1/год, если запас измеряется в денежных единицах.

В системах управления запасами в качестве единицы измерения времени при определении удельных затрат на хранение чаще всего принимают год. Таким образом, величина М показывает, какую часть от стоимости единицы продукции составляет стоимость ее хранения в течении года.

Затраты за период представляют собой:

- затраты на размещение и получение всех заказов, сделанных за период (Сзак);

- затраты на хранение среднего запаса в течение периода (Схран).

Общие затраты за период обозначаются символом Собщ. Затраты за период имеют размерность руб/период, например руб/год.

Помимо затрат удельных и затрат за период система управления запасами характеризуется также следующими параметрами:

Q – спрос на товар за период, шт/период;

Р – закупочная стоимость единицы товара, руб/шт;

Т – продолжительность анализируемого периода, год/период;

S – размер заказываемой партии товара, шт;

Зтек.ср – запас текущий средний, шт;

N – количество заказов за период (частота завоза), заказ/период;

t – промежуток между поставками, год/заказ.

Неуправляемыми параметрами в целевой функции очевидно являются удельные затраты на создание запаса (К) и удельные затраты на хранение запаса (М), а также спрос на товар за анализируемый период (Q), закупочная стоимость единицы товара (Р) и продолжительность анализируемого периода (Т). Остальные параметры, тесно связаны между собой, в рамках рассматриваемой задачи являются управляемыми, то есть менеджер может менять их по своему усмотрению, получая те или иные экономические результаты.

Следует иметь в виду, что задача оптимизация может быть решена в случае, если выполняются следующие условия:

- новая партия товара доставляется в момент полного расхода текущего запаса;

- потребность в материалах за период (спрос на товар) является величиной известной и постоянной (Q = const);

- удельные затраты на создание запасов известны и постоянны (К = const), то есть затраты на размещение и получение одного заказа не зависят от размера заказа;

- удельные расходы по хранению запаса известны и постоянны (М = const);

- закупочная стоимость товара постоянна и не зависит от размере закупаемой партии (Р = const).

Критерием оптимума является минимум суммы общих затрат за период. В связи с этим представим целевую функцию (Собщ) в виде суммы затрат за период на создание и хранение запасов и найдем такое значение размера заказа (Sопт), при котором общие затраты будут минимальны.

                   

                       Собщ = Схран + Сзак → min.                       (1.3)

 

Для решения задачи найдем зависимости Сзак и Схран от S.

Зависимость затрат за период на создание запасов от размера заказа.

Количество заказов за период (N) связано со спросом на товар за соответствующий период (Q) и размером заказа (S) следующим соотношением:

                

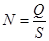                                 ,                                (1.4)

 

Затраты за период, связанные с размещением и получением заказов, рассчитывают по формуле (1.5).

 

                           Сзак = N × K                                         (1.5)

 

Изменение размера заказа (S) влечет за собой изменение количества заказов и соответствующее изменение затрат за период, связанных с размещением и получением заказов (Сзак).

Изменение размера заказа вызывает также изменение средней величины текущего запаса (Зтек.ср) и соответствующее изменение затрат за период на его хранение (Схран).

Расчет затрат за период на хранение запаса выполняют по формуле (1.6):

 

                       Схран = М × Т × Зтек.ср × Р                             (1.6)

 

Поскольку средняя величина текущего запаса равна половине заказа, то есть

                                 Зтек.ср = 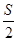,                                            (1.7)

 

то можно записать, что

 

Схран = М × Т × 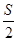 × Р.                           (1.8)

 

График зависимости Схран от S, имеющий, как правило, линейную форму, представлен на рисунке 1.1.

Из рисунка видно, что изменение размера заказа влечет за собой изменение затрат за период как на создание запаса, так и на его хранение. Однако характер зависимости каждой из этих статей расходов от размера заказа разный.

Затраты за период,

связанные с

хранением запасов,

Схран руб. за период

                                            Схран = М × Т × 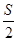 × Р

 

 

                                                                                  Размер заказа, S шт.

Рисунок 1.1 – Зависимость затрат за период, связанных с хранением запасов, от размера заказа

 

Суммарные затраты за период на создание запаса при увеличении размера заказа, очевидно, уменьшаются, так как закупки осуществляются более крупными партиями, и, следовательно, реже. Расходы по хранению за период растут прямо пропорционально размеру заказа.

Определим размер заказа (S), при котором минимизируются общие затраты:

 

Собщ = М × Т × 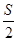 × Р + К ×  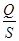→ min                                          (1.9)

 

В данном уравнении два управляемых параметра: S – независимая переменная Собщ – зависимая переменная. Остальные параметры являются постоянными коэффициентами. В упрощенной форме уравнение (1.9) примет вид:

 

Cобщ = a × S + 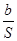,                                    (1.10)

 

где   а = 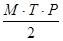,   b = Q K.

Функция суммарных затрат имеет минимум в точке, в которой ее первая производная по S равна нулю, а вторая производная больше нуля. Найдем первую производную для Собщ:

 

Собщ = (а S + ),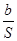

Собщ = a - 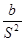.                                               (1.11)

 

Найдем значение S, обращающее производную целевой функции в ноль:

a - 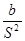 = 0,

откуда

S = .                                                 (1.12)

 

Подставляя в выражение (1.12) значения a и b, получим формулу (1.13), позволяющую рассчитать оптимальный размер заказа, которая в теории управления запасами известна как формула Уилсона:

 

S = 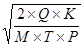.                                            (1.13)

 

Рассмотрим порядок расчета оптимальных значений остальных управляемых параметров:

- оптимальный размер затрат за период Т на создание запаса, С

 

Сопт.зак = K ;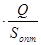

Cопт.зак = ;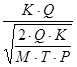

Cопт.зак = .                     (1.14)

- оптимальный размер затрат за период Т на хранение запаса, Сопт.хран:

 

Сопт.хран = M ;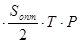

Сопт.хран = ;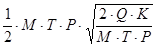

Сопт.хран = .                                (1.15)

 

- минимальный (оптимальный) размер общих затрат за период на создание и хранение запаса Смин.общ:

 

Смин.общ. = Сопт.зак. + Сопт.хран. = . (1.16)

 

Из формул (1.14) и (1.15) следует, что в точке минимума общих затрат затраты на создание запаса за период равны затратам на хранение запаса (за этот же период). Отсюда следует вывод, имеющий существенное практическое значение: если в течение периода затраты, связанные с созданием запаса были равны затратам на их хранение, то, значит, товары закупались оптимальными, то есть правильными по размеру партиями.

- оптимальный размер среднего значения текущего запаса:

 

Зопт.тек.ср. = 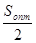.                                  (1.17)

 

- оптимальное количество заказов за период (частота завоза):

 

Nопт = 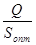.                                          (1.18)

 

- оптимальный период между поставками:

 

tопт = .                                           (1.19)

Полученное значение периода между поставками имеет годовое измерение год/заказ, то есть промежуток между заказами измеряется в годах. На практике период между поставками удобнее измерять в месяцах или днях. Расчетная формула при этом имеет вид: [3, с. 337-348]

 

tопт = .                                     (1.20)

 

Определить точный уровень необходимых резервных запасов в условиях нестабильности сроков реализации заказов, изменчивого спроса на товары и материалы достаточно сложно. Для нахождения удовлетворительных решений проблем, связанных с резервными товарно-материальными запасами, необходимо использовать моделирование или имитацию различных сценариев.

Поскольку на предприятиях различных отраслей создание товарно-материальных запасов определяется той специфической ролью, которую они играют в процессе выпуска продукции, то объяснимы и различия в подходах к политике капиталовложений в данной области и к определению приоритетности задач, решаемых в ходе производства. Например, на некоторых предприятиях народного хозяйства основной задачей является контроль за сырьем, в других — за готовой продукцией. [5]