Особенности мышления в младшем школьном возрасте

В этот период развиваются, перестраиваются мыслительные процессы. Появляются логически верные рассуждения. Тем не менее, операции в основном конкретные, с наглядным материалом. Основной вид мышления в младшем школьном возрасте – образное мышление [11, с. 276-277].

В конце младшего школьного возраста появляются индивидуальные различия. Выделяются:

1) дети-теоретики, которые легко решают учебные задачи в учебном плане;

2) дети-практики, которым нужны опора на наглядность и практические действия;

3) дети-художники с ярким образным мышлением.

В процессе обучения у младших школьников формируются понятия, в том числе и научные, которые оказывают важное влияние на становление словесно-логического мышления. Научные понятия не возникают на пустом месте. Для того чтобы лучше усвоить их, дети должны иметь развитые житейские понятия. Житейские понятия - это нижний понятийный уровень; научные понятия - верхний. Научные понятия отличаются осознанностью и произвольностью.

"Житейские понятия прорастают вверх через научные; научные понятия прорастают вниз через житейские".

Л.С. Выготский [2, с. 261]

Психолог Л.С. Выготский [20, с. 70] отмечал интенсивное развитие интеллекта в младшем школьном возрасте. Развитие мышления приводит, в свою очередь, к качественной перестройке восприятия и памяти, их превращению в регулированные, произвольные процессы.

Ребенок в 7-8 лет обычно мыслит конкретными категориями. Затем происходит переход к стадии формальных операций, которая связана с определенным уровнем развития способностей к обобщению и абстрагированию. К моменту перехода в среднее звено школьники должны научиться самостоятельно рассуждать, делать выводы, сопоставлять, сравнивать, анализировать, находить частное и общее, устанавливать простые закономерности.

Особую роль в формировании у учащихся младших классов понятий играет работа над выделением признаков, объектов. Важно научить детей видеть в объекте не только яркие, внешние признаки (которые сами бросаются в глаза), но и находить существенные признаки, без которых он не может быть подведен под данное понятие, которые выражают его сущность, отличают от других.

Критерием овладения понятием является умение правильно оперировать этим понятием, использовать при построении суждений, умозаключений, а также при образовании новых понятий. Третьеклассники должны уметь соотносить объемы понятий, устанавливать иерархию понятий, отношение понятий.

На начальном этапе учащиеся при обосновании своей точки зрения указывают на факты или аналогии. В дальнейшем они овладевают умением проводить обоснованное доказательство, подбирать аргументы.

Формирование понятийного мышления идет через развитие мыслительных операций: анализ, синтез, сравнение, обобщение, классификацию [21, с. 8].

1) Анализ - мыслительная операция, представляющая собой мысленное расчленение целого на его составные части, отдельные признаки.

Аналитическая деятельность младших школьников развивается от анализа отдельных предметов, явлений, процессов, объектов к анализу отношений между ними, что является основой понимания учащимися явлений окружающего мира. Дети овладевают умением выделять и устанавливать такие связи между понятиями, как порядок следования, противоположность, часть и целое, функциональное отношение, причинно-следственные отношения. Проще находить связь от причины к следствию, нежели наоборот, анализировать самые различные причины, которые приводят к указанному факту.

2) Синтез - операция, обратная анализу, представляет собой мысленное объединение частей предмета, отдельных признаков, притом признаков существенных, в единое целое.

 «Анализ и синтез, - писал С.Л. Рубинштейн [16, с. 73], - «общие знаменатели» всего познавательного процесса. Они относятся не только к отвлеченному мышлению, но и к чувственному познанию и восприятию».

3) Сравнение - мыслительная операция, представляющая собой установление сходства или различия предметов по существенным или несущественным признакам.

В процессе обучения у детей совершенствуются умения проводить сравнения. К третьему классу дети выделяют больше признаков, чаще сравнивают по существенным признакам, находят не только различия, но и сходства, многие могут самостоятельно составлять план сравнения.

Младшему школьнику при сравнении мало известных предметов легче найти различия, а при сравнении хорошо известных ему - сходства.

4) Классификация - распределение объектов по классам, при котором каждый класс имеет свое постоянное место.

Классификацию проводят только по одному основанию. Произведенная классификация по существенным признакам - основная, по несущественным - вспомогательная.

5) Обобщение - объединение существенных и несущественных признаков, связей, отношений, предметов и явлений.

Развитие навыков обобщения идет от широкого (например, растения) ко все более дифференцированному (например, комнатные растения) [21, с. 8-9].

 

1.4. Развитие логического мышления

младших школьников

Мышление особенно интенсивно развивается в младшем школьном возрасте, когда ребенок начинает активно осваивать окружающую действительность, приобретать новые знания, а также решать проблемные задачи в процессе учебной деятельности. Поэтому в младшем школьном возрастенеобходимо уделятьразвитию мышления ребенка особое внимание. В процессе учения ребенок усваивает научные знания и основы научно - теоретического мышления, которое, в свою очередь, предполагает способность к решению проблемных задач в уме, пользуясь знаниями, выраженными в понятиях, суждениях, умозаключениях, которые составляют основу словесно-логического мышления. Поэтому для успешного осуществления учебной деятельности в младшем школьном возрасте особое внимание должно быть уделено развитию словесно-логического мышления, благодаря которому ребенок будет интенсивно изучать и осваивать окружающую действительность.

    Процесс открытия новых знаний происходит путем сложной работы, и в этом процессе существенную роль играют и практическое, и теоретическое образное мышление. Поэтому следует развивать логическое мышление в комплексе с другими видами мышления.

Задача развития мышления стоит перед преподавателем на каждом уроке.

Логическое мышление можно и нужно развивать различными способами. Систематическое изучение науки логики и ее элементов - один из наиболее эффективных способов развития логического мышления [4, с. 3].

Логическое мышление можно развивать на уроках русского языка, когда при изучении какого-либо нового правила проводится наблюдение над группой слов, дети выявляют особенности этих слов, проводят сравнение, классификацию, обобщают и ограничивают понятия, строят суждения, проводят умозаключения.

На уроках природоведения развивается умение обобщать и классифицировать, используя содержательный материал предмета и естественные классификации.

На уроках математики развивается умение классифицировать, сравнивать, обобщать, проводить умозаключения (доказательства).

На уроке труда дети учатся конструировать различные предметы из природных и иных материалов.

    Одним из способов развития логического мышления является изучение темы "Моделирование". В явном виде она изучается на уроках информатики, но модели есть и на других предметах: на уроке русского языка - схемы слогов; на уроках окружающего мира - глобус, карта; на математике - схема анализа задачи.  

    В учебнике А.А. Плешакова «Природоведение» для 3 класса представлено очень много моделей.

    Например, модели Солнца и планет, глобус, модель смены дня и ночь, модель смены времен года, карта полушарий, модель охраны водоемов, модель круговорота веществ в почве.

Информатика в начальной школе представлена с 2002/03 учебного года как отдельный предмет, обладающий собственной методикой изучения, имеющий свою структуру и содержание, неразрывно связанные с минимумом содержания предмета информатика и информационные технологии основной школы. Обучение информатике во 2-4 классах рекомендуется проводить учителям начальной школы.

Цели обучения информатике в начальной школе: формирование первоначальных представлений о свойствах информации, способах работы с ней, в частности, с использованием компьютера.

Среди задач обучения информатике в начальной школе:

-познакомить школьников с основными свойствами информации, научить приемам организации информации и планирования деятельности, в частности учебной, при решении поставленных задач.

Линии обучения информатике в начальной школе соответствуют линиям основной школы, но реализуются на пропедевтическом уровне.

 

1.5. Изучение темы "Моделирование" как способ развития логического мышления младших школьников

Понятие моделирования

Наиболее важные и значимые общеобразовательные цели информатики — установление и усиление межпредметных связей, создание условий для восприятия и понимания информационных процессов в обществе, природе, познании — формирование у учащихся информационной картины мира.

Каждой научной дисциплине свойственно свое особое сочетание формализованных и неформализованных методов моделирования явлений, процедур доказательства и объяснения. Информатика легко преодолевает межпредметные границы.

Некоторые думают, что использование моделей началось недавно. Однако само по себе моделирование старо как мир. Оно появилось тогда, когда человечество осознало свое место в окружающем мире и стало стремиться к пониманию и изменению его [6, с. 4].

Объект - любой материальный предмет, явление, событие, процесс, который требуется изучить или описать.

О том, что определить понятие «модель» не так уж просто, можно судить по тем формулировкам, которые приведены в школьных учебниках.

«Модель – упрощенное представление о реальном объекте» [8 и 9, с. 15 и с. 292].

«Модель – это упрощенное подобие реального объекта. Всякая модель воспроизводит только те свойства оригинала, которые понадобятся человеку при его использовании» [6, с. 126].

«Модель является представлением объекта в некоторой форме, отличной от формы его реального существования» [7, с 149].

Модель - новый объект, который отражает некоторые стороны изучаемого объекта, существенные, с точки зрения цели моделирования.

Замена одного объекта (процесса или явления) другим, но сохраняющим все существенные свойства исходного объекта (процесса или явления), называется моделированием [2, с. 126].

Человек издавна использует моделирование для исследования объектов, процессов, явлений в различных областях. Результаты этих исследований служат для определения и улучшения характеристик реальных объектов и процессов; для понимания сути явлений и выработки умения приспосабливаться или управлять ими; для конструирования новых объектов или модернизации старых. Моделирование помогает человеку принимать обоснованные и продуманные решения, предвидеть последствия своей деятельности.

Компьютерное и некомпьютерное моделирование учебных и реальных объектов, ситуаций и процессов в повседневной жизни и в рамках школьных предметов ставит учащегося в активную позицию исследователя, позволяет самостоятельно открывать законы и явления.

Развитие навыков построения моделей способствует решению задачи, имеющей общеобразовательную ценность, а именно развитию системного и логического мышления. Ведь процесс построения моделей требует помимо специальных знаний еще и развитого логического мышления. И наоборот, решение задач по моделированию процессов и явлений развивает мыслительную деятельность учащихся.

Под развитием мышления учащихся в процессе обучения психологи понимают формирование и совершенствование всех видов, форм и операций мышления, выработку умений и навыков по применению законов мышления в познавательной и учебной деятельности, а также умений осуществлять перенос приемов мыслительной деятельности из одной области знаний в другую.

Таким образом, развитие мышления включает в себя:

1. Развитие всех видов мышления (наглядно-действенного, наглядно-образного, абстрактно-логического) и одновременно стимуляцию процесса перерастания их из одного вида в другой.

2. Формирование и совершенствование мыслительных операций.

3. Развитие умений:

Ø выделять существенные свойства предметов и абстрагировать их от несущественных;

Ø находить главные связи и отношения предметов и явлений реального мира;

Ø делать правильные выводы из фактов и проверять их;

Ø доказывать истинность своих суждений и опровергать ложные умозаключения;

Ø раскрывать сущность основных форм правильных умозаключений (индукции, дедукции и по аналогии);

Ø излагать свои мысли определенно, последовательно, непротиворечиво и обоснованно.

4. Выработку умения осуществлять перенос операций и приемов мышления из одной области знания в другую; прогнозирование развития явлений и умение делать выводы.

5. Совершенствование умений и навыков по применению законов и требований формальной и диалектической логики в учебной и во внеучебной познавательной деятельности учащихся.

В процессе построения модели учащиеся выделяют существенные части моделируемой системы, исследуют свойства этих объектов, находят связи между ними, проводят эксперименты и анализируют результаты моделирования. Практически все перечисленные выше процессы мыслительной деятельности прослеживаются при решении задач на составление моделей, при работе с моделями (анализе, построении).

 

Умение выделять необходимую информацию и организовывать ее в структуру — важнейшее качество человеческого интеллекта [22, с. 2].

Говоря о моделировании, надо отметить такое понятие как «системный анализ» [18, с. 114], основы которого заложил русский ученый, философ, экономист и врач Александр Александрович Богданов (1873 – 1928).

Он предположил, что в вопросах организации различных больших систем в природе, обществе, технике есть много общего, и нашел это общее (системный эффект, понятия обратной связи, управляющей и управляемой систем…).

Сила системного подхода в том, что самые разные системы окружающего мира можно изучать одинаковыми методами.

Система – организованное множество элементов любой природы, как-то связанных друг с другом и функционирующее во имя исполнения общих целей [18, с. 114].

Системное мышление – это мышление, строго учитывающее все положения системного подхода: всесторонность, взаимоувязанность, целостность, многоаспектность, учет влияния всех значимых для данного рассмотрения надсистем, систем, подсистем и связей между ними ( в отличие от детского, «узкого», синкретического мышления) [18, с. 115]. 

Одной из основных процедур системного анализа является построение хорошей модели реальной системы или ситуации для последующего адекватного изучения. Моделирование заключается в том, что создаются упрощенные копии, схемы, образы, заменители или аналогии, которые и называют моделями.

А. Эйнштейн [18, с. 128] высоко ценил умение моделировать: «осознание того, что наше сознание оперирует теоретическими моделями реальности, а не самой реальностью, является важнейшей особенностью современного научного подхода».

Моделирование – это прежде всего умение выделить главное.

Модели должны быть по возможности простыми, однако включать все самые главные части исследуемой системы (оригинала), самые главные функции и самые главные связи, внутрисистемные и внешние [18, с. 128-129].

Шаги моделирования [18, с. 130]:

а) Понять задачу (оригинал);

б) Найти главные части и связи и построить модель задачи;

в) Провести исследование модели;

г) Перенести результаты исследования модели на оригинал.

Подобная деятельность имеет место не только тогда, когда требуется некую жизненную задачу «подогнать» под ту или иную науку. Любой из нас постоянно решает какие-нибудь жизненные задачи. Прежде чем решать задачу, мы стараемся взвесить имеющуюся у нас информацию, выбрать из нее существенную. И только затем, когда в задаче станет более или менее ясно, из чего исходить и на какой результат рассчитывать, мы приступаем к решению задачи. Иногда описанный процесс называют «уяснением задачи»; фактически же речь идет о замене исходной жизненной задачи ее моделью [14, с. 49].

Как теперь видно, мы имеем дело с некой деятельностью, которая не связан ни с какой конкретной научной областью. Ее рассмотрение, изучение и, возможно, обучение ей, является прерогативой информатики, которая изучает общие закономерности информационных процессов. В данном случае речь идет о такой деятельности информационной системы как моделирование.

Человек обычно не замечает своей деятельности по созданию моделей – настолько она для него естественна. Подобно мольеровскому Журдену, с удивлением узнавшему, что всю жизнь он говорит прозой, многие люди воспринимают как откровение осознание того, что они мыслят исключительно моделями. Это, с одной стороны, облегчает создание у учащихся мотивации к изучению моделирования, поскольку у них не возникает ощущения чего-то совершенно чуждого, насильно привносимого в обучение; с другой стороны, может порождать определенные трудности, ибо создает иллюзию простоты, хотя на самом деле и само понятие модели, и тем более освоение навыков по построению моделей весьма нетривиальны.

Модель всегда описывает моделируемый объект не полностью, но при правильно выбранных частях и связях, для четко ограниченных областей и условий применения, модель описывает объект достаточно полно и правильно.

Модель может быть информационной (графической, вербальной, математической, образной) и материальной - вещественной.

Один и тот же объект, в зависимости от целей исследований, может иметь разные модели. Например, в игре с куклами моделью человека является кукла, а при испытании парашюта моделью человека является мешок с песком (100 кг), при испытании противоударных средств в автомобиле моделью человека является ватный макет с большим числом датчиков…

Логической основой моделирования является аналогия.

Под аналогией понимают умозаключение, в котором на основании сходства двух объектов в некоторых признаках и при наличии дополнительного признака у одного из них делается вывод о наличии такого же признака у другого объекта [17, с. 98-99].

В описании сути понятия «аналогия» термин «объект» используется в широком смысле: им может быть реальный предмет, модель, рисунок, числовое или буквенное выражение, задача и так далее. В качестве признаков могут выступать свойства объектов, отношения между ними, способы деятельности и так далее.

Широко используется аналогия в обучении математике младших школьников. Это происходит при изучении свойств объектов, отношений между ними и действий с ними [17, с. 99].

Посредством аналогии осуществляется перенос информации с одного предмета (прототип) на другой (модель).

 

1.5.2. Изучение темы "Моделирование" на уроке информатики в начальной школе

На уроках информатики способом развития логического мышления в числе прочих является изучение темы "Моделирование". Такие логические операции, как абстрагирование, обобщение, классификация, теоретический анализ, анализ отношений понятий (аналогии), используются при моделировании и анализе моделей, а изучение темы "Моделирование", в свою очередь, способствует формированию этих операций. Моделирование помогает понять взаимосвязи явлений и объектов. К тому же модель – это наглядный материал, с помощью которого детям легче будет усваивать информацию, делать выводы и обобщения.

Модель позволяет уменьшить уровень абстракции, когда это нужно, также позволяет постепенно увеличивать уровень абстракции (рисунок – точки – схема) для того, чтобы сделать абстрактные понятия и рассуждения понятными для детей (например, графы).

Навыки работы с моделями, которые школьники получат на уроках информатики (анализ моделей, поиск сходных и различных свойств, построение моделей), могут быть применены при изучении других предметов. Как правило, детям уже предлагаются готовые модели, которые должны бы им помочь. Однако зачастую ребенок не понимает смысла модели, не может правильно использовать модель при решении задач (на уроке математики), применении правил (на уроке русского языка), запоминании каких-либо сведений (на уроке окружающего мира). Поэтому вместо помощи в учебе модель создает дополнительные трудности: ребенку нужно усвоить и содержание новой темы (например, в курсе математики – решение задач на движение), и правила работы с моделью (с помощью которой решается эта задача). Такая «двойная проблема» не дает ребенку научиться осознанно применять модели и, с другой стороны, создает препятствия и для усвоения содержательного материала. Например, задачи на движение многие дети так и не могут научиться решать – и, не в последнюю очередь, из-за того, что «запутываются» в моделях.

Преимущество урока информатики как раз и состоит в том, что работа с моделями строится:

- постепенно, от простого к сложному (дидактический принцип последовательности);

- на содержательном материале, который понятен детям (принцип доступности);

- с учетом всех требований логики как основы моделирования (принцип научности);

- целенаправленно изучая каждый компонент моделирования и его особенности.

В компьютерном курсе информатики моделирование может быть представлено в среде графического редактора, который является удобным инструментом для построения геометрических моделей. В нем мы создаем графические объекты – рисунки. Любой рисунок, с одной стороны, является моделью некоторого оригинала (реального или мысленного объекта), а с другой стороны, - объектом среды графического редактора [6, с. 4].

Часто объект, подлежащий моделированию, можно разбить на более мелкие детали. Дом состоит из кирпичей или строительных блоков, механизм – из отдельных узлов. Если разработать набор типовых деталей, то на его основе можно создавать разные объекты. Такая деятельность получила название конструирования.

Конструирование – один из способов моделирования. Оно предполагает разработку совместимых типовых элементарных объектов (деталей) и создание более сложных объектов из этих деталей [6, с. 12]. Воплощением конструирования сейчас является конструктор «Лего».

Алгоритмические модели представлены в компьютерном курсе информатики программой «Лого».

Рассматривая бескомпьютерные курсы обучения информатике, нужно отметить тетради Алексея Львовича Семенова и Александра Владимировича Горячева. Эти два курса рекомендованы Министерством Образования РФ (Методическое письмо по вопросам обучения информатике в начальной школе. См. Приложение № 1).

В тетрадях А.Л. Семенова для начальной школы тема «Модели» отсутствует, но это понятие вводится скрыто через такие понятия, как «деревья», «цепочки» и другие.

Например, в тетради для 2 класса на стр. 25 в цепочке выражена одна из линий московского метро. Опираясь на ее графическое изображение в виде «цепочки», учащиеся определяют истинность утверждений, помещенных рядом.

В задании на стр. 16 изображены дети, стоящие в очереди за мороженым. Учащиеся должны подобрать имя каждому ребенку в очереди и продавщице и написать имена в окнах. Затем дети должны записать имена детей в окнах таким образом, чтобы данные утверждения были истинными.

«Цепочки» моделируют последовательность расположения определенных объектов.

В тетради для 3 класса на стр. 20 изображен в виде «дерева» фрагмент генеалогического дерева русских князей. Это «дерево» является графической моделью родовых связей русских князей.

Также в тетрадях представлены алгоритмы и исполнители, которые моделируют определенную последовательность действий.

В тематическом планировании учебного материала по программе «Информатика» (2 класс) в разделе «Теоретическая информатика» представлены следующие темы, связанные с моделированием:

1) Построение объекта по заданным свойствам.

2) Достраивание разных объектов до одинаковых.

3) Выделение объекта по свойствам или образцу.

4) Выделение пары объектов по заданным свойствам.

5) Выделение группы объектов, каждый из которых обладает заданным свойством.

6) Простейшие операции с информационными объектами.

7) Опыт создания информационных объектов (рисунок, текст, звук).

8) Опыт фиксации (записи) информационных объектов, конструирования информационных (виртуальных и материальных) объектов.

В тетрадях А.В. Горячева в числе прочих рассматриваются такие темы, как «Отличительные признаки» и «Графы».

Тема «Графы» вводится уже в IV четверти 1 класса. Ее цель - познакомить детей с понятием «графы» и научить их решать некоторые задачи с помощью графов.

Вот пример задания с использованием графов.

Стр. 14, № 25: От каморки папы Карло до кукольного театра ведет одна дорога, а от кукольного театра в школу – две. Сколько различных путей от каморки до школы, если Буратино хочет обязательно зайти в кукольный театр?

 

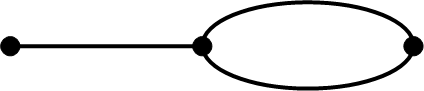
В тетради понятие «графы» не дается. Его определение есть в методических рекомендациях, и учитель вводит его сам.

Графы – точки, соединенные линиями [5, с. 78].

Точки – вершины, а линии – ребра.

В методических рекомендациях также даны различные игры, которые можно проводить с детьми по данной теме.

Одна из таких игр - «Составь меню» [5, с. 82].

Учитель рисует на доске граф:

Щи          Борщ                       Суп

Черный хлеб                      Белый хлеб

 

Вызванные к доске дети должны записать все варианты:

ЧЩ, ЧБ, ЧС и так далее.

Тема «Отличительные признаки» вводится во II четверти 3 класса.

В тетради на стр. 4 представлено следующее задание, которое называется «Загадки».

Рыба
состав	действия
чешуя глаза плавники	молчит плавает ныряет

 

Действия	Такие же действия
молчит плавает ныряет	камень корабль водолаз

 

Загадка: Не камень – а молчит, не корабль – а плавает, не водолаз – а ныряет.

Затем детям предлагается самим заполнить таблицу и составить на ее основе загадку.

В пособии Е. Челак, Н. Конопатовой "Развивающая информатика" для 2 класса рассматривается общее понятие модели и графические модели. В этом курсе присутствует тема «Формализация и моделирование», которая изучается каждый год обучения. Она включает в себя следующие разделы: Объект. Имя, признаки, действия. Части объекта. Модель. Количество моделей одного объекта. Виды моделей.

Детям предлагаются такие задания, как:

1. "Раскрась картинку одним карандашом. Дай имя объекту. Подчеркни его существенные признаки (нарисован мяч)".

2. Нарисуй графическую модель компьютера. Опиши его признаки и подчеркни среди них существенные.

3. Создай модель-схему твоего выходного дня.

Кроме вышеперечисленных, существует программа по предмету «Информатика» (для 2-4 классов). Авторы: Д.В. Аликин, А.Д. Гетманова, Е.В. Кузьмина.

По этой программе в 4 классе теме «Моделирование» уделяется 12 часов [1, с. 8].

Тема «Моделирование» направлена на знакомство учащихся с основными понятиями, связанными с моделированием и созданием моделей для информационной деятельности.

Разделы темы:

1. «Первое знакомство с моделями».

2. «Виды моделей».

3. «Моделирование на графах».

Содержание темы «Моделирование» (см. Приложение № 2).

 

Глава 2