 |
Главная |
Иррациональные уравнения с параметрами
|
из
5.00
|
Существует несколько способов решения иррациональных уравнений с параметрами. Познакомимся с ними, разобрав следующий пример.
Пример. В зависимости от значений параметра  решить уравнение
решить уравнение
 (1)
(1)
Решение. Решим уравнение (1) пятью способами, которые необходимо знать, ибо наряду с другими подходами они могут быть использованы и при решении иных типов уравнений.
Способ 1. Уравнение (1) равносильно системе

или системе
 (2)
(2)
Решая уравнение из системы (2), находим

 (3)
(3)
откуда следует, что при  уравнение (1) имеет одно решение
уравнение (1) имеет одно решение  . Если
. Если  , то
, то 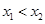 , и тогда уравнение (1) будет иметь два решения при тех значениях параметра
, и тогда уравнение (1) будет иметь два решения при тех значениях параметра  , при которых совместна система
, при которых совместна система
 ,
,
т.е. при 
Уравнение (1) будет иметь только один корень  , если
, если  , а
, а  . В этом случае решая систему
. В этом случае решая систему

приходим к выводу, что  .
.
Замечая теперь, что при  дискриминант уравнения системы (2) отрицателен, получаем
дискриминант уравнения системы (2) отрицателен, получаем
Ответ: если  , то решений нет;
, то решений нет;
если  , то
, то  ;
;
если  , то
, то  ;
;
если  , то
, то  .
.
Способ 2. Возведя обе части уравнения (1) в квадрат, получим уравнение из системы (2), корни которого задаются формулами (3). Но здесь надо иметь в виду, что при возведении обеих частей уравнения (1) в квадрат могли появиться посторонние корни.
Поэтому при данном способе решения необходимо произвести проверку. Так, подставляя корень  в исходное уравнение, придем к соотношению
в исходное уравнение, придем к соотношению
 ,
,
откуда  .
.
Если же подставить корень  в уравнение (1), то придем уже к отношению
в уравнение (1), то придем уже к отношению  , и, таким образом,
, и, таким образом,  .
.
Учитывая теперь, что при  корней нет, а при
корней нет, а при  имеем
имеем  , получаем тот же ответ, что и при первом способе решения.
, получаем тот же ответ, что и при первом способе решения.
Способ 3. Если воспользоваться геометрическим смыслом квадратного трехчлена, то, обращаясь к равносильной уравнению (1) в системе (2), приходим к выводу, что уравнение (1)будет иметь корни  и
и  в том случае, когда корни квадратного трехчлена
в том случае, когда корни квадратного трехчлена  не меньше
не меньше 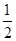 . Аналитически соответствующие условия записываются в виде системы
. Аналитически соответствующие условия записываются в виде системы
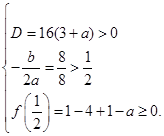
Решая эту систему, находим, что  .
.
При  уравнение (1) имеет решение
уравнение (1) имеет решение  .
.
Если же  , т.е.
, т.е.  , то уравнение (1) будет иметь один корень
, то уравнение (1) будет иметь один корень  . При
. При  решений нет.
решений нет.
Способ 4. Рассмотрим графики функций
 и
и 
заданных соответственно левой и правой частями уравнения (6.1).

Абсциссы точек пересечения этих графиков и будут решениями уравнения (1). При  графики не пересекаются (см. рис. 6.1) и значит уравнение (1) решений не имеет.
графики не пересекаются (см. рис. 6.1) и значит уравнение (1) решений не имеет.
При  графики касаются и уравнение (1) имеет один корень
графики касаются и уравнение (1) имеет один корень  .
.
При  уравнение (1) будет иметь корни
уравнение (1) будет иметь корни  и
и  , определяемые формулами (3) (см. рис. 6.2).
, определяемые формулами (3) (см. рис. 6.2).

При  графики функций
графики функций  и
и  пересекаются в одной точке, и значит уравнение (1) имеет одно решение
пересекаются в одной точке, и значит уравнение (1) имеет одно решение  (см. рис. 6.3)
(см. рис. 6.3)

Способ 5. Перепишем равносильную уравнению (1) систему (2) в виде

Построив тогда в плоскости  график функции
график функции  при условии
при условии  (см. рис. 6.4), мы приходим к выводам, полученным ранее четырьмя рассмотренными способами.
(см. рис. 6.4), мы приходим к выводам, полученным ранее четырьмя рассмотренными способами.

Ответ: если 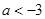 , то решений нет;
, то решений нет;
если  , то
, то  ;
;
если  , то
, то  ;
;
если  , то
, то  .
.
|
из
5.00
|
Обсуждение в статье: Иррациональные уравнения с параметрами |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

