Спектральное разложение стационарных случайных функций (процессов) в непрерывный спектр дисперсии

Перейдём к рассмотрению непрерывного спектра дисперсий стационарной случайной функции X(t).

Для этого будем рассматривать X(t) при T ® ¥. Тогда расстояния между опорными частотами 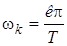 будут неограниченно уменьшаться, так как при .

При этом дискретный спектр дисперсии будет неограниченно приближаться к непрерывному, в котором бесконечно малому интервалу частот Dw_k = w_k – w_k–1 будет соответствовать элементарная дисперсия d_k(w_k).

Прежде, чем перейти к пределу, рассмотрим допредельный случай, когда интервал Dw ® 0, но ещё не равен нулю (рис. 4.6). Физический смысл мы рассматривали ранее.

Рис. 4.6. Дискретный спектр дисперсий

Примем следующие допущения:

1) по оси абсцисс (ось частот) отложим отрезки :

Рис. 4.7. Средняя плотность дисперсий

2) по оси ординат (ось дисперсий) будем откладывать среднюю плотность дисперсии – дисперсию d_k, отнесённую к величине Dw

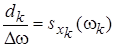                                               ,                                      (4.30)

т.е. на каждом отрезке Dw как на основании построим прямоугольник площадью d_k. Это напоминает гистограмму статистического распределения случайной величины.

Таким образом, ордината  имеет физический смысл средней плотности дисперсии и называется спектральной плотностью, т.е.

                                                ,                                       (4.31)

здесь эта величина и есть спектральная плотность процесса X(t).

Очевидно, что сумма площадей всех прямоугольников равна дисперсии D_x случайной функции X(t) в соответствии с приведённой ранее формулой:

                                           .                                 (4.32)

Ранее были получены формулы, выражающие спектральное разложение стационарной случайной функции X(t), t Î [1, T] в дискретный спектр дисперсий:

                                                                           (4.33)

                                                                                         (4.34)

                                             (4.35)

Заменим случайные величины V_k (комплексные амплитуды гармонических колебаний) случайными величинами V(w_k)×Dw, т.е.

                                                       (4.36)

Соответственно в формулах (4.34) и (4.35) заменим дисперсии d_k произведениями z_x(w_k)×Dw, т.е.

                                   ;                          (4.37)

                                          .                                 (4.38)

Преобразуем формулу (4.36) для d_k. Для этого разделим обе части формулы на величину Dw ¹ 0 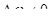 и учтём, что:

                 .        (4.39)

Формула (4.36) примет вид:

                                  .                        (4.40)

Осуществим предельный переход:

                                           .

С учётом этого формулы (4.37) и (4.41) примут вид:

                                                              (4.41)

                                                                   (4.42)

                                                                          (4.43)

                                                             (4.44)

Формула (4.43), выражающая корреляционную функцию стационарного случайного процесса через её спектральную плотность, была впервые получена в начале 30-х годов для ограниченного класса случайных процессов американским математиком, «отцом» кибернетики Норбертом Винером (1894-1964). Несколько позже эту формулу для любых стационарных случайных процессов вывел советский математик Александр Яковлевич Хинчин (1894-1959). Поэтому формулы (4.43) и (4.45), связывающие R_x(τ), S_x(w) называют формулами Винера-Хинчина.

Графический смысл предельного перехода от конечного интервала [0, T] к бесконечному при T ® ¥, Dw ® 0 выражается в том, что ступенчатая функция s_x(w_k) будет неограниченно приближаться к непрерывной функции s_x(w), которая будет изображать плотность распределения дисперсии случайных амплитуд по частотам непрерывного спектра.

Непрерывная функция s_x(w) называется спектральной плотностью стационарного случайного процесса. s_x(w) характеризует частотный состав стационарного случайного процесса X(t) и полностью определяется его корреляционной функцией R_x(τ) (4.45).

Рис. 4.8. Спектральная плотность стационарного случайного процесса

Формула (4.44) представляет собой разложение дисперсии D_x на сумму элементарных слагаемых s_x(w)dw, каждая из которых представляет собой дисперсию, приходящуюся на элементарный бесконечно малый интервал частот dw, прилежащей к точке w при (– ¥ < w < ¥).

Если рассматривать спектр дисперсии в физически возможном диапазоне частот w Î [0, ¥), то спектральная плотность S_x(w) в этом диапазоне удваивается по амплитуде с тем, чтобы площадь под кривой спектральной плотности не изменилась.

В отличие от спектральной плотности z_x(w), рассматриваемой на всём диапазоне частот, будем рассматривать спектральную плотность только для положительных частот и обозначим ее S_x(w).

С учётом этого дисперсия процесса X(t) будет вычисляться по формуле:

                                             ,                                    (4.45)

где

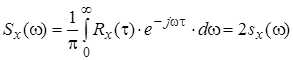                             ,                    (4.46)

                                       .                              (4.47)

На практике иногда пользуются так называемой нормированной спектральной плотностью:

                                               ,                                      (4.48)

                                               .                                      (4.49)

Так как R_x(τ) и s_x(τ) представляют собой чётные вещественные функции, то иногда формулы (4.47) и (4.48) для R_x(τ) и s_x(w) представляют в вещественной форме:

                                     ,                            (4.50)

                                    .                           (4.51)

Выражения (4.51), (4.52) получены на основе равенств

после подстановки и отбрасывания мнимых частей (слагаемых). Графически связь s_x(w) с R(t) можно представить следующим образом (рис. 4.9):

Рис. 4.9. Связь процесса со спектральной плотностью и корреляционной функцией

Чем шире спектр s_x(w), тем большие частоты представлены в X(t), т.е. тоньше структура X(t), и быстрее происходят изменения X(t) во времени.

Свойства спектральной плотности:

a) Спектральная плотность действительного стационарного случайного процесса является чётной действительной функцией аргумента w, т.е.

                        s_x(w) = – s_x(–w), Im s_x(w) = 0 – мнимая часть.

б) Дисперсия действительного стационарного случайного процесса равна интегралу от спектральной плотности этого процесса в бесконечных пределах:

                                .

в) Спектральная плотность стационарного случайного процесса – функция неотрицательная, т.е.

                                                   .

Зная спектральный состав случайного процесса, можно рационально конструировать системы различного назначения. Например, сенсорное устройство.

Рис. 4.10. Спектральная плотность сенсорного устройства

[w₁, w₂] – чувствительность сенсорного устройства.