Спектральное разложение стационарных случайных функций (процессов) в дискретный спектр дисперсии

Проведем поэтапный вывод спектрального разложения:

1) Представим стационарную случайную функцию X(t) как сумму синусоидальных функций частоты w₁, w₂, … – разложим X(t) в ряд Фурье:

                           ,                   (4.1)

или то же самое представим в комплексной форме:

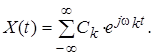                                                                                 (4.2)

Коэффициенты разложения Z_k, U_k, C_k определяются по формулам Эйлера-Фурье. В выражении (4.1) Z_k, U_k – некоррелированные центрированные случайные величины (амплитуды колебаний) с дисперсиями, одинаковыми для каждой пары случайных величин Z_k и U_k с одним и тем же индексом k:

                                           ,                                    (4.3)

где C_k – соответственно комплексная случайная величина.

Координатными функциями разложения (4.1) являются функции sin w_k t и cos w_k t при различных частотах w_k. Такое разложение называется спектральным разложением стационарной случайной функции. Частоты w_k (k = 1, 2, …) являются кратными некоторой основной частоте (первой):

                                                 ,                                          (4.4)

соответствующей периоду 2T:

                                                .                                        (4.5)

Спектральное разложение представляет собой случайную функцию X(t) в виде гармонических колебаний различных частот со случайными амплитудами (рис. 4.1). Спектр стационарного случайного процесса характеризует распределение дисперсий случайных амплитуд по частотам. Спектральное разложение (4.1) является разложением случайной функции X(t) на конечном интервале наблюдения T.

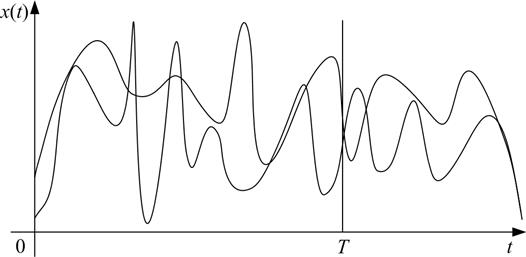
Рис. 4.1. Колебания различных частот со случайными амплитудами

Такое разложение находит широкое применение при исследовании автоматических, радиотехнических и других систем. Для исследования спектрального разложения удобно представлять его в комплексной форме.

2) Рассмотрим входящую в (4.1) гармонику частоты w_k:

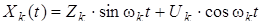                                 ,                         (4.6)

где Z_k, U_k – случайные амплитуды с характеристиками:

                 .         (4.7)

Представим Z_k(t) в комплексной форме с помощью формул Эйлера:

                        ;

                                        .                                (4.8)

Подставим выражение (4.8) в (4.6):

. (4.9)

Введём обозначения:

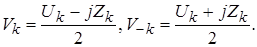                                                          (4.10)

Тогда выражение (4.9) примет следующий вид:

                                   .                          (4.11)

3) Определим вероятностные (моментные) характеристики комплексных случайных величин V_k, V_–k. Очевидно, что они центрированы:

                                           ,                                  (4.12)

так как составляющие их случайные величины также центрированы (4.7), то можно определить корреляционный момент V_k, V_–k:

    (4.13)

Так как по условию D[U_k] = D[Z_k] = D_k; U_k, Z_k – некоррелированы, определим дисперсии V_k, V_–k соответственно:

           ,

                 .       (4.14)

Таким образом

                                          .                                 (4.15)

Следовательно, как видно из выражений (4.11) и (4.14) случайные величины V_k, V_–k – амплитуды гармонического колебания X_k(t) с частотами w_k, (–w_k). А V_k, V_–k – комплексные центрированные некоррелированные случайные величины с одинаковыми дисперсиями .

4) Определим корреляционную функцию случайного процесса X_k(t):

                                ,                       (4.16)

где

                                 ;

                                   .                          (4.17)

Подставляя (4.17) в (4.16), получим:

где t₁ – t₂ = τ.

Учитывая выражение (4.14) и некоррелированность V_k, V_–k, получим:

                         .                (4.18)

Таким образом, дисперсия случайной гармоники X_k(t) при представлении её в комплексной форме делится пополам между гармоникой положительной частоты w_k и отрицательной частоты (–w_k), что представлено на рис. 4.2.

Рис. 4.2. Дисперсия случайной гармоники X_k(t)

5) Рассмотрим распределение по частотам w₁, w₂, … w_k дисперсий гармоник X_k(t), соответствующих этим частотам.

В соответствии с (4.1) и (4.11) представим случайный процесс X(t) в комплексной форме:

                            .                   (4.19)

Обозначим отрицательные частоты:

                                                                          (4.20)

Суммируем отдельно слагаемые, соответствующие положительным и отрицательным частотам:

                                              (4.21)

Заметим, что сумму отрицательных слагаемых можно выразить таким же образом, как и сумму положительных слагаемых:

                                   .                          (4.22)

С учётом (4.22) выражение (4.19) примет вид:

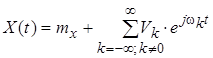                                     .                            (4.23)

Здесь мы объединили две суммы в одну, так как первая сумма содержит слагаемые с номерами k Î [1, ¥], а вторая – с номерами k Î [–¥, 1], поэтому можно рассматривать сумму членов с номерами k Î [–¥, ¥] за исключением номера k = 0. Полученное выражение (4.23) представляет собой стационарный случайный процесс X(t), составленный из случайных гармоник частоты w_k, k Î (–¥, ¥), k ¹ 0 в виде линейных комбинаций показательных функций со случайными коэффициентами.

6) Определим корреляционную функцию и дисперсию случайного процесса X(t). Корреляционная функция процесса X(t) является чётной (R_x(τ) = R_x(–τ)), т.к. процесс стационарный. Следовательно, на графике она представлена симметричной кривой (рис. 4.3).

Рис. 4.3. Корреляционная функция процесса X(t)

Свойства X(t), представленного в виде ряда Фурье:

а) при изменении t₁, t₂ от 0 до T аргумент τ = t₁ – t₂ изменяется от –T доT;

б) корреляционная функция R_xk(t₁, t₂) гармоники w_k определяется формулой (4.18);

в) Случайная функция (процесс) X(t) представляется в виде суммы гармоник различных частот (4.23);

г) Так как члены суммы (4.23) некоррелированы, то корреляционная функция R_x(t₁, t₂) равна сумме корреляционных функций слагаемых.

На основании данных свойств и с учётом выражений (4.18), (4.20) и (4.22), получим:

                                .                       (4.24)

д) Для определения дисперсии случайного процесса X(t) достаточно в выражении (4.24) представить t₁ = t₂ = t.

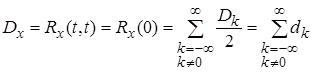                           ,                  (4.25)

где введено обозначение , т.е. ряд Фурье можно представить в виде:

                                 .                       (4.26)

Выражение (4.24) или (4.26) показывает, что частотам ±w_k соответствуют дисперсии случайных амплитуд гармоник X_k(t), т.е. корреляционная функция разложена в ряд Фурье.

Распределение дисперсии по частотам определяет так называемый спектр дисперсий стационарной случайной функции. Спектр дисперсий можно изобразить на графике в виде линейчатого спектра (рис. 4.4).

Рис. 4.4. Спектр дисперсий

На рис. 4.4 по оси абсцисс откладываются частоты w_k в соответствии с формулой (4.5), а по оси ординат – соответствующие этим частотам дисперсии.

7) Перейдём от математической абстракции к физическим процессам. Так как отрицательные частоты физически не существуют, формулы (4.24), (4.25), (4.26) можно переписать только для положительных частот w₁, w₂, … w_k. При этом дисперсии, соответствующие этим частотам, необходимо удвоить.

                                          ;                                (4.27)

                                                .                                       (4.28)

Спектр дисперсий, соответствующий только положительным частотам представлен на рис. 4.5. Формула (4.28) показывает, что дисперсия стационарного процесса X(t) равна дисперсий всех гармоник его спектрального разложения. Формула (4.26) даёт разложение корреляционной функции R_x(τ) случайного процесса X(t), t Î [0, T] в ряд Фурье, коэффициентами которого являются дисперсии d_k. А d_k вычисляются как коэффициенты ряда Фурье:

                          , k = ±1, ±2, …                 (4.29)

Рис. 4.5. Спектр дисперсий, соответствующий положительным частотам

Таким образом, X(t) и её корреляционная функция R_x(τ) разложены в ряд Фурье. Дисперсии гармоник d_k – коэффициенты ряда Фурье для корреляционной функции.