 |
Главная |
Описательные (механические) методы
|
из
5.00
|
К ним относятся: (1) метод приведения параллельных рядов,
(2) балансовый метод,
(3) графический метод,
(4) метод аналитической группировки.
Наибольший эффект достигается при комбинировании нескольких методов.
(1) Метод приведения параллельных рядов
Приводится ряд данных по одному признаку и параллельно с ним – по другому признаку, связь с которым предполагается. По вариации признака в первом и втором ряду судят о наличии связи признаков. Такой метод позволяет вывести только направление связи, но не измерить ее.
(2) Балансовый метод
Взаимосвязь может быть также охарактеризована с помощью балансов.
Пример: межрайонная связь.
 Р-н приб.
Р-н отпр. Р-н приб.
Р-н отпр.
| А | Б | В | Г | Итого отправлено |
| А | 20 | 100 | 80 | 60 | 260 |
| Б | 50 | 30 | 40 | 70 | 190 |
| В | 40 | 60 | 25 | 80 | 205 |
| Г | 100 | 50 | 90 | 35 | 275 |
| Итого прибыло | 210 | 240 | 235 | 245 | 930 |
(3) Графический метод
Может использоваться как самостоятельно, так и совместно с другими методами.
Если конкретные данные перенести на график, то полученное изображение называется полем корреляции. На оси абсцисс откладывается значение факторного признака, а на оси ординат – результативного. Каждая единица, обладающая определенным значением факторного и результативного признака, обозначается точкой.
Беспорядочное расположение говорит об отсутствии связи. Наоборот, чем сильнее связь, тем теснее точки группируются вокруг определенной линии.
(4) Метод аналитической группировки
Сначала выбираются два признака: факторный и результативный. Пол факторному признаку производится группировка, а по результативному – подсчет средних или относительных величин.
Путем сопоставления характера изменений значений факторного и результативного признака можно сделать вывод о наличии связи и ее направлении. При помощи метода аналитической группировки можно сделать вывод и о тесноте связи.
Пример: среднегодовая з/п работников-текстильщиков в 1849 г.
| Группы предприятий по числу работников | З/п в рублях |
| более 1000 | 219 |
| 501– 1000 | 204 |
| 101 – 500 | 198 |
| 51 – 100 | 188 |
| 24 – 50 | 192 |
| менее 20 | 164 |
Аналитические методы
Это основные методы изучения связи. Они делятся на непараметрические и параметрические.
Непараметрические
Их еще называют ранговыми методами. Они связаны с расчетами различных коэффициентов. Применяются как отдельно, так и совместно с параметрическими. Особенно эффективны непараметрические методы, когда необходимо измерить связь между качественными признаками. Они проще в вычислении и не требуют никаких предположений о законе распределения исходных статистических данных, т.к. при их расчете оперируют не самими значениями признаков, а их рангами, частотами, знаками и т.д.
Коэффициент Фехнера (коэффициент совпадения знаков)
| x | y |
| x1 x2 x3 . . . xn | y1 y2 y3 . . . yn |
| х = хi - х | y = yi - y |
| – + + – + + – | + + – – + – + |
Расчет основан на применении первых степеней отклонений значений признака от среднего уровня ряда двух связанных признаков.
| i = | кол-во совпадений – кол-во несовпадений |
| общее количество отклонений |
| i = | 3 – 4 | = – | 1 |
| 7 | 7 |
Коэффициент совпадения знаков может принимать значения от –1 до +1. Чем ближе значение коэффициента к |1|, тем связь более тесная. Знак коэффициента говорит о направлении, величина – о силе связи.
Коэффициенты ассоциации и контингенции
Используются для измерения связи между двумя качественными признаками, состоящими только из двух групп.

| . . . . . | . . . . . | Итого |
| . . . . . | a | b | a + b |
| . . . . . | d | c | c + d |
| Итого | a + c | b + d | a + b+ c+ d |
 Оценка
Посещение Оценка
Посещение
| Неудовлетв. | Положит. | Итого |
| Посещали | 86 | 14 | 100 |
| Не посещали | 22 | 28 | 50 |
| Итого | 108 | 42 | 150 |
 – коэфф. ассоциации;
– коэфф. ассоциации;
 – коэфф. контингенции.
– коэфф. контингенции.
Коэффициент контингенции всегда меньше коэффициента ассоциации. Связь считается подтвержденной, если  или
или  .
.
Коэффициент Спирмана (ранговый коэффициент)
Рассчитывается по следующей формуле:  .
.
| № п/п | Себестоимость |
Средняя з/п
Ранги
di = Rz - Rf
di2



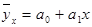
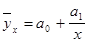

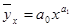
 ).
).