Метод подбора решения некорректно поставленных задач

МЕТОД ПОДБОРА. КВАЗИРЕШЕНИЯ

Возможность определения приближенных решений некорректно поставленных задач, устойчивых к малым изменениям исходных данных, основывается на исполь­зовании дополнительной информации относительно реше­ния. Возможны различные типы дополнительной инфор­мации.

В первой категории случаев дополнительная инфор­мация, носящая количественный характер, позволяет сузить класс возможных решений, например, до ком­пактного множества, и задача становится устойчивой к малым изменениям исходных данных. Во второй катего­рии случаев для нахождения приближенных решений, устойчивых к малым изменениям исходных данных, ис­пользуется лишь качественная информация о решения (например, информация о характере его гладкости).

В настоящей главе будет рассмотрен метод подбора, имеющий широкое практическое применение, метод квазирешения, а также метод замены исходного уравне­ния близким ему и метод квазиобращения. В качестве некорректно поставленной задачи мы будем рассматри­вать задачу решения уравнения

                                             Az=u                                                         (2; 0,1)

относительно z, где uÎU, zÎF, U и F—метрические пространства. Оператор А отображает F на U. Предпо­лагается, что существует обратный оператор А ^-1 , но он не является, вообще говоря, непрерывным.

Уравнение (2; 0,1) с оператором А, обладающим ука­занными свойствами, будем называть операторным урав­нением первого рода, или, короче,— уравнением пер­вого рода.

Метод подбора решения некорректно поставленных задач

2.1.1. Широко распространенным в вычислительной практике способом приближенного решения уравнения (2; 0,1) является метод подбора. Он состоит в том, что для элементов z некоторого заранее заданного подклас­са возможных решений М (МÎF) вычисляется опера­тор Az, т. е. решается прямая задача. В качестве при­ближенного решения берется такой элемент z₀ из мно­жества М, на котором невязка r_U(Az,u ) достигает мини­мума, т. е.

                                     r_U(Az₀,u ) =inf r_U(Az,u )

                                                      zÎM

Пусть правая часть уравнения (2;0,1) известна точ­но, т. е. и=u_T, и требуется найти его решение z_T. Обычно в качестве М берется множество элементов z, зависящих от конечного числа параметров, меняющихся в ограниченных пределах так, чтобы М было замкнутым множеством конечномерного пространства. Если искомое точное решение z_T уравнения (2; 0,1) принадлежит мно­жеству М, то 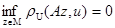 и достигается эта нижняя граница на точном решении z_T. Если уравнение (2;0,1) имеет единственное решение, то элемент z₀, минимизирующий r_U(Az,и), определен однозначно.

Практически минимизация невязки r_U(Az,и ) произ­водится приближенно и возникает следующий важный вопрос об эффективности метода подбора, т. е. о возмож­ности как угодно приблизиться к искомому точному ре­шению.

Пусть {z_n} — последовательность элементов, для ко­торой r_U(Az_n,u) ®0 при n®¥. При каких условиях можно утверждать, что при этом и r_F(z_n,z_T) ®0, т. е. что {z_n} сходится к z_T?

Это вопрос обоснования эффективности метода подбора.

2.1.2. Стремление обосновать успешность метода подбора привело к установлению общефункциональных требова­ний, ограничивающих класс возможных решений М, при которых метод подбора является устойчивым и z_n®z_T. Эти требования заключаются в компактности мно­жества М и основываются на приводимой ниже извест­ной топологической лемме.

     Лемма. Пусть метрическое пространство F отобра­жается на метрическое пространство U и Uo — образ мно­жества Fo, FoÌ F, при этом отображении. Если отобра­жение F®U непрерывно, взаимно однозначно и множест­во Fo компактно на F, то обратное отображение Uo®Fo множества Uo на множество Fo также непрерывно по мет­рике пространства F.

Доказательство. Пусть z — элементы множества F (zÎF), а u—элементы множества U (uÎU). Пусть функция u=j(z) осуществляет прямое отображение F®U, а функция z=y(u)—обратное отображение U®F.

 

Возьмем произвольный элемент u₀ из Uo. Покажем, что функция y(u) непрерывна на u₀. Предположим, что это неверно. Тогда существует такое число e₁ > 0, что для всякого d > 0 найдется элемент и ¹ из Uo, для которого r_U(и ¹, и ₀) <d, в то время как r_F(z¹,z₀)>= e₁. Здесь z=y(u¹), z₀=y(u₀) и  z¹ÎFo, z₀ÎF₀.

Возьмем последовательность {d_n} положительных чи­сел d_n , сходящуюся к нулю при п®¥. Для каждого d_n найдется элемент u_n¹ из Uo, для которого r_U(и _n ¹, и ₀) <d_n , но r_F(z_n¹,z₀)>= e₁ , где z_n¹=y(u_n¹). Очевидно, последова­тельность {u_n¹} сходится к элементу u₀. Так как z_n¹ при­надлежат компактному на F множеству Fo, то из после­довательности {z_n¹} можно выбрать подпоследовательность {Z¹n_k}, сходящуюся по метрике F к некоторому элементу z₀ ÎF. При этом z₀¹¹z₀ , так как для всякого n_kr_F(Z¹n_k,z₀)>= e₁ , следовательно и r_F(z¹₀,z₀)>= e₁ . Этой подпоследовательности {Z¹n_k} отвечает последователь­ность элементов u¹n_k= j (Z¹n_k) из Uo, сходящаяся к u¹₀= j(z¹₀) и являющаяся подпоследовательностью по­следовательности { u¹_n}. Так как последовательность  { u¹_n} сходится к и ₀ =j(z₀), то u¹₀=j(z¹₀)=u₀=j(z₀) , т. е. j(z₀)= j(z¹₀). В силу взаимной однозначности отоб­ражения F®U z¹₀=z₀, что противоречит ранее установ­ленному неравенству z¹₀¹z₀. Лемма доказана.

 Эту лемму можно сформулировать короче.

Если отображение FoàUo компакта Fo на множество Uo взаимно однозначно и непрерывно, то обратное отобра­жение UoàFo также непрерывно.

Эквивалентность этих формулировок следует из того, что замыкание F^*₀ множества Fo, компактного на F, явля­ется компактом.

Таким образом, минимизирующая последовательность {z_n} в методе подбора сходится к z_T  при nà¥, если:

а)z_T принадлежит классу возможных решений М;

б) множество М — компакт.

Пусть оператор А непрерывен и вместо точной правой части u_T мы имеем элемент u_d такой, что r_U(u_d,u_T )<= d, причем u_d принадлежит множеству AM (образу множест­ва М при отображении его с помощью оператора A) и М есть компакт. Пусть {d_n} — последовательность поло­жительных чисел таких, что d_n à0 при nàоо. Для каж­дого п методом подбора можно найти такой элемент z^d_n , что r_U(A z^d_n ,u_d)<=d_n . Элементы z^d_n будут близки к ре­шению z_T уравнения Az=u_T. В самом деле, при отобра­жении с помощью непрерывного оператора образ AM компакта М есть компакт и, следовательно, по лемме обратное отображение, осуществляемое оператором A^-1, непрерывно на AM. Так как

 

           r_U(A z^d_n ,u)<= r_U(A z_n ,u_d)+r_U(u_d,u_T),

то

           r_U(A z^d_n ,u_T)<=d_n+d=g^d_n.

Из этого неравенства и из непрерывности обратного отображения АМ à М следует, что r_F(z^d_n ,z_T)<= e(g^d_n) , причем e(g^d_n)à0 при g^d_nà0. Таким образом, при нахож­дении приближения z^d_n к z_T надо учитывать уровень по­грешности d правой части u_d.

2.1.3. На основе изложенных соображений М. М. Лав­рентьев сформулировал  понятие корректности по Тихонову. В применении к уравнению (2; 0,1) задача на­зывается корректной по Тихонову, если известно, что для точного значения u=u_T существует единственное реше­ние z_T уравнения (2; 0,1), Az_T=u_T, принадлежащее за­данному компакту М.  В этом случае оператор А ^-1 непре­рывен на множестве N=AM и, если вместо элемента u_T нам известен элемент u_d такой, что r_U( u_T, u_d)<=d и u_dÎN, то в качестве приближенного решения уравнения (2; 0,1) с правой частью u= u_d можно взять элемент z_d=A^-1u_d .  При dà0 (u_dÎN) z_d будет стремиться к z_T. Множество F₁ (F₁ Ì F), на котором задача нахождения решения уравнения (2; 0,1) является корректно постав­ленной, называют классом корректности. Так, если опера­тор А непрерывен и осуществляет взаимно однозначное отображение, то компакт М, к которому принадлежит z_T, является классом корректности для уравнения (2; 0,1). Таким образом, если задача (2; 0,1) корректна по Тихо­нову и правая часть уравнения uÎAM, то метод подбора с успехом может быть применен к решению такой задачи. На первый вопрос дан исчерпывающий ответ.

Рассмотрим задачу решения интегрального уравнения Фредгольма первого рода

                               (2;1,1)

на множестве М ₁ монотонно убывающих (возрастающих) и равномерно ограниченных функций |z(s)|<=B. Она корректна по Тихонову, так как множество M₁ — компакт в пространстве L₂.

Действительно, возьмем любую последовательность E= {z₁(s), z₂(s), .... z_n(s), ...} из M₁. Согласно теореме Хелли о выборе существуют подпоследовательность

                                   E₁ = {Zn₁ (s), Zn₂ (s), ..., Zn_k (s), ...},

последовательности Е и функция z*(s) из множества M₁, z*(s) ÎL₂, такие, что

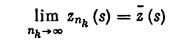
всюду, кроме, может быть, счетного множества точек разрыва функции z*(s). Из поточечной сходимости под­последовательности Е ₁ к функции z*(s) всюду, кроме, может быть, счетного множества точек, следует, как известно, сходимость подпоследовательности E₁ к функ­ции z*(s) по метрике L₂.

Таким образом, в качестве приближенного решения на множестве М₁ уравнения (2; 1,1) с приближенно извест­ной правой частью u¹ Î АМ ₁ можно брать точное решение этого уравнения с правой частью u=u¹ . Эта послед­няя задача эквивалентна задаче нахожде­ния на множестве M₁ функции, минимизирующей функ­ционал

                                 N[z,u¹]=|| A₁z – u¹ ||²_L2 .

Пусть r_U(u_T, u¹)<= d. Тогда, очевидно, в качестве при­ближенного решения уравнения (2; 1,1) можно брать функцию z_d, для которой

       || A₁z_d – u¹ ||²_L2<= d² .                                                           (2;1,2)

 

 

Если заменить интегральный оператор A₁z интеграль­ной суммой на фиксированной сетке с n узлами и обозна­чить значения искомой функции в узловых точках через z_i , то задача построения приближенного решения уравне­ния (2; 1,1) сведется к задаче нахождения конечномер­ного вектора, минимизирующего функционал N[z, и ¹ ] и удовлетворяющего неравенству (2; 1,2).

В ряде других случаев компактные классы коррект­ности можно указать эффективно, что дает возможность строить устойчивые приближенные решения.

2.1.4. В силу погрешности исходных данных элемент и может не принадлежать множеству AM. В этих условиях уравнение (2; 0,1) не имеет решения (классического) и возникает вопрос: что надо понимать под приближенным решением уравнения (2; 0,1)?

В этом случае вводится понятие квазирешения и метод подбора при условии компактности множества М позво­ляет найти приближение к квазирешению. В следующем параграфе вопрос о квазирешении рассматривается под­робнее.

 

Квазирешения

 

2.2.1.  Пусть оператор А в уравнении (2; 0,1) — вполне непрерывный. Построение устойчивого к малым измене­ниям правой части и приближенного решения уравнения (2; 0,1) по формуле

                                                            z=A^-1u           (2; 2,1)

возможно в тех случаях, как отмечалось в 2.1. , когда ре­шение ищется на компакте МÌF и правая часть уравне­ния принадлежит множеству N = AM.

Обычно не существует эффективных критериев, поз­воляющих установить принадлежность элемента и множеству N. Это приходится предполагать известным априори. В практических задачах часто вместо точного значения правой части и _T нам известно ее приближенное значение u¹, которое может не принадлежать множеству N=AM. В этих случаях нельзя строить приближенное решение уравнения (2; 0,1) по формуле (2; 2,1), так как сим­вол А^-1u может не иметь смысла.

2.2.2. Стремление устранить затруднения, связанные с от­сутствием решения уравнения (2; 0,1) при неточной правой части, привело В. К. Иванова  к понятию квазирешения уравнения (2; 0,1) — обобщению понятия решения этого уравнения.

Элемент z¹ÎМ, минимизирующий при данном и функ­ционал r_U(Az¹,и) на множестве М, называется квазиреше­нием уравнения (2; 0,1) на М,

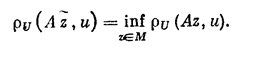
Если М — компакт, то квазирешение, очевидно, существу­ет для любого иÎU и если, кроме того, иÎAM, то ква­зирешение z¹ совпадает с обычным (точным) решением уравнения (2; 0,1). Квазирешение может быть и не одно. В этом случае под квазирешенпем будем разуметь любой элемент из множества квазирешений D.

Можно указать достаточные условия, при которых квазирешение единственно и непрерывно зависит от пра­вой части и.

Напомним определение. Пусть элемент у и множество Q принадлежат пространству U. Элемент q множества Q называется проекцией элемента у на множество Q, q=Ру, если выполняется равенство

где

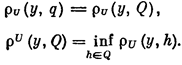
Теорема 1. Если уравнение Аz=u может иметь на компакте М не более одного решения и проекция каждого элемента uÎU на множество N = AM единственна, то квазирешение уравнения (2; 0,1) единственно и непре­рывно зависит от правой части u.

Доказательство. Пусть z¹ — квазирешение и и ¹=А z¹ . Очевидно, и ¹ есть проекция элемента u на множе­ство N = AM. По условию теоремы она определяется од­нозначно. Отсюда, в силу взаимной однозначности ото­бражения множества М на множество N, следует един­ственность квазирешения z¹.

Очевидно, что z¹ = А^-1u=А ^-1 Ри. Согласно лемме о непрерывности обратного отображения компакта (см. предыдущий параграф) оператор А^-1 непрерывен на N. Оператор проектирования Р непрерывен на U. Поэтому А^-1 P — непрерывный на U оператор и, следовательно, квазирешение z¹ непрерывно зависит от правой части и.

Таким образом, при переходе к квазирешению восста­навливаются все условия корректности, т. е. задача на­хождения квазирешения уравнения (2; 0,1) на компакте М является корректно поставленной.

Если условие единственности решения уравнения (2; 0,1) не выполнено, то квазирешения образуют некото­рое множество D элементов компакта М. В этом случае без упомянутых в теореме 1 ограничений на множество N имеет место непрерывная зависимость множества квази­решений D от и в смысле непрерывности многозначных отображений. Для случая, когда уравнение (2; 0,1) линейно, легко получить более общие результаты, содержащиеся в сле­дующей теореме .

Теорема 2. Пусть уравнение (2; 0,1) линейно, одно­родное уравнение Az=0 имеет только нулевое решение, множество М выпукло, а всякая сфера в пространстве U строго выпукла. Тогда квазирешение уравнения (2; 0,1) на компакте М единственно и непрерывно зависит от пра­вой части и.

Доказательство. Пусть z¹ — квазирешение и u¹=Az¹. Так как множество М выпукло, то в силу линей­ности оператора А множество N=AM также выпукло. Очевидно, что и ¹ есть проекция элемента и на множество N. В силу того, что сфера в пространстве U по условию теоремы строго выпукла, проекция и определяется одно­значно. Далее доказательство завершается, как в тео­реме 1.

2.2.3. Пусть F и U — гильбертовы пространства, МÎS_R — шар (|| z ||<=R ) в пространстве F и А — вполне непре­рывный линейный оператор.

В этом случае квазирешение уравнения (2; 0,1) мож­но представить в виде ряда по собственным элементам (функциям, векторам) j_n оператора А*А, где А* — опе­ратор, сопряженный оператору А.

Известно, что А*А — самосопряженный положитель­ный вполне непрерывный оператор из F в F. Пусть l₁>=l₂>=…>=l_n>=… — полная система его собственных значений, a j₁, j₂,…, j_n,…—отвечающая им полная ортонормированная система его собственных элементов (функций, векторов). Элемент А*и можно представить в виде ряда

                                                                            (2;2,2)

В этих условиях справедлива

Теорема 3. Квазирешение уравнения (2, 0,1) на множестве S_R выражается формулами:

                                                                     (2;2,3)

если

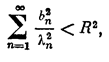                                                                                     (2;2,4)

и

 

                                                                   

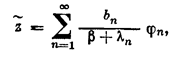
если

                                                                         (2;2,5)

           

Здесь b — корень уравнения

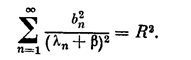                                                          (2;2,6)  

 

 

Доказательство. Квазирсшение минимизирует функционал

                                         r_U² (Az, u) == (Az — u, Az — u)                      (2;2,7)

(где (v,w ) — скалярное произведение элементов v и w из U), уравнение Эйлера для которого имеет вид

                                    A*Az=A*u.                                                        (2;2,8)

 

Решение этого уравнения будем искать в виде ряда по системе {j_n}:

 

                                                                         (2;2,9)      

 

Подставляя этот ряд в уравнение (2; 2,8) и используя разложение (2;2,2), находим с_n=b_n/l_n. Следователь­но, неравенство (2; 2,4) означает, что ||z||<R и речь идет о нахождении безусловного экстремума функциона­ла (2; 2,7). Ряд (2; 2,3) и будет решением задачи.

Если же выполняется неравенство (2; 2,5), то это означает, что ||z||>=R и надо решать задачу на услов­ные экстремум функционала (2; 2,7) при условии, что || z ||² = R². Методом неопределенных множителей Лагранжа эта задача сводится к нахождению безусловного экстремума функционала

(Аz-u, Аz-u) + b (z, z),

 

а последняя — к решению отвечающего ему уравнения Эйлера A*Az+bz=А*и. Подставляя сюда z в виде ряда (2; 2,9) и используя разложение (2; 2,2), находим

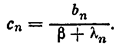
Параметр b определяем из условия || z ||² = R² , которое эквивалентно (2; 2,6).