Метод регуляризации нахождения нормального решения

 

3.3.1. Пусть z° есть нормальное решение системы

А z = и.              (3; 3,1)

Для простоты будем полагать, что прибли­женной может быть лишь правая часть, а оператор (матрица) А — точный.

Итак, пусть вместо и мы имеем вектор и, || и — и || <=d ; т. е. вместо системы (3;3,1) имеем систему

(3; 3,2)

Аz = u.

 

Требуется найти приближение z_d к нормальному реше­нию системы (3;3,1), т. е. к вектору z° такое, что z_d àz° при d à0. Отметим, что векторы u и u (один из них или оба) могут не удовлетворять классическому ус­ловию разрешимости.

Поскольку система (3; 3,1) может быть неразреши­мой, то inf ||Az-u|| = m >=0, где inf берется по всем векторам z Î Rⁿ.

Естественно искать приближения z_d  в классе Q_d  век­торов z, сопоставимых по точности с исходными данны­ми, т. е. таких, что || Az – u ||<=m+d. Но поскольку вместо вектора u мы имеем вектор u, то мы можем найти лишь

m=inf || Az – u ||.

 zÎ Rⁿ

Отметим, что из очевидных неравенств

||Az – u ||<=||Az – u || + || u – u || ,

                                                      ||Az – u ||<= || Az – u || + ||u – u ||

следуют оценки m<=m+d, m<=m+d, приводящие к не­равенству | m — m | <=d. Поэтому будем искать прибли­жение z_d к нормальному решению z° в классе Q_d векто­ров z, для которых || А z — и || < =m +2d. Отметим, что если имеется информация о разрешимости системы (3;3,1), то m = 0 и в качестве класса Q_d можно брать класс векторов z, для которых || А z — и || < = d. Класс Q_d есть класс формально возможных приближенных решений.

Но нельзя в качестве z_d брать произвольный вектор из класса Q_d, так как такое «приближение» будет неустойчивым к малым изменениям правой части уравнения (3;3,2). Необходим принцип отбора. Он естественным образом вытекает из постановки задачи. В самом деле согласно определению нормального решения искомое ре­шение z° должно быть псевдорешением с минимальной нормой. Поэтому в качестве приближения к z° естествен­но брать вектор z_d из Q_d, минимизирующий функционал

W[ z ] = ||z||² на множестве Q_d .

Таким образом, задача сводится к минимизации функ­ционала W[ z ] = ||z||² на множестве Q_d векторов z, для которых выполняется условие || А z — u || <=m +2d.

3.3.2. Пусть z_d — вектор из Q_d, на котором функционал ||z||² достигает минимума на множестве Q_d. Его можно рассматривать как результат применения к правой части u уравнения (3; 3,2) некоторого оператора R₁( u , d), зависящего от параметра d. Справедлива

Теорема 1. Оператор R₁(u, d) обладает следующи­ми свойствами:

1) он определен для всякого uÎR^m и любого d > 0;

2 ) приd à 0  z _d == R₁(u, d) стремится к нормальному решению z ° уравнения Аz=u, т. е. он является регуляризирующим для уравнения Аz=u .

3.3.3. Пусть  z_d — вектор, на котором функционал W[ z ] = ||z||² достигает минимума на множестве Q_d. Легко ви­деть из наглядных геометрических представлений, что вектор z_d лежит на границе множестваQ_d, т.е. ||Az_d - u ||=m +2d =d₁.

 Это следует непосредственно также из того, что функционал W[ z ] = ||z||² является сстабилизирующим и квазимонотонным. Стабилизирующий функционал W[ z ] называется квазимонотонным , если каков бы ни был элемент z из F₁ , не принадлежащий множеству M₀ , в любой его окрестности найдется элемент z₁ из F₁, для которого W[ z₁ ]< W[ z ], т.е. если функционал не имеет локальных минимумов на множестве F₁\ M₀.

Задачу нахождения вектора z_d  можно поставить так: среди векторов z, удовлетворяющих условию ||Az – u ||=m +2d, найти вектор z_d с минимальной нормой, т. е. минимизирующий функционал W[ z ]=||z||².

Последнюю задачу можно решать методом Лагранжа, т. е. в качестве z_d брать вектор z^a, минимизирующий функционал

М^a [z, u] = ||Az - u ||²+ a||z||²,    a>0,

с параметром a, определяемым по невязке, т. е. из ус­ловия ||Аz^a— u||=d1. При этом параметр a определяется однозначно .

3.3.4. Поскольку М^a [z, u]  — квадратичный функционал, то для любых u ÎR^m и a> 0 существует лишь один минимизирующий его вектор z^a. В самом деле, допустим,

что существуют два вектора z^a и z^a, минимизирующие его. Рассмотрим векторы z, расположенные на прямой (пространства Rⁿ), соединяющей z^a и z^a:

z = z^a + b( z^a - z^a).

Функционал М^a [z, u]  на элементах этой прямой есть неотрицательная квадратичная функция от b. Следова­тельно, она не может достигать наименьшего значения при двух различных значениях b: b = 0 (z = z^a) и b=1 (z = z^a).

Компоненты z_j^a вектора z^a являются решением си­стемы линейных алгебраических уравнений

получающихся из условий минимума функционала М^a [z, u]:

Здесь

 

Компоненты z_j^a могут быть определены и с помощью какого-нибудь другого алгоритма минимизации       функцио­нала М^a [z, u].

Вектор z^a можно рассматривать как результат приме­нения к u некоторого оператора z^a=R(u, a), завися­щего от параметра a.

Покажем, что оператор R₀(u, a) является регуляризирующим для системы (3;3,1), т. е. обладает свойствами 1) и 2) определения 2 (см. 3.1.2.). В п. 3.3.2. было сказано, что он определен для всяких u ÎR^m и a > О и, следовательно, обладает свойством 1). Теперь пока­жем справедливость свойства 2), т. е. существование таких функций a=a(d) , что векторы z^a(d) = R₀(u, a(d)) сходятся к нормальному решению z° системы (3; 3,1) при dà0. Это непосредственно следует из приводимой ниже теоремы 2.

Теорема 2( Тихонова). Пусть z° есть нормальное решение си­стемы Az= u и вместо вектора u мы имеем вектор u  такой, что ||u—u||<=d. Пусть, далее, b1(d) и b2(d) — какие-либо непрерывные на [0, d2] и положительные на (0, d2] функции, монотонно стремящиеся к нулю при dà 0 и такие, что

                                

Тогда для любой .положительной на (0, d2] функции a=a(d) , удовлетворяющей условиям

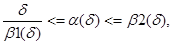
векторы z^a(d) = R₀(u, a(d))  сходятся к нормальному ре­шению z⁰ системы Az = u при dà0, т. е.

Примечание. Доказательства теорем в данном разделе опущены, т.к. основной теоретической частью работы является раздел «Метод Подбора. Квазирешения». Метод Тихонова описан из-за использования его в численном эксперименте.

 

 

ЗАКЛЮЧЕНИЕ

    Для реализации численного примера был выбран метод Тихонова решения плохо обусловленных СЛАУ. В качестве исходной была взята СЛАУ Az=u, имеющая в матричной записи вид:

Определитель матрицы коэффициентов этой системы близок к нулю – он равен 0.000125. Попробуем решить эту систему с помощью обратной матрицы:

z=A^-1u

Получим z₁=316

               z₂=-990

               z₃=832

Теперь предположим, что правая часть нам известна приближенно, с погрешностью 0.1 Изменим, к примеру, третий элемент вектора-столбца с 1 на 1.1 :

Попробуем решить новую систему также с помощью обратного оператора. Мы получаем другой результат:

              z₁=348

         z₂=-1090

         z₃=916.

Мы видим, что малому изменению правой части данной системы отвечают весьма значительные изменения решения. Очевидно, эта система – плохо обусловленная, и здесь не может идти речи о нахождении решения близкого к точному с помощью обратного оператора.

       Будем искать решение методом Тихонова. В теоретической части было показано, что целесообразно использовать регуляризирующий оператор следующего вида: (aE + A^TA)z^a=A^Tu_d , где E – единичная матрица, z^a -- приближенное нормальное решение, A^T – транспонированная исходная матрица, a -- параметр регуляризации,

u_d --  правая часть, заданная неточно. Эту задачу можно решать стандартными методами, задав предварительно функцию a=a(d) , удовлетворяющую условиям теоремы Тихонова. В моем примере это функция a(d)=d/4^d. Далее будем решать регуляризованную задачу с точностью e=0.001 ,последовательно изменяя значения a.

В качестве контр-примера можно подставить в программу любую функцию a(d) , не удовлетворяющую условиям теоремы Тихонова. Любая положительная функция монотонно возрастающая, не обладающая свойством a(d)à0 при dà0, не будет минимизировать невязку.

Текст программы приведен в приложении 1. Полная распечатка результатов приведена в приложении 2. Здесь же представлены окончательные значения на выходе из программы.

 

Приближение к нормальному решению

Z(1)= 3.47834819174013E+0002

Z(2)=-1.08948394975175E+0003

Z(3)= 9.15566443137791E+0002

 

Значение правой части при подстановке прибл. решения

U1(1)= 9.99997717012495E-0001

U1(2)= 1.00000741970775E+0000

U1(3)= 1.09948402394883E+0000

 

Значение параметра регуляризации:

 2.61934474110603E-0010

 

ПРИЛОЖЕНИЯ

Приложение 1.

Текст программы для реализации метода Тихонова на языке PASCAL

 

Uses CRT;

 

type

 

 real=extended;

 

const

 

matrixA: array[1..3,1..3] of real = ((-19/20,1/5, 3/5),

                                 (-1 ,0.1, 0.5),

                                 (-0.01 ,0 ,1/200));

One: array [1..3,1..3] of real = ((1,0,0),

                               (0,1,0),

                               (0,0,1));

U:array[1..3] of real = (1,1,1.1);

 

var

i,j,k,q:byte;

A,At,A1,A2,Ar,One1:array[1..3,1..3] of real;

delta,Det,S,alpha:real;

B,Z,U1:array[1..3] of real;

f:text;

 

Procedure TransA;

begin

for i:=1 to 3 do

for j:=1 to 3 do

    At[i,j]:=A[j,i]

end;

 

Function Koef(par1,par2:byte):real;

var

Sum:byte;

Tmp:real;

begin

  Sum:=par1+par2;

  Tmp:=1;

  for k:=1 to sum do

   Tmp:=Tmp*(-1);

  Koef:=Tmp;

end;

 

Function AlAdd(par1,par2:byte):real;

type

element=record

        value:real;

        flag:boolean;

        end;

var

BB:array[1..2,1..2] of real;

AA:array[1..3,1..3] of element;

k,v,w:byte;

N:array[1..4] of real;

P1:real;

begin

for v:=1 to 3 do

for w:=1 to 3 do begin

  AA[v,w].value:=A2[v,w];

  AA[v,w].flag:=true

end;

for v:=1 to 3 do AA[par1,v].flag:=false;

for v:=1 to 3 do AA[v,par2].flag:=false;

{ for v:=1 to 3 do begin

for w:=1 to 3 do write(AA[i,j].value:2:3,' ');

writeln

end; }

k:=1;

for v:=1 to 3 do

for w:=1 to 3 do

  begin

  if AA[v,w].flag then

   begin

    N[k]:=AA[v,w].value;

{ writeln(N[k]);}

    k:=k+1

   end;

  end;

BB[1,1]:=N[1]; BB[1,2]:=N[2];

BB[2,1]:=N[3]; BB[2,2]:=N[4];

{ writeln('alg dop',par1,par2,' ',BB[1,1]*BB[2,2]-BB[1,2]*BB[2,1]);}

AlAdd:=BB[1,1]*BB[2,2]-BB[1,2]*BB[2,1];

end;

 

Function DetCount:real;

var

  S1:real;

  z:byte;

begin

S1:=0;

for z:=1 to 3 do S1:=S1+A2[1,z]*Koef(1,z)*AlAdd(1,z);

DetCount:=S1;

end;

 

Procedure RevMatr;

begin

  for i:=1 to 3 do

   for j:=1 to 3 do

    Ar[j,i]:=Koef(i,j)*AlAdd(i,j)/DetCount;

{  for i:=1 to 3 do begin

   for j:=1 to 3 do write(Ar[i,j],' ');

   writeln;

  end;}

end;

 

Function AllRight:boolean;

begin

  writeln(f,'­Ґўп§Є Ї® 1-г н«-вг',(abs(U[1]-U1[1])));

  writeln(f,'­Ґўп§Є Ї® 2-г н«-вг',(abs(U[2]-U1[2])));

  writeln(f,'­Ґўп§Є Ї® 3-г н«-вг',(abs(U[3]-U1[3])));

  writeln(F);

  if (abs(U[1]-U1[1])<0.001) and (abs(U[2]-U1[2])<0.001) and

     (abs(U[3]-U1[3])<0.001) then AllRight:=true

     else AllRight:=false

end;

 

Function Pow(par1:real;par2:byte):real;

var

  S2:real;

  z:byte;

begin

  S2:=1;

  if par2=0 then begin

   Pow:=1;

     exit

  end

    else

      for z:=1 to par2 do S2:=S2*par1;

  Pow:=S2;

end;

 

BEGIN

  clrscr;

  Assign(f,'c:\tikh.txt');

  Rewrite(f);

  for i:=1 to 3 do

   for j:=1 to 3 do

    A[i,j]:=matrixA[i,j];

  TransA;

  Det:=0.000125;

  {----------------------------}

  for i:=1 to 3 do begin

   S:=0;

   for j:=1 to 3 do begin

     S:=S+At[i,j]*U[j];

     B[i]:=S

    end;

  end;

  {----------------------------}

  for i:=1 to 3 do

   for j:=1 to 3 do

    begin

     S:=0;

      for k:=1 to 3 do begin

       S:=S+At[i,k]*A[k,j];

       A1[i,j]:=S

      end

    end;

  {-----------------------------}

  q:=1;

repeat

  alpha:=q/pow(4,q);

  for i:=1 to 3 do

   for j:=1 to 3 do

    One1[i,j]:=One[i,j]*alpha;

  for i:=1 to 3 do

   for j:=1 to 3 do

    A2[i,j]:=One1[i,j]+A1[i,j];

  RevMatr;

  {------------------------------}

  for i:=1 to 3 do begin

   S:=0;

   for j:=1 to 3 do begin

     S:=S+Ar[i,j]*B[j];

     Z[i]:=S

    end;

  end;

  for i:=1 to 3 do begin

   S:=0;

    for j:=1 to 3 do begin

     S:=S+A[i,j]*Z[j];

     U1[i]:=S

    end

  end;

  q:=q+1;

  until AllRight;

  {------------------------------}

  clrscr;

  writeln('ЏаЁЎ«Ё¦Ґ­ЁҐ Є ­®а «м­®г аҐиҐ­Ёо');

 for i:=1 to 3 do writeln('Z(',i,')=',z[i]);

  writeln;

  writeln('‡­ 祭ЁҐ Їа ў®© з бвЁ ЇаЁ Ї®¤бв ­®ўЄҐ ЇаЁЎ«. аҐиҐ­Ёп');

  for i:=1 to 3 do writeln('U1(',i,')=',U1[i]);

  writeln;

  writeln('‡­ 祭ЁҐ Ї а Ґва ॣг«паЁ§ жЁЁ:');

  writeln(alpha);

  Close(f);

  readln;

END.

 

Приложение 2.

Распечатка результатов пересчета на каждом шаге

невязка по 1-му эл-ту 7.75620788018006E-0002

 

невязка по 2-му эл-ту 9.12970302562861E-0002

невязка по 3-му эл-ту 1.09101153877771E+0000

 

невязка по 1-му эл-ту 3.51667654246499E-0002

невязка по 2-му эл-ту 4.81631787337596E-0002

невязка по 3-му эл-ту 1.09057642915500E+0000

 

невязка по 1-му эл-ту 8.14255746519741E-0003

невязка по 2-му эл-ту 1.75271999674588E-0002

невязка по 3-му эл-ту 1.09024740493812E+0000

 

невязка по 1-му эл-ту 1.64128226088452E-0004

невязка по 2-му эл-ту 1.40420815653456E-0003

невязка по 3-му эл-ту 1.09002512985506E+0000

 

невязка по 1-му эл-ту 1.09651876415789E-0003

невязка по 2-му эл-ту 8.01044623892439E-0003

невязка по 3-му эл-ту 1.08980075500722E+0000

 

невязка по 1-му эл-ту 3.24092274239579E-0003

невязка по 2-му эл-ту 1.28969442769472E-0002

невязка по 3-му эл-ту 1.08943309314635E+0000

 

невязка по 1-му эл-ту 4.29878415191160E-0003

невязка по 2-му эл-ту 1.47864580098997E-0002

невязка по 3-му эл-ту 1.08840358157784E+0000

 

невязка по 1-му эл-ту 4.64764022304719E-0003

невязка по 2-му эл-ту 1.53489294761093E-0002

невязка по 3-му эл-ту 1.08488736141985E+0000

 

невязка по 1-му эл-ту 4.70263264899617E-0003

невязка по 2-му эл-ту 1.53524096326819E-0002

невязка по 3-му эл-ту 1.07252416252061E+0000

 

невязка по 1-му эл-ту 4.54618391386039E-0003

невязка по 2-му эл-ту 1.47935415193105E-0002

невязка по 3-му эл-ту 1.03007092553528E+0000

 

невязка по 1-му эл-ту 3.97950585276394E-0003

невязка по 2-му эл-ту 1.29378307693635E-0002

невязка по 3-му эл-ту 9.00028069734717E-0001

 

невязка по 1-му эл-ту 2.71895340473448E-0003

невязка по 2-му эл-ту 8.83742514077426E-0003

невязка по 3-му эл-ту 6.14624514462952E-0001

 

невязка по 1-му эл-ту 1.25089904346179E-0003

невязка по 2-му эл-ту 4.06552487723671E-0003

невязка по 3-му эл-ту 2.82729125073012E-0001

 

невязка по 1-му эл-ту 4.15581257891512E-0004

невязка по 2-му эл-ту 1.35064829843828E-0003

невязка по 3-му эл-ту 9.39264706989556E-0002

 

невязка по 1-му эл-ту 1.18814900667952E-0004

невязка по 2-му эл-ту 3.86149131520602E-0004

невязка по 3-му эл-ту 2.68533566153482E-0002

 

невязка по 1-му эл-ту 3.22671215741144E-0005

невязка по 2-му эл-ту 1.04868192738639E-0004

невязка по 3-му эл-ту 7.29267248287954E-0003

 

невязка по 1-му эл-ту 8.61328853146714E-0006

невязка по 2-му эл-ту 2.79931897352870E-0005

невязка по 3-му эл-ту 1.94668264668650E-0003

 

невязка по 1-му эл-ту 2.28298750498679E-0006

невязка по 2-му эл-ту 7.41970775380851E-0006

невязка по 3-му эл-ту 5.15976051172231E-0004

 

Приближение к нормальному решению

Z(1)= 3.47834819174013E+0002

Z(2)=-1.08948394975175E+0003

Z(3)= 9.15566443137791E+0002

Значение правой части при подстановке прибл. решения

U1(1)= 9.99997717012495E-0001

U1(2)= 1.00000741970775E+0000

U1(3)= 1.09948402394883E+0000

 

Значение параметра регуляризации:

 2.61934474110603E-0010