 |
Главная |
Нестационарная задача для сетки.
|
из
5.00
|
Перейдем теперь к вопросу о конструировании сеток при расчетах нестационарных задач с подвижными границами.
Пусть N – номер очередного шага по времени t,  - величина шага по временной координате t ,
- величина шага по временной координате t ,  - сетка, полученная на предыдущем шаге. Вектор
- сетка, полученная на предыдущем шаге. Вектор  содержит две пространственные координаты (х,у) и, в дискретном варианте, о котором речь пойдет в § 3, значения этих координат во всех узлах расчетной сетки.
содержит две пространственные координаты (х,у) и, в дискретном варианте, о котором речь пойдет в § 3, значения этих координат во всех узлах расчетной сетки.
Для определенности пусть рассматривается некоторая газодинамическая задача без конкретизации ее содержания. В соответствии с общепринятой схемой расщепления расчет очередного шага состоит из нескольких этапов.
На I этапе осуществляется движение границ расчетных областей. Оно обусловлено теми или иными физическими законами и конкретным распределением физических величин в окрестности границы на текущий момент времени. Абстрагируясь от них, будем предполагать, что последовательности  определяют положение границ на предыдущем шаге и превращаются в последовательности
определяют положение границ на предыдущем шаге и превращаются в последовательности  для очередного рассчитываемого шага. Очевидно можно полагать, что
для очередного рассчитываемого шага. Очевидно можно полагать, что
(2.1) 
Условимся подразумевать, что (2.1) и аналогичные равенства в дальнейшем выполнены для каждой из координат вектора  .
.
По соображениям, изложенным в [8], в качестве II этапа расчета целесообразно вычислить величины сдвига граничных узлов сетки
(2.2)  ,
,
затем по интерполяционным формулам рассчитать значения сдвига 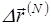 для внутренних узлов сетки и получить начальное приближение
для внутренних узлов сетки и получить начальное приближение
(2.3) 
для узлов сетки N-го шага. Граничные узлы при этом занимают правильное положение, которое при дальнейшем расчете сетки текущего шага изменяться не будет.
Обсуждение интерполяционных формул отложим до § 6.
Из них будет очевидно, что
(2.4) 
Перейдем теперь к III этапу – назначению матриц коэффициентов G для описанных выше функционалов.
Предлагается использовать для этого метрические параметры сетки, полученной на предыдущем шаге по времени:
(2.5)  .
.
Как описано выше в § 1, такое назначение будет воспроизводить сетку предыдущего шага, т.е.
(2.6)  для функционала (1.1)-(1.2),
для функционала (1.1)-(1.2),
 для функционала (1.8)-(1.9).
для функционала (1.8)-(1.9).
В силу (2.4), можно полагать, что
(2.7) 
и аналогично для второго функционала.
Конечно, строго говоря, при этом необходимо формулировать требования, которые нужно накладывать на гладкость границ области, гладкость текущей сетки и т.п. Мы их опускаем, тем более, что практически эти требования необходимо формулировать для дискретного варианта, который будет описан позже в § 3.
При хорошей обусловленности систем уравнений можно было бы полагать также, что искомые сетки  , определяемые из уравнений:
, определяемые из уравнений:
 или
или 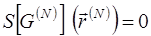 , удовлетворяют условию:
, удовлетворяют условию:
(2.8)  .
.
Это полностью решало бы проблему конструирования сеток при расчете нестационарных задач. К сожалению, на практике дело обстоит хуже. При назначении (2.5) рассматриваемые функционалы обнаруживают «равнодушие» к судьбе конструируемой сетки, поскольку для любой сетки значение функционала близко к абсолютному минимуму, отличаясь от него лишь на величину порядка  из-за отклонения граничных условий (2.1). При отсутствии обратной связи ухудшение качества сетки постепенно может приводить к необратимым последствиям, вплоть до «авостных». Поэтому назначение (2.5) необходимо корректировать.
из-за отклонения граничных условий (2.1). При отсутствии обратной связи ухудшение качества сетки постепенно может приводить к необратимым последствиям, вплоть до «авостных». Поэтому назначение (2.5) необходимо корректировать.
В работе [1] при расчете стационарных сеток (для областей с фиксированными границами) рассматривался один из возможных вариантов такой корректировки метрических параметров (см.[1], стр.25):
(2.9) 


Она гарантирует выполнение условия 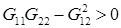 для
для 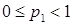 ,
,  . Оказалось, что, в силу нормировки (1.6)-(1.7), формулы (2.9) эквивалентны таким:
. Оказалось, что, в силу нормировки (1.6)-(1.7), формулы (2.9) эквивалентны таким:
 ,
,  ,
,  ,
,

При условии сохранения хорошей обусловленности для корректированной системы уравнений тоже можно надеяться на выполнение условия (2.8), если  . От вычурного вида формулы для
. От вычурного вида формулы для  можно отказаться и в качестве корректировки принять:
можно отказаться и в качестве корректировки принять:
(2.10)  ,
,  ,
,  ,
,
где p>0 – управляющий параметр. Эти формулы представляют, конечно, лишь один из возможных вариантов корректировки. Этот вариант отражает стремление «приблизить» сетку к «квазиортогональной».
Однако более эффективным оказался вариант корректировки самого функционала. Для функционала (1.1)-(1.2) с якобианом предлагается:
(2.11)  ,
,

Для функционала (1.8)-(1.9) без якобиана:
(2.12)  ,
, 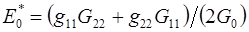
Для реализации (2.11) или (2.12) достаточно изменить формулы нормировки (1.6)-(1.7):
(2.13) 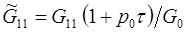 ,
,  ,
,  ,
,
сохранив  и назначение (2.5) :
и назначение (2.5) :  .
.
Интересно отметить, что при назначении (1.5) корректирующие функционалы  и
и  приобретают вид соответственно:
приобретают вид соответственно:
(2.14)  ,
, 
Первый из них рассматривался в работе [9] в качестве «функционала ортогональности», а второй – автором в работе [10] – в качестве одного из вариантов для получения «квазиортогональных» сеток. В обоих случаях их прямое использование для расчета сеток обнаружило некорректность, которую пришлось преодолевать подключением дополнительных «регуляризующих» средств. Предлагаемый вариант их реализации в качестве такого средства использует «опорные» функционалы (1.1)-(1.2) или (1.8)-(1.9), к которым они подключаются с коэффициентом  .
.
Возникает также общее предложение: использовать для корректировки опорных функционалов произвольные «хорошие функционалы» со своими управляющими коэффициентами 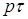 . Термин «хорошие функционалы» предполагает обеспечение хорошей обусловленности для корректированного функционала и целенаправленное воздействие на рассчитываемую сетку для обеспечения ее качества, требуемого при решении основной задачи. Обратим внимание на необходимость согласования размерности используемых функционалов по переменным (х,у).
. Термин «хорошие функционалы» предполагает обеспечение хорошей обусловленности для корректированного функционала и целенаправленное воздействие на рассчитываемую сетку для обеспечения ее качества, требуемого при решении основной задачи. Обратим внимание на необходимость согласования размерности используемых функционалов по переменным (х,у).
Отметим также, что с точки зрения размерности по t представляется целесообразным вместо управляющих коэффициентов 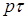 задавать для корректирующих функционалов весовые коэффициенты формулами:
задавать для корректирующих функционалов весовые коэффициенты формулами:
(2.15)  , где
, где 
В частности, например, подключение функционала, реализующего гармонические сетки, с коэффициентом  достигается заменой (2.13) на следующие формулы:
достигается заменой (2.13) на следующие формулы:

 ,
,
(2.16) 
 .
.
Дискретизация.
Следующим этапом работы по созданию алгоритма расчета сеток является переход от дифференциальной формы вариационного функционала к дискретной. Простейшим и экономным способом его реализации была бы замена дифференциальных выражений разностными в уравнениях Эйлера-Лагранжа (1.13) для функционала (1.8)-(1.9) и следствий из таких уравнений (1.14) для функционала (1.1)-(1.2). Однако, как уже отмечалось, например, в [1], мнение о том, что этот этап сводится к механической замене дифференциальных выражений разностными, является ошибочным. При такой замене могут быть утеряны важные свойства дифференциальной модели.
Для рассматриваемой задачи крайне важным является обеспечение для дискретной модели условий (2.6), т.е. тождественного равенства нулю невязок разностных уравнений, возникающих после назначения (2.5) коэффициентов G, при подстановке в эти уравнения сетки предыдущего временного шага. Нарушение этого требования в надежде, что погрешности аппроксимации окажутся достаточно малыми, может приводить к неконтролируемым значениям для скоростей узлов сетки. Гарантию достижения этой цели дает тщательная реализация специальной процедуры, известной под названием вариационного
барьерного метода. Впервые она была изложена в работе [11] для расчета гармонических сеток, хорошо известна и многократно описана.
Изложение окончательного результата, имеющего непосредственное отношение к рассматриваемым функционалам, в нужных нам обозначениях представлено в [1] на стр. 16-17. Для полноты изложения и некоторых дополнительных замечаний целесообразно его повторить.
Дискретный аналог функционала (1.1)-(1.2) записывается в виде:
(3.1)  ,
,
где суммирование производится по всем ячейкам сетки расчетной области. Обычно им присваивают «полуцелые» номера (  ). Нормирующий коэффициент на число ячеек сетки в формуле (3.1) опущен как не влияющий на дальнейший результат.
). Нормирующий коэффициент на число ячеек сетки в формуле (3.1) опущен как не влияющий на дальнейший результат.
Разностные уравнения для узла сетки с номером (n,m) имеют вид:
(3.2)  ,
, 
Для их получения достаточно рассмотреть «шаблон», в котором участвуют 4 ячейки, примыкающие к этому узлу. Он изображен на рис.1. Для упрощения описания расчетных формул входящим в него узлам присвоены более простые номера, а четырем ячейкам – номера  . Тогда уравнения (3.2) можно записать так:
. Тогда уравнения (3.2) можно записать так:
(3.3)  ,
,  .
.
В свою очередь, каждую из ячеек L, вершины которой имеют номера (1,2L,2L+1,2L+2), разделим на две пары треугольников, проведя ее диагонали (1,2L+1) и (2L,2L+2). Образующимся треугольникам присвоим номера 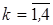 , как на рис. 2, относя их к соответствующим вершинам ячейки. Вершинам треугольника с номером k присвоим свои номера k-1, k, k+1 (см. рис.3а). Доопределение недостающих номеров очевидно и останавливаться на нем не будем. Полагаем далее:
, как на рис. 2, относя их к соответствующим вершинам ячейки. Вершинам треугольника с номером k присвоим свои номера k-1, k, k+1 (см. рис.3а). Доопределение недостающих номеров очевидно и останавливаться на нем не будем. Полагаем далее:
(3.4)  ,
, 
(3.5) 
Здесь и в дальнейшем индекс (k,L) означает, что соответствующая величина определяется в треугольнике с номером k ячейки с номером L.
Отметим весьма важное обстоятельство. Описываемая конструкция интегральной суммы (3.1) предполагает, что
(3.6)  для всех k,L.
для всех k,L.
Как будет следовать из дальнейшего, величины  представляют удвоенные площади соответствующих треугольников, и тогда требование (3.6) предполагает выпуклость всех ячеек сетки. Практика расчетов требует ослабления этого требования, и этот вопрос будет обсуждаться в §5. Пока же будем предполагать условия (3.6) выполненными.
представляют удвоенные площади соответствующих треугольников, и тогда требование (3.6) предполагает выпуклость всех ячеек сетки. Практика расчетов требует ослабления этого требования, и этот вопрос будет обсуждаться в §5. Пока же будем предполагать условия (3.6) выполненными.
Для вычисления метрических параметров в треугольнике с номером k применяются формулы, которые после введения обозначений:
(3.7)  ,
, 
 ,
, 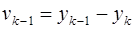
имеют вид:
(3.8) 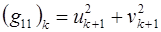 ,
, 
 ,
, 
Для них тождественно выполнен разностный аналог формулы (1.4):
(3.9) 
Кроме того, имеют место равенства:
(3.10)  ,
,  ,
,
где  - угол, образованный отрезками сетки в вершине с номером k ячейки L (см. рис.3б).
- угол, образованный отрезками сетки в вершине с номером k ячейки L (см. рис.3б).
Величины  определяются такими же формулами с использованием координат узлов сетки на предыдущем шаге по времени, а затем подвергаются корректировке, например, по формулам (2.16).
определяются такими же формулами с использованием координат узлов сетки на предыдущем шаге по времени, а затем подвергаются корректировке, например, по формулам (2.16).
Для функционала (1.8)-(1.9) без якобиана разностные уравнения (3.3) в узле 1 шаблона могут быть записаны в виде:
(3.11) 
 ,
,
где коэффициенты  вычисляются по следующим формулам:
вычисляются по следующим формулам:
(3.12) 

(3.13) 
Обратим внимание, что в этих формулах отсутствуют величины с индексом (3,L), отвечающие треугольнику с номером k=3. Это не случайно, поскольку «вклад» этого треугольника в сумму (3.1) не будет изменяться при вариации узла  . Поэтому расчет треугольника с номером k=3 можно не производить.
. Поэтому расчет треугольника с номером k=3 можно не производить.
Отметим далее, что в случае 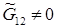 присутствие в формулах (3.12)-(3.13) отрицательных коэффициентов является обычным явлением. Следовательно, для получаемой системы линейных уравнений принцип максимума не выполняется. Это еще одна из причин тщательного подхода к конструированию системы разностных уравнений на основе положительно определенной квадратичной формы в случае работы с функционалом без якобиана.
присутствие в формулах (3.12)-(3.13) отрицательных коэффициентов является обычным явлением. Следовательно, для получаемой системы линейных уравнений принцип максимума не выполняется. Это еще одна из причин тщательного подхода к конструированию системы разностных уравнений на основе положительно определенной квадратичной формы в случае работы с функционалом без якобиана.
При получении коэффициентов  для нормировки используются величины
для нормировки используются величины 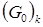 . В силу формулы (3.10) они прямо зависят от значений величин
. В силу формулы (3.10) они прямо зависят от значений величин  для углов, образуемых отрезками сетки предыдущего шага по времени во всех ее узлах. Следовательно, конструируемая система уравнений «реагирует» на малые значения любого из этих углов или на их приближение к значению
для углов, образуемых отрезками сетки предыдущего шага по времени во всех ее узлах. Следовательно, конструируемая система уравнений «реагирует» на малые значения любого из этих углов или на их приближение к значению  , т.е. должна препятствовать вырождению соответствующих ячеек. Это существенный аргумент в пользу усложнения алгоритма, связанного с разрезанием ячейки на треугольники. Если этого не делать, в формулах (3.12)-(3.13) будут участвовать лишь некоторые «усредненные» значения
, т.е. должна препятствовать вырождению соответствующих ячеек. Это существенный аргумент в пользу усложнения алгоритма, связанного с разрезанием ячейки на треугольники. Если этого не делать, в формулах (3.12)-(3.13) будут участвовать лишь некоторые «усредненные» значения  и площадь всей ячейки сетки, «смазывая» эффект ее вырождения.
и площадь всей ячейки сетки, «смазывая» эффект ее вырождения.
Заслуживает специально быть отмеченным случай 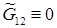 . Тогда
. Тогда  , и система (3.11) превращается в более простую:
, и система (3.11) превращается в более простую:
(3.14)  ,
, 
Более того, из (3.11) будем иметь
(3.15)  .
.
Следовательно, такая система будет удовлетворять принципу максимума.
При этом в формулах (1.6)  ,
,  .
.
Следовательно, разрезание ячеек на треугольники становится ненужным.
Поэтому так привлекательны для построения сеток в областях с фиксированными границами алгоритмы конструирования «квазиортогональных» сеток. К сожалению, в случае нестационарной задачи назначение  противоречит изложенной в § 2 идеологии, допускающей только вариации коэффициентов
противоречит изложенной в § 2 идеологии, допускающей только вариации коэффициентов  . Поэтому оно обсуждаться не будет, хотя и не закрывает возможности использования таких алгоритмов для расчета стационарных сеток.
. Поэтому оно обсуждаться не будет, хотя и не закрывает возможности использования таких алгоритмов для расчета стационарных сеток.
Обратимся теперь к функционалу (1.1)-(1.2) с якобианом в знаменателе. Соответствующая ему система сеточных уравнений (3.3) будет нелинейной из-за наличия знаменателя в формуле (3.4) и имеет существенно более громоздкий вид. Она описана в работе [4] вместе с итерационным процессом. Соответствующие расчетные формулы будут представлены в следующем параграфе.
§ 4. Итерационные процессы.
Начнем с обсуждения метода решения системы разностных уравнений (3.11) для функционала без якобиана. Заметим, что имеется хорошее начальное приближение 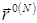 для искомого решения, определяемое формулой (2.3), и, в силу (2.4) и (2.8), отличающееся от искомого решения на величины
для искомого решения, определяемое формулой (2.3), и, в силу (2.4) и (2.8), отличающееся от искомого решения на величины  . Это обстоятельство и сама структура уравнений (3.11) вызывают естественное желание воспользоваться простейшим итерационным процессом:
. Это обстоятельство и сама структура уравнений (3.11) вызывают естественное желание воспользоваться простейшим итерационным процессом:
(4.1) 
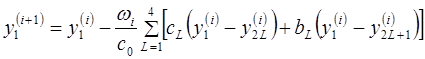
В этих формулах коэффициенты  на итерациях не меняются.
на итерациях не меняются.
(4.2) 
Управляющий параметр 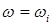 может меняться от итерации к итерации. Вопрос о его назначении будет рассмотрен ниже. Для обеспечения численной устойчивости итерационного процесса 0<w0<1.
может меняться от итерации к итерации. Вопрос о его назначении будет рассмотрен ниже. Для обеспечения численной устойчивости итерационного процесса 0<w0<1.
Для функционала (1.1)-(1.2) с якобианом, в соответствии с изложенным в конце § 3, расчетные формулы итерационного процесса имеют вид:
(4.3) 

В этих формулах  представляют соответствующие первые и вторые производные разностного функционала
представляют соответствующие первые и вторые производные разностного функционала  для центральной точки
для центральной точки  шаблона, описанного ранее в § 3, вычисленного на сетке, полученной на предыдущей итерации. Он использует так же значения матрицы коэффициентов
шаблона, описанного ранее в § 3, вычисленного на сетке, полученной на предыдущей итерации. Он использует так же значения матрицы коэффициентов  , вычисленные с помощью сетки предыдущего шага по времени и с учетом корректировки (2.16), которые остаются неизменными на всех итерациях. Каждая из величин
, вычисленные с помощью сетки предыдущего шага по времени и с учетом корректировки (2.16), которые остаются неизменными на всех итерациях. Каждая из величин  представляет сумму 12 слагаемых, отвечающих в каждой из четырех ячеек с номерами
представляет сумму 12 слагаемых, отвечающих в каждой из четырех ячеек с номерами  трем треугольникам с номерами k=1,2,4. Получение расчетных формул для этих величин представляет кропотливое, но несложное упражнение по дифференцированию, и мы их приводить не будем. Тем более, что эти формулы будут различными для треугольников k=1,2,4 из-за различной роли в них узла (x1,y1).
трем треугольникам с номерами k=1,2,4. Получение расчетных формул для этих величин представляет кропотливое, но несложное упражнение по дифференцированию, и мы их приводить не будем. Тем более, что эти формулы будут различными для треугольников k=1,2,4 из-за различной роли в них узла (x1,y1).
С точки зрения практической организации вычислений возможны два варианта. Первый состоит в том, что отбираются все величины, входящие в шаблон отдельного внутреннего узла сетки, и вычисления проводятся полностью до получения результата (x1,y1)(i+1). Второй вариант предусматривает специальный массив для накапливания величин  посредством последовательной обработки всех ячеек сетки, как это описывалось в работах [11] и [4]. С точки зрения объема вычислительной работы второй вариант предпочтительнее. Однако с точки зрения многопроцессорных вычислительных систем это далеко не очевидно и требует проверки в численном эксперименте.
посредством последовательной обработки всех ячеек сетки, как это описывалось в работах [11] и [4]. С точки зрения объема вычислительной работы второй вариант предпочтительнее. Однако с точки зрения многопроцессорных вычислительных систем это далеко не очевидно и требует проверки в численном эксперименте.
В § 3 было избрано изложение, опирающееся на первый из указанных вариантов, прежде всего, для того, чтобы представить суть алгоритма и получить структуру коэффициентов (3.12)-(3.13) в уравнениях (3.11).
Как отмечалось в работах [11], [4] и других, итерационный процесс (4.3) представляет вариант метода Ньютона-Рафсона, отличающийся от стандартного тем, что в расчете участвует только блочная диагональ матрицы вторых производных. Благодаря этому удается обойтись явными итерациями, избежав решения сложной нелинейной системы уравнений. Такой процесс применялся для расчета гармонических сеток.
Заслуживает быть отмеченным следующее обстоятельство. Поскольку для функционала (1.8)-(1.9) без якобиана будем иметь:
(4.9) 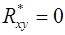 ,
, 
формулы (4.3) принимают вид:
(4.10)  ,
, 
Легко убедиться, что с учетом (4.9) формулы (4.10) тождественны формулам (4.1), поскольку  .
.
Следовательно, итерационный процесс (4.1)тоже представляет аналогичный вариант метода Ньютона-Рафсона применительно к функционалу без якобиана, представляющему в дискретной форме положительно определенную квадратичную форму от координат узлов искомой сетки. Попутно отметим, что сумма с0 коэффициентов в формуле (4.2) положительна, поскольку в соответствии с (4.9) каждый из 12 треугольников дает положительный «вклад» в нее. В самом деле, 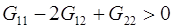 , поскольку
, поскольку  .
.
Теперь обратимся к вопросу о назначении управляющего параметра  . Специфика рассматриваемой задачи состоит в том, что главной заботой в ходе итерационного процесса является обеспечение невырожденности сетки, т.е. недопущение образования самопересекающихся ячеек. Для функционала с якобианом в знаменателе это требование еще строже: необходимо обеспечивать сохранение выпуклости всех ячеек сетки. Как уже отмечалось в § 3, пока предполагается, что требование (3.6) для исходной сетки выполнено.
. Специфика рассматриваемой задачи состоит в том, что главной заботой в ходе итерационного процесса является обеспечение невырожденности сетки, т.е. недопущение образования самопересекающихся ячеек. Для функционала с якобианом в знаменателе это требование еще строже: необходимо обеспечивать сохранение выпуклости всех ячеек сетки. Как уже отмечалось в § 3, пока предполагается, что требование (3.6) для исходной сетки выполнено.
Поэтому после каждой итерации сетка  подвергается контролю: проверке на выпуклость ячеек. Для каждой ячейки по координатам ее вершин вычисляются 4 величины
подвергается контролю: проверке на выпуклость ячеек. Для каждой ячейки по координатам ее вершин вычисляются 4 величины  , используя формулы (3.7)-(3.8). Если
, используя формулы (3.7)-(3.8). Если  для всех
для всех 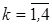 , ячейка выпукла.
, ячейка выпукла.
Нарушение этого условия хотя бы в одной ячейке влечет за собой пересчет всей сетки с уменьшенным значением параметра  . Если уменьшить
. Если уменьшить  вдвое, то нужный результат получается, если взять полусумму сеток:
вдвое, то нужный результат получается, если взять полусумму сеток:
(4.10)  ,
, 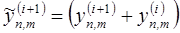 .
.
Полученная сетка  подвергается повторной проверке, и в случае необходимости процедура уменьшения
подвергается повторной проверке, и в случае необходимости процедура уменьшения  и пересчет сетки повторяется. (Во избежании «зацикливания» этого процесса в программах предусматривается ограничение числа таких «урезаний»).
и пересчет сетки повторяется. (Во избежании «зацикливания» этого процесса в программах предусматривается ограничение числа таких «урезаний»).
Жесткая процедура пересчета всей сетки в случае появления хотя бы одной «плохой» ячейки имеет практической целью сохранение гладкости сетки. Исправление ситуации посредством «лечения» отдельных «плохих» ячеек, как показывает практика, может приводить к неблагоприятным последствиям.
При расчете следующей итерации целесообразно начинать со значения параметра  , на котором закончилась предыдущая итерация, или этого значения, умноженного на коэффициент больший 1.
, на котором закончилась предыдущая итерация, или этого значения, умноженного на коэффициент больший 1.
Последняя мера диктуется соображением «не задерживать процесс», который по здравому смыслу должен улучшаться по мере сходимости итераций с уменьшением невязки решаемых уравнений.
Вопрос об исходном значении параметра  для первой итерации сложнее, поскольку (опять же по здравому смыслу) оно может зависеть от формы расчетной области на рассматриваемый момент времени. Одним из возможных решений является использование значения, на котором закончился расчет сетки в этой области на предыдущем шаге по времени, или этого значения, умноженного на коэффициент несколько больший 1 (тогда эти значения нужно сохранять в числе «областных» управляющих параметров). Тогда вопрос сводится к заданию этого пара-метра только на исходном шаге расчета, что не так уж и существенно.
для первой итерации сложнее, поскольку (опять же по здравому смыслу) оно может зависеть от формы расчетной области на рассматриваемый момент времени. Одним из возможных решений является использование значения, на котором закончился расчет сетки в этой области на предыдущем шаге по времени, или этого значения, умноженного на коэффициент несколько больший 1 (тогда эти значения нужно сохранять в числе «областных» управляющих параметров). Тогда вопрос сводится к заданию этого пара-метра только на исходном шаге расчета, что не так уж и существенно.
Теперь обратимся к вопросу о скорости сходимости описанных итерационных процессов. Несмотря на обнадеживающие слова о том, что эти процессы представляют модифицированные варианты метода Ньютона-Рафсона, практически скорость их сходимости крайне медленная. Положение спасают следующие два обстоятельства. Во-первых, на каждом очередном шаге система уравнений конструируется так, что при значениях корректирующих параметров, равных нулю, сетка предыдущего шага ей удовлетворяет точно, с нулевой невязкой (в дискретном варианте). Поэтому в соответствии с (2.4) и (2.8) итерациями предстоит погасить невязку 0(t). Этим предлагаемые алгоритмы расчета сеток принципиально отличаются от других, тянущих за собой шлейф «недоитерированности» уравнений, которые практически до сходимости довести не удается. Во-вторых, задача итерационного процесса, наряду с погашением невязки 0( t ), состоит в том, чтобы обеспечить гладкость сетки, привязанной к слегка изменившим свое положение новым границам, и в том, чтобы направить изменение сетки в приемлемое (хотелось бы, нужное) русло, не допуская ухудшения ее качества, необходимого для решения на этой сетке основной задачи. Это должно достигаться подключением соответствующих корректирующих функционалов. Если упомянутые две цели достигаются, то вопрос о том, будет ли полностью погашена упомянутая невязка 0( t ), не так уж и важен. Следующий шаг начнется с «белого листа» – конструирования новой системы разностных уравнений. Поэтому можно рассчитывать, что необходимое число итераций (пусть и очень медленно сходящихся), как правило, не придется назначать большим. Естественно, здесь существенную роль играет форма конкретной области. Кроме того, очевидно, что существенную роль играет и величина управляющих параметров p( t ) , с которыми подключаются корректирующие функционалы.
Существует ли альтернатива, позволяющая улучшить ситуацию со сходимостью итераций? В монографии [12], стр. 263, читаем:
«В общей теории итерационных методов рассматриваются методы двух типов: использующие априорную информацию об операторах итерационные схемы и не использующие (методы вариационного типа). В методах первого типа качество начального приближения не используется. В методах вариационного типа итерационные параметры выбираются из условия минимума некоторых функционалов, связанных с исходным уравнением. В этом случае итерационные параметры обладают свойством учитывать качество начального приближения».
Таким образом, рекомендации явно склоняются в пользу вариационных методов. С точки зрения создания автоматизированных систем расчета сеток такой подход может показаться перспективным. Однако в силу специфики задачи, уже описанной выше, нельзя игнорировать и опасение, что вычисленный итерационный параметр окажется непригодным, поскольку приведет к «плохой» сетке. К тому же (с учетом дополнительной вычислительной работы) нет уверенности и в том, что использование более сложных методов обеспечит заметный выигрыш при реализации алгоритмов.
|
из
5.00
|
Обсуждение в статье: Нестационарная задача для сетки. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

