Понятия о критериях согласия

Во многих случаях закон распределения случайной величины неизвестен, но на основании опытных данных делается предположение о виде закона распределения случайной величины Х. Однако для окончательного решения вопроса о виде распределения следует проверить согласуются ли результаты наблюдения с высказанным предположением. При этом, если даже предположение о виде распределения сделано правильно, закон распределения наблюдаемой случайной величины будет отличаться от теоретического закона, т.к. число наблюдений ограничено.

Поэтому следует выяснить: является ли расхождение между статистическим и теоретическим законами распределения только следствием ограниченного числа наблюдений, или оно является чем-то более существенным.

Для решения этой задачи служит критерий согласия. Существует несколько видов критерия согласия: критерий согласия Пирсона, Колмогорова, Смирного, Фишера и т.д.

Для проверки гипотезы о законе распределения случайной величины применим критерий согласия Пирсона или c2.

1. Найдем число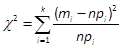

Где 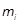- частота каждого интервала или разряда,

n – объем выборки (n = 100),

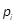- теоретическая вероятность попадания случайной величины в i интервал.

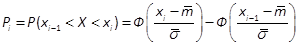
где 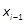, 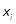- границы интервалов.

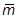 - статистическое математическое ожидание,

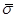 - статистическое среднеквадратическое отклонение.

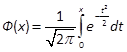- функция Лапласа.

Формула (4) следует из формулы вероятности попадания случайной величины Х, распределенной по нормальному закону, в интервал (a;b):

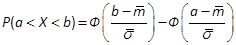
2.  Определим число степеней свободы 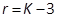, где K – число интервалов или разрядов, 3 – число связей наложенных при выборе теоретического закона распределения. Связи:

1) Условие полноты ,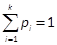

2) ,

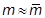3)

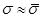
Замечание: частота mi каждого интервала должна быть не меньше 5 - 8, т.е. в этот интервал должно попадать не меньше 5 - 8 значений случайной величины. Если это не выполняется, то малочисленные интервалы следует объединить в один интервал или присоединить к соседнему, суммируя частоты.

По найденному значению c2 и числу степеней свободы r по таблице вероятностей c2 получим искомое значение вероятности Р и сравним его с выбранным условием значимости β = 0.05. Если Р< 0.05, то гипотезу о выборе теоретического закона распределения следует пересмотреть. Если Р> 0.05, то статистический и теоретический законы распределения наблюдаемой случайной величины согласуются, следовательно, нормальное распределение может быть принято в качестве аппроксимирующего закона. Вычисления сведем в таблицу 6.

Таблица

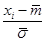
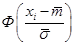
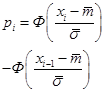
Номер интервала	Левая граница интервала	Правая граница интервала				mi	npi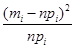
0		-8,66	-2,7006	-0,4965
1	-8,66	-4,736	-1,0092	-0,3436	0,1530	11	15,2977	1,2074
2	-4,736	-3,428	-0,4454	-0,1720	0,2702	20	27,0156	1,8218
3	-3,428	-2,12	0,1184	0,0471	0,2191	26	21,9110	0,7631
4	-2,12	-0,812	0,6822	0,2524	0,2053	18	20,5320	0,3123
5	-0,812	0,496	1,2460	0,3936	0,1412	14	14,1174	0,0010
6	0,496	4,42	2,9374	0,4983	0,1047	10	10,4726	0,0213
								4,1269

Определим число степеней свободы .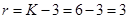

K = 6, т.к. произошло объединение трёх первых и трёх последних интервалов в один, так как частота mi каждого интервала должна быть не меньше 5 - 8.

По найденному значению c2 и числу степеней свободы r по таблице вероятностей c2 получим искомое значение вероятности Р = 0,25.

Сравним его с выбранным уравнением значимости β = 0,05: 0,25 > 0,05, Р > β.

Вывод: статистический и теоретический законы распределения наблюдаемой случайной величины согласуются, следовательно, нормальное распределение может быть принято в качестве аппроксимирующего закона.

Список литературы

1.Гмурман В.Е Теория вероятностей и математическая статистика.

2.Гмурман В.Е Руководство к решению задач по теории вероятностей и математической статистике.

3.Данко П.Е.,Попов А.Г. Высшая математика в упражнениях и задачах.

4.Пискунов Н.С. Дифференциальное и интегральное исчисления. Т 2.