 |
Главная |
Правило разыскания максимумов и минимумов
|
из
5.00
|
Пусть функция f ( x ) дифференцируема в промежутке (а, b ). Чтобы найти все ее максимумы и минимумы в этом промежутке, надо:
1) Решить уравнение f '(х) = 0 (корни этого уравнения называются критическими значениями аргумента; среди них надо будет искать значения х, дающие экстремум функции f ( x ); см. § 2).
2) Для каждого критического значения х = а исследовать, меняет ли знак производная f(x) при переходе аргумента через это значение. Если f '(х) переходит от положительных значений к отрицательным (при переходе от х < а к х > а), то имеем максимум (§ 3), если от отрицательных значений к положительным, то минимум.
Если же f ' (х) сохраняет знак, то нет ни максимума, ни минимума: при f '(х) > 0 функция f (х) в точке а возрастает, при f '(х) < 0 убывает (§ 3, замечание).
Замечание 1. Если функция f ( x ) непрерывна в промежутке (а, b),но в отдельных его точках не дифференцируема, то эти точки надо причислить к критическим и произвести аналогичное исследование.
Замечание 2. Максимумы и минимумы непрерывной функции следуют друг за другом, чередуясь.
Пример 1. Найти все максимумы и минимумы функции 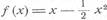
Р е ш е н и е. Данная функция всюду дифференцируема (т. е. всюду имеет конечную производную) f '(х) = 1— х.
1) Решаем уравнение 1— х = 0. Оно имеет единственный корень х = 1.
2) Производная f '(х) = 1 — х меняет знак при переходе аргумента через значение х = 1. Именно, при х < 1 производная положительна, при х > 1 —отрицательна. Значит, критическое значение х = 1 дает максимум. Других экстремумов у функции нет.
Пример 2. Найти все максимумы и минимумы функции
f ( x ) = ( x - 1)2 ( x +1). (1)
Р е ш е н и е. Данная функция всюду дифференцируема. Имеем:
f '(х) = 2(х — 1) (х + 1)3 + 3 (х — 1)2 (х + 1)2 = (х— 1)(х + 1)2(5х— 1).
1) Решаем уравнение f'(х) = 0. Его корни (расположенные в порядке возрастания) будут:
х1 = — 1, х2 = 1/5; х3 = 1. (2)
2) Представив производную в виде
f(х) = 5 (х + 1)2 (х – 1/5) (х - 1), (3)
исследуем каждое из критических значений.
а) При х < —1 все три двучлена формулы (3) отрицательны, так что слева от х = — 1 имеем:
f '(х) = 5 (-)2(-)(-) = +. (4)
Пусть аргумент перешел через значение х1= — 1, но не дошел до следующего критического значения х2 = 1/5. Тогда двучлен х + 1 стал положителен, а два других двучлена формулы (3) остаются отрицательными, и мы имеем: f '(х) = 5 (+)2 (-)(-) = +. (5)
Сравнив (4) и (5), видим, что при переходе
Рис. 11 через критическое значение х1= -1 производная не меняет знака, оставаясь положительной. Значит, в точке х =-1 экстремума нет; здесь функция f(x) возрастает (рис. 11).
б) Исследуем ближайшее большее критическое значение х2 = 1/5. В достаточной близости слева (т. е. между х1 = — 1 и х2 = 1/5) производная в силу (5) положительна. В достаточной близости справа (между х1 = 1/5 и х2 = +1) второй сомножитель положителен, и мы имеем:
f ' (х) = 5 (+)2(+) (-) = - . (6)
Сравнив (5) и (6), видим, что знак производной при переходе через х2 = 1/5 меняется с плюса на минус [функция f(х) от возрастания переходит к убыванию]. Значит, в точке x = 1/5 функция имеет максимальное значение; оно равно f (1/5) = (1/5 – 1)2 (1/5 + 1) ~ 1,1.
в) Исследуем последнее критическое значение х3 = 1. В достаточной близости слева производная в силу (6) отрицательна. Справа от х3 = 1 имеем:
f '(х) = 1/5 (+)2 (+) (+) = + . (7)
При переходе через х = 1 производная меняет знак с минуса на плюс [функция f(х) переходит от убывания к возрастанию]. Значит, при х = 1 функция имеет минимальное значение; оно равно
f (х) = (1 - 1)2(1 + 1)3 = 0.
П р и м е р 3. Найти все экстремумы функции 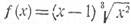
Р е ш е н и е. Данная функция дифференцируема при всех положительных и отрицательных значениях х, и мы имеем:
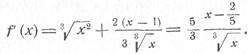
В точке же х = 0 функция f(x) не дифференцируема (ее производная бесконечна). Поэтому (см. замечание 1) имеем два критических значения: x1 = 0 и х2 = 2/5.
При х < 0 имеем: 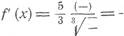
При 0 < х < 2/5 имеем: 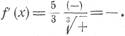
При х > 2/5 имеем: 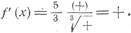
Значит, в точке х = 0 функция 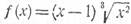 имеет максимальное значение f (0) = 0, а в точке x = 2/5 - минимальное значение
имеет максимальное значение f (0) = 0, а в точке x = 2/5 - минимальное значение
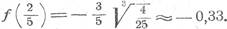
|
из
5.00
|
Обсуждение в статье: Правило разыскания максимумов и минимумов |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

