Оценивание закона распределения

Задание к курсовой работе

Разработать программу анализа параметров и характеристик реализации случайного процесса.

 

Описание исходных данных.

Исходный массив данных, представляющих собой реализацию из 2048 отсчетов многомерного случайного сигнала записан в файле «EEG1(2,3,4).txt» текстового формата. Количество колонок массива соответствует числу компонент случайного процесса (16), количество строк – числу отсчетов (2048). Интервал дискретизации, использованный при регистрации сигнала, равен 10 мс.

 

Задача 1. Оценка статистических характеристик реализации

Случайного процесса.

Выполнить оценку математического ожидания и дисперсии заданных в соответствии с номером варианта компонент реализации СП. Оценить их вариативность (дисперсию), выполнив расчеты для разных временных интервалов. Сделать выводы.

 

Задача 2. Оценка плотности распределения реализации

Случайного процесса.

Выбрать количество интервалов, рассчитать и построить гистограмму распределения для заданных компонент реализации СП.

 

Задача 3. Оценка корреляционных характеристик реализации

Случайного процесса.

Оценить и построить корреляционные функции заданных в соответствии с номером варианта компонент СП.

Оценить и построить взаимные корреляционные функции компонент СП.

Задача 4. Оценка спектральных характеристик реализации

Случайного процесса.

Исследовать спектральные характеристики (СПМ) случайного процесса методом Уэлча.

Длительности интервалов (сегментов сигнала) выбрать из таблицы.

Для снижения несостоятельности оценки использовать выделяющие функции или сглаживание спектральными окнами, выбранными в соответствии с вариантом.

Сравнить оценки СПМ, выполненные без использования и с использованием выделяющих функций, а также в зависимости от размера выделяющей функции.

 

Вариант №	Номера каналов	Спектр. окно	Длител. интервала
7	3,4,5	Чебышева	128

Основные теоретические сведения

 

В любой радиоэлектронной системе приходится иметь дело с обработкой случайных сигналов. Такая обработка проводится с различными целями. Часто задачей этой обработки является оценка различных характеристик, начиная от оценки моментов и заканчивая оценкой корреляционной функции, закона распределения и спектра мощности.

 

Оценка моментов

Оценка математического ожидания:

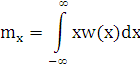
где w(x) –плотность распределения случайной величины.

Для стационарного эргодического процесса:

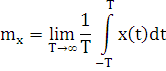
для дискретного сигнала:

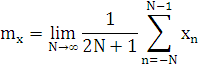
В качестве оценки математического ожидания используют:

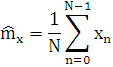
Качество оценки определяется степенью её разброса вокруг точного значения. Количественно оценка описывается доверительным интервалом значений вокруг точной величины, в который оценка попадает с заданной вероятностью. Под доверительной вероятностью понимается площадь под кривой внутри границ доверительного интервала. Чем уже интервал, тем лучше оценка. Количественной мерой ширины интервала служит дисперсия оценки:

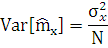
Оценка называется состоятельной, если с увеличением объема выборки дисперсия оценки стремится к нулю. Оценки могут выполняться по разным правилам и формулам.

Часто используется оценка максимального правдоподобия. Такая оценка основана на рассмотрении совместной плотности вероятности, как функции оцениваемого параметра.

Оценкой максимального правдоподобия называют:

 

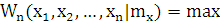
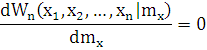
- уравнение правдоподобия. Его решение: .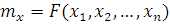

Пусть 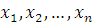 - независимые случайные величины, тогда

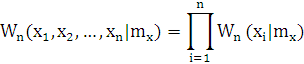
Функция правдоподобия:

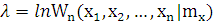
Для нормального закона распределения: .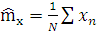

 

Оценкой дисперсии для нормального случайного процесса является:

 

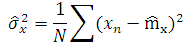
Оценивание закона распределения

 

Существует два класса законов распределения:

· Интегральный

· Дифференциальный

Для оценки сигнала используется дифференциальный закон (плотность распределения).

Известно два способа оценки:

· Непараметрический (когда тип исходного распределения неизвестен)

à Гистограммный

à Парзена

à Разложения на базисные функции

à Полигонов Смирнова

à К-ближайших соседей

· Параметрический (известен закон, надо определить параметры)

Мы имеем дело с априорно непрерывной плотностью распределения вероятности, отличной от нуля на всем рассматриваемом интервале х. Объем выборки должен быть велик.

Наиболее простой и часто используемый метод – метод гистограмм.

Область возможных значений сигнала разбивается на непересекающиеся подобласти, в одномерном случае это интервалы 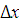, в многомерном – параллелепипеды. Затем выборка исходных значений сигнала перебирается и подсчитывается число значений выборки попавших в к-ю подобласть. Затем оценивается закон распределения:

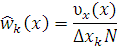
Размеры интервалов 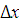 делаются одинаковыми. Для выбора количества интервалов и их ширины нет общих правил.

Достоинства такой гистограммы:

+ Простота оценивания

+ Ясный физический смысл

Недостатки:

- При увеличении объема выборок, но неизменном количестве интервалов, оценка не сходится к точному значению закона распределения.

Сходимостью этой оценки к точному значению можно обеспечить, если выполняются дополнительные условия. При увеличении N необходимо увеличение числа интервалов и уменьшения их величины. При этом необходимо выполнить следующие условия:

1.

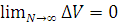
2.

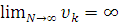
3.

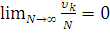
Первое условие обеспечивает сходимость пространственно усредненной величины к точному значению оценки, при этом подобласти должны сокращаться с одинаковой скоростью, а закон распределения должен быть непрерывным.

Второе условие: закон распределения на всем интервале отличен от нуля.

Третье условие обеспечивает сходимость оценки к точному закону распределения.

Существует два способа выполнения этих условий:

1. Сжатие подобласти таким образом, чтобы 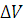 был обратно пропорционален корню квадратному из N (метод Парзена).

2. Подобласти так сжимаются, чтобы 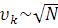 (метод к-ближайших соседей)

В случае обработки цифрового сигнала общий объем является целой степенью 2. Максимальное значение сигнала 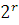, где r-число разрядов используемого кода. Поэтому границы интервалов выбираются так, чтобы они совпадали с уровнями квантования, их количество 8-20.

 

Корреляционный анализ

 

Корреляционный анализ наряду со спектральным играет большую роль в теории сигналов. Говоря кратко, его смысл состоит в количественном измерении степе­ни сходства различных сигналов. Для этого служат корреляционные функции.