Весовые функции (окна)

Для уменьшения растекания спектра при ДПФ применяются весовые функции (weighting functions), которые также называют окнами (windows). В этом случае перед расчетом ДПФ сигнал умножается на весовую функцию w(k),которая должна спадать к краям сегмента. Формула прямого ДПФ при использова­нии весовых функций принимает следующий вид:

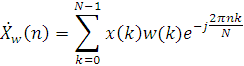
Роль весовой функции в этой формуле можно рассматривать с различных точек зрения. Сначала проанализируем ситуацию во временной области. Если мы ис­пользуем весовую функцию, которая имеет максимум в середине (при k = N/2)и плавно спадает к краям (k = 0 и k = N-1), то это приведет к ослаблению эффектов, связанных с возникновением скачков сигнала при периодическом повторе­нии анализируемой конечной последовательности, и, таким образом, к уменьше­нию растекания спектра.

Аналогичный вывод можно сделать, рассмотрев влияние весовой функции в час­тотной области. Умножение сигнала на весовую функцию соответствует свертке спектров сигнала и весовой функции. Это приводит к тому, что пики, содержащиеся в спектре сиг­нала, несколько расширяются. Однако при этом становится возможно умень­шить уровень боковых лепестков спектральной функции, что и является целью применения весовых функций.

Если трактовать ДПФ как фильтрацию, при использовании весовой функции w(k)получаются частотные характеристики фильтров следующего вида:

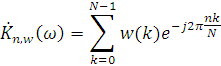
Выбирая весовую функцию w(k) определенным образом, можно уменьшить уро­вень боковых лепестков частотой характеристики фильтров, соответствующих отдельным каналам ДПФ. Естественно, платой за это является расширение цен­трального лепестка частотной характеристики.

Текст программы.

 

-----------------------------------

Kurs . m

-----------------------------------

load EEG1.txt                      %загрузка исходного файла

k=input('Введите номер канала k='); %выбор каналов     

l=input('Введите номер канала l=');

m=input('Введите номер канала m=');

x(:,1)=EEG1(:,k);                    %запись выбранных каналов

x(:,2)=EEG1(:,l);                  %в отдельную матрицу

x(:,3)=EEG1(:,m);

clc;

st                                 %переход в меню

 

-----------------------------------

St . m

-----------------------------------

%меню выбора задания

function st

disp('Выберите задание')

disp('<a href="matlab:z1(x)">Задание 1. Оценка статистических характеристик реализации случайного процесса</a>')

disp('<a href="matlab:z2(x)">Задание 2. Оценка плотности распределения реализации случайного процесса</a>')

disp('<a href="matlab:z3(x)">Задание 3. Оценка корреляционных характеристик реализации случайного процесса</a>')

disp('<a href="matlab:z4(x)">Задание 4. Оценка спектральных характеристик реализации случайного процесса</a>')

 

-----------------------------------

Z 1. m

-----------------------------------

%Функция расчета математического ожидания и дисперсии

%для выбранных компонент реализации СП

function z1(x)

format short g

%Следующий цикл формирует 4 массива:

%mx - c мат.ожиданием

%varx - c дисперсией

%sostmx – вариативность мат. ожидания

%sostvarx – вариативность дисперсии

%1 столбец массива - временные интервалы

%2,3,4 столбцы соответствуют разным каналам

for ii=1:3

dlit=64;

for jj=1:4

    for kk=1:4

        a=(kk-1)*dlit+1;

        b=kk*dlit;

        tmpmx(kk)=mean(x(a:b,ii))

        tmpvarx(kk)=var(x(a:b,ii))

    end;

    mx(jj,1)=dlit;

    mx(jj,ii+1)=mean(tmpmx);

    varx(jj,1)=dlit;

    varx(jj,ii+1)=mean(tmpvarx);

    sostmx(jj,1)=dlit;

    sostmx(jj,ii+1)=var(tmpmx);

    sostvarx(jj,1)=dlit;

    sostvarx(jj,ii+1)=var(tmpvarx);

    dlit=dlit*2;

end;

 end

%Вывод данных

disp('-----------------------------------------------------');

disp('           |         N канала         ');

disp(' Длит. ------------------------------------')

disp(' интервала | 1 | 2 | 3 ');

disp('-----------------------------------------------------');

disp('Математическое ожидание');

disp(mx);

disp('Дисперсия');

disp(varx);

disp('Дисперсия оценки математического ожидания');

disp(sostmx);

disp('Дисперсия оценки дисперсии');

disp(sostvarx);

grafik=input('Хотите построить графики дисперсии оценок? (1 - Да, 2 - Нет) ');

if grafik == 1

figure;

subplot(2,1,1);

plot(sostmx(:,2:4));

title('Графики дисперсии оценки математического ожидания для разных временных интервалов','FontName','Times New Roman');

k=legend('Канал 1','Канал 2','Канал 3');

set(k,'FontName','Times New Roman');

subplot(2,1,2);

plot(sostvarx(:,2:4));

title('Графики дисперсии оценки дисперсии для разных временных интервалов','FontName','Times New Roman');

k=legend('Канал 1','Канал 2','Канал 3');

set(k,'FontName','Times New Roman');

end;

st

-----------------------------------

Z 2. m

-----------------------------------

%Функция построения гистограмм для заданных компонент

function z2(x)

disp('Введите количество интервалов (не менее 5)');

disp('0 - автоматический выбор');

nbins=input('Количество интервалов = ');

figure;

for ii=1:3

subplot(3,1,ii);

if nbins<5

   hist(x(:,ii));

else

   hist(x(:,ii),nbins);

end;

title(['Гистограмма',num2str(ii),'-го канала'],'FontName','Times New Roman');

end

st

-----------------------------------

Z 3. m

-----------------------------------

%Функция оценки корреляционных характеристик

function z3(x)

N=50;                          %размер корреляционной матрицы

[temp1, R1]=corrmtx(x(:,1) ,N); %Расчет АКФ (корреляционных

[temp2, R2]=corrmtx(x(:,2) ,N); %матриц)

[temp3, R3]=corrmtx(x(:,3) ,N);

k=0:N;

subplot(3,1,1);

stem(k, R1(1,:));

title('АКФ 1-го канала','FontName','Times New Roman');

subplot(3,1,2);

stem(k, R2(1,:));

title('АКФ 2-го канала','FontName','Times New Roman');

subplot(3,1,3);

stem(k, R3(1,:));

title('АКФ 3-го канала','FontName','Times New Roman');

R4 = xcorr(x(:,1),x(:,2));     %Расчет ВКФ

R5 = xcorr(x(:,1),x(:,3));

R6 = xcorr(x(:,2),x(:,3));

figure;

subplot(3,1,1);

stem(R4(2048:2098));

title('ВКФ 1-го и 2-го каналов','FontName','Times New Roman');

subplot(3,1,2);

stem(R5(2048:2098));

title('ВКФ 1-го и 3-го каналов','FontName','Times New Roman');

subplot(3,1,3);

stem(R6(2048:2098));

title('ВКФ 2-го и 3-го каналов','FontName','Times New Roman');

st

-----------------------------------

Z 4. m

-----------------------------------

%Функция расчета СПМ методом Уэлча

function z4(x)

nxt=1;

ur=input('Введите уровень боковых лепестков =');

dlit=input('Введите длительность сигнала =');

while nxt>0

long=input('Введите длину окна n=');

w=chebwin(long,ur);                            %окно Чебышева

figure;

 plot(w);

figure;

for ii=1:3

   subplot(3,2,(2*ii-1))

   pwelch(x(1:dlit,ii),boxcar(dlit),[],[],100); %СПМ без выделяющей функции

   title(['СПМ ',num2str(ii),' канала без выделяющей функции'],'FontName','Times New Roman');

  subplot(3,2,2*ii)

   pwelch(x(1:dlit,ii),w,[],[],100);          %Сглажено с помощью окна Чебышева

   title(['СПМ ',num2str(ii),' канала с использованием окна Чебышева'],'FontName','Times New Roman');

end;

nxt=input('Изменить длину окна и продолжить расчет? (1-Да, 0-Нет) ');

end;

st