Корреляционная функция

Корреляционная функция (КФ; английский термин — correlation function, CF) детерминированного сигнала с конечной энергией представляет собой интеграл (в бесконечных пределах) от произведения двух копий сигнала, сдвинутых друг относительно друга на время τ:

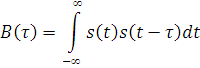
Корреляционная функция показывает степень сходства между сигналом и его сдвинутой копией — чем больше значение корреляционной функции, тем это сходство сильнее. Кроме того, корреляционная функция обладает следующими свойствами:

1. Значение КФ при 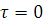 равно энергии сигнала, то есть интегралу от его квад­рата:

2. КФ является четной функцией своего аргумента τ: .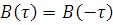

3. Значение КФ при τ = 0 является максимально возможным значением:

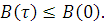
4.  C ростом абсолютного значения τ КФ сигнала с конечной энергией затухает:

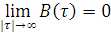
5. Если сигнал s(t) не содержит особенностей в виде дельта-функций, его КФ не может иметь разрывов (то есть обязана быть непрерывной функцией).

6. Если сигнал — напряжение, то размерность его КФ равна В² • с.

Взаимная корреляционная функция

Если КФ показывает степень сходства между сдвинутыми копиями одного и того же сигнала, то взаимная корреляционная функция (ВКФ; английский тер­мин — cross-correlation function, CCF) позволяет измерить аналогичную величи­ну для сдвинутых экземпляров двух разных сигналов.

Общий вид формулы КФ сохраняется, но под интегралом стоит произведение двух разных сигналов, один из которых задержан на время τ.

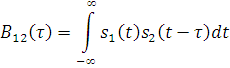
Свойства ВКФ несколько отличаются от свойств КФ:

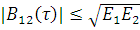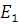1. , где и 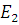 — энергии сигналов s₁(t) и s₂(t).

2. 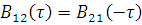, то есть изменение знака τ равносильно взаимной перестанов­ке сигналов.

3. Значение ВКФ приτ = 0 ничем не выделяется; максимум может быть распо­ложен в любом месте оси .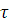

4. С ростом абсолютного значения т ВКФ сигналов с конечной энергией зату­хает: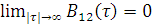

5. Если сигналы s₁(t) и s₂(t) не содержат особенностей в виде дельта-функций, их ВКФ не может иметь разрывов (то есть обязана быть непрерывной функцией).

6. Если сигналы — напряжение, то размерность их ВКФ равна В² • с.

Для периодических сигналов понятие ВКФ обычно не применяется, хотя оно мо­жет быть введено в случае, если сигналы s₁(t) и s₂(t) имеют одинаковый период.

Связь между корреляционными функциями и спектрами

Сигналов

Поскольку как корреляционные функции, так и спектры являются интегральны­ми преобразованиями анализируемых сигналов, логично предположить, что эти характеристики как-то связаны друг с другом. Для выявления этой связи подвергнем взаимную корреляционную функцию преобразованию Фурье, считая, что сигналы s₁(t) и s₂(t) имеют спектральные функци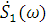и  и  :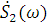

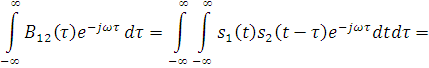
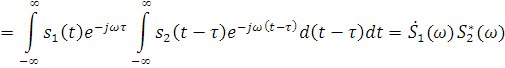
Полученный результат очень прост: ВКФ связана преобразованием Фурье с так называемым взаимным спектром сигналов. Взаимный спектр 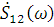 для сигналов s₁(t) и s₂(t) представляет собой произведение их спектральных функций, одна из которых подвергнута комплексному сопряжению:

.

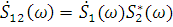Отсюда можно сделать очень важный вывод: если спектры сигналов не перекры­ваются, то их взаимный спектр равен нулю на всех частотах, а значит, равна нулю и их ВКФ при любых временных сдвигах τ. Таким образом, сигналы с непе­рекрывающимися спектрами являются некоррелированными.

Приняв s₁(t) = s₂(t) = s(t), получаем аналогичный результат для КФ:

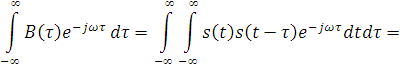
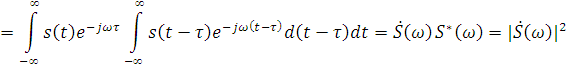
Итак, КФ сигнала связана преобразованием Фурье с квадратом модуля спектраль­ной функции, или с энергетическим спектром сигнала.

Отсюда следует еще один важный факт: КФ сигнала не зависит от его фазового спектра. Следовательно, сигналы, амплитудные спектры которых одинаковы, а фазовые различаются, будут иметь одинаковую КФ. Еще одно следствие за­ключается в том, что по КФ нельзя восстановить исходный сигнал (опять же из-за утраты информации о фазе).