Конечные сечения в квантовой механике

 

Обсудим подробнее вопрос о том, какие потенциалы приводят в квантовой механике к конечным сечениям. Пусть на больших расстояниях . В классической механике при рассеянии в таком поле полное сечение бесконечно, так как любым большим прицельным параметрам ρ соответствуют хотя и малые, но конечные классические углы отклонения

 

 

В квантовой механике для частицы с прицельным параметром ρ (у нее  неопределенность поперечного импульса поэтому квантовая неопределенность угла отклонения равна

 

 

Таким образом, при и поэтому квантомеханические результаты могут существенно отличаться от классических.

Зная поведение U(r) на больших расстояниях, где взаимодействие всегда слабое и поэтому борновское приближение применимо, можно оценить поведение амплитуды в области малых углов рассеяния:

 

 

Отсюда получаем, что дифференциальное сечение

 

 

конечно при θ → 0,если n>3, а полное сечение

 

 

конечно при n>2.

Опыты по рассеянию быстрых электронов на ядрах. Формфакторы элементарных частиц.

Фазовая теория рассеяния

 

Рассеяние на сферически симметричном потенциале является симметричным, то есть ψ(r) зависит лишь от r и θ,но не от ϕ. Поэтому разложение этого решения по парциальным волнам содержит лишь

 

                  (3.1)

 

Как известно (центральное поле сил),

 

 

Чтобы выполнялось граничное условие (1.2), необходимо

 

 

Тогда

 

 

Понятие о неупругом сечении

 

Решение (3.1) при r →∞ можно представить не только в виде (1.2), но и в виде двух сферических волн, расходящейся и сходящейся:

 

 

(разумеется, при таком разбиении расходящаяся волна отличается от в (1.2)). Парциальная амплитуда расходящейся волны отличается на множитель 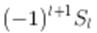от соответствующей амплитуды в сходящейся волне. Если нет поглощения частиц силовым центром, то этот множитель должен быть по модулю равен единице, .

Если есть поглощение, то 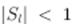, а величина характеризует уменьшение потока частиц в расходящейся волне по сравнению с потоком частиц в сходящейся. Действительно,

 

 

Поэтому неупругое сечение равно

 

 

Оптическая теорема

 

Для процессов рассеяния и поглощения существуют определенные ограничения и связи. Введем понятие парционального сечения , представив 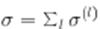. В классической механике момент импульса , поэтому , а под парциальным сечением естественно понимать площадь кольца между окружностями радиусов и ,то есть

 

 

Парциальные сечения для упругого, неупругого и полного 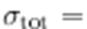 сечения можно записать в виде

 

 

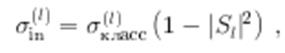
При нет ни поглощения, ни рассеяния; при есть только рассеяние, но нет поглощения. Так как , то

 

 

Если есть поглощение частиц  , то непременно происходит и рассеяние частиц. Поглощение максимально при 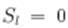и в этом случае

 

 

Еще одно соотношение возникает, если сравнить

 

 

с выражением для мнимой частицы амплитуды рассеяния на угол

нуль:

 

 

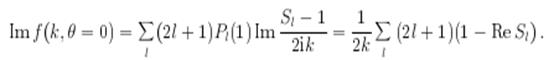
Отсюда получаем оптическую теорему:

 

 

Ее смысл тот же, что и в оптике: ослабление падающего потока происходит за счет интерференции падающей волны и волны, рассеянной под очень малыми углами.