 |
Главная |
Приложения дифференциального исчисления к геометрии
|
из
5.00
|
Аналитическое представление кривых.
1) Кривые на плоскости (в прямоугольных координатах).
Уравнение вида
у= f (х) или x = g ( y ), (1)
есть способ задания кривой, когда одна из текущих координат ее точки представляется в виде (однозначной) явной функции от другой координаты, это явное задание (или представление) кривой. Всякое другое задание может быть сведено к этому.
Также существует неявное задание кривой, т.е. о представлении кривой уравнением вида
F { x , y ) = 0, (2)
неразрешенным ни относительно х, ни относительно у.Такое уравнение носит название неявного уравнения кривой.
Если в точке (х0, у0) кривой выполнено условие
 или
или 
то, по крайней мере, в некоторой окрестности этой точки кривая может быть представлена явным уравнением (1) того или другого вида (причем фигурирующая в нем функция / или g непрерывна вместе со своей производной).
Таким образом, только точки (х0, _у0) кривой, для которых выполняются сразу оба условия
 ,
,  (3)
(3)
могут иметь ту особенность, что в их окрестности кривая не представима явным уравнением (ни того, ни другого вида). Точки кривой, удовлетворяющие уравнениям (3), и называют особыми.
Уравнения вида
 , (4)
, (4)
устанавливающие зависимость текущих координат точки от некоторого параметра t , также определяют кривую на плоскости. Уравнения называются параметрическими; они дают параметрическое представление кривой.
Кривая есть геометрическое место точек, удовлетворяющих аналитическому соотношению вида (1), (2) или (3).
2) Кривые на плоскости (в полярных координатах).
Во многих случаях оказывается проще представлять кривые их полярными уравнениями, устанавливающими зависимость между текущими полярными координатами r,  точек кривой. Зависимость между r и
точек кривой. Зависимость между r и  может быть задана в явной, неявной или параметрической форме. Вид явного уравнения:
может быть задана в явной, неявной или параметрической форме. Вид явного уравнения: 
Если перейти к прямоугольным координатам, взяв полюс за начало, а полярную ось - за ось х, то уравнения
x = r cos 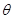 =f(
=f(  ) cos
) cos 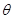 , у=rsin
, у=rsin  =f(
=f(  )sin
)sin 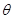
дадут параметрическое представление нашей кривой, причем роль параметра здесь будет играть полярный угол  .
.
Формулы: 
Показывают, что особая точка может встретится лишь в том случае, если 
Длина плоской кривой
Пусть имеем (незамкнутую или замкнутую) плоскую кривую АВ, заданную параметрически уравнениями:
 ,
,
где функции  и
и  здесь предполагаются непрерывными. Пусть кратных точек на кривой нет, так что каждая точка получается лишь при одном значении параметра t. При этих предположениях кривую будем называть непрерывной простой кривой.
здесь предполагаются непрерывными. Пусть кратных точек на кривой нет, так что каждая точка получается лишь при одном значении параметра t. При этих предположениях кривую будем называть непрерывной простой кривой.
Точка А отвечает значению параметра t=t0, а точка B-значению t=T. Точка А называется начальной, а точка B конечной точкой кривой. Из двух отличных от A и B та считается следующей, которая отвечает большему значению параметра.
Возьмем на кривой ряд точек: А = М0, М1 ,М2 ,..., Мi ,Mi+1,…, Мn = В так, чтобы они шли в указанном возрастающим значениям параметра t0 <t1<t2<…<ti<ti+1<…<tn.

Рис. 16
Соединяя эти точки последовательно прямолинейными отрезками (рис. 16), мы получим ломаную М0М1 ... Мn-1 Мnвписанную в кривую АВ.
Длиной кривой АВ, называется точная верхняя граница S для множества периметров р всевозможных вписанных в кривую ломаных: S=Sup{p}.
Если это число S конечно, то кривая называется спрямляемой.
Пусть функции  и
и 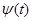 имеют непрерывные производные
имеют непрерывные производные  и
и  на
на  . Тогда длина дуги вычисляется по формуле
. Тогда длина дуги вычисляется по формуле  или
или  (1)
(1)
Если кривая задана полярным уравнением r = g ( 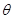 ), то это равносильно заданию ее параметрическими уравнениями
), то это равносильно заданию ее параметрическими уравнениями
х = r cos 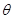 , у = rsin
, у = rsin  ,
,
где параметр - 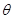 ; дуга будет функцией от
; дуга будет функцией от 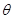 : s = s (
: s = s ( 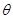 ). Так как
). Так как

То 
и формула (1) примет вид:

Кривизна плоской кривой.
Пусть дана простая кривая x =  ( t ), y =
( t ), y =  ( t ) ( t 0
( t ) ( t 0  ) , (1)
) , (1)
где функции 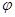 и
и  предполагаются непрерывными вместе со своими производными первого и второго порядка.
предполагаются непрерывными вместе со своими производными первого и второго порядка.

Рис. 17
Пусть  , есть дуга кривой; рассмотрим касательные МТ и M1T1 проведенные в конечных точках этой дуги. Кривизну кривой будем характеризовать углом поворота касательной, рассчитанным на единицу длины дуги, т.е. отношением
, есть дуга кривой; рассмотрим касательные МТ и M1T1 проведенные в конечных точках этой дуги. Кривизну кривой будем характеризовать углом поворота касательной, рассчитанным на единицу длины дуги, т.е. отношением  , где угол
, где угол  измеряется в радианах, а длина
измеряется в радианах, а длина  - в выбранных единицах длины. Это отношение называют средней кривизной дуги кривой.
- в выбранных единицах длины. Это отношение называют средней кривизной дуги кривой.
Кривизной кривой в точке М называется предел, к которому стремится средняя кривизна дуги MM1 ,когда точка М1 вдоль по кривой стремится к М.
Кривизну кривой в данной точке обозначаем буквой k :

Возьмем на участке кривой точку М, и пусть ей отвечает значение s дуги. Придав s произвольное приращение  , получим другую точку
, получим другую точку  (рис. 18). Приращение
(рис. 18). Приращение  угла наклона касательной при переходе от М к М1 даст угол
угла наклона касательной при переходе от М к М1 даст угол  между обеими касательными:
между обеими касательными: 

Рис. 18
Так как  , то средняя кривизна будет равна
, то средняя кривизна будет равна 
Устремив MM 1 =  к нулю, получим выражение для кривизны кривой в точке М:
к нулю, получим выражение для кривизны кривой в точке М:
 (2)
(2)
Перепишем формулу (2) иначе:
 (3)
(3)
 . Нужно найти
. Нужно найти  . Так как
. Так как
 и
и  , то
, то

Подставив в (3) значения  и
и  получим конечную формулу:
получим конечную формулу:
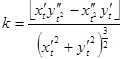 (4)
(4)
Если кривая задана явным уравнением y = f ( x ), то эта формула принимает вид:

Если дано полярное уравнение кривой: r = g(  ), то можно перейти к параметрическому представлению в прямоугольных координатах, принимая за параметр
), то можно перейти к параметрическому представлению в прямоугольных координатах, принимая за параметр 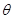 . Тогда с помощью (4) получается:
. Тогда с помощью (4) получается:

Пример.
Найти кривизну линии  в точке с абсциссой
в точке с абсциссой 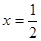
Решение
Находим 
Вычисляем значения производных при  :
:
 ;
; 
Кривизна линии 
Литература
1. Д.К. Фаддеев, Н.С. Никулин, И.Ф. Соколовский Элементы высшей математики для школьников. - М.: Наука,1987. - 336 с.
2. Н.Я. Виленкин, К.А. Бохан и др. Задачник по курсу математического анализа. - М.,”Просвещение”,1981. – 343 с.
3. Г.М. Фихтенгольц Курс дифференциального и интегрального исчисления. - М.: Наука, 1969.
4. П.Е. Данко и др. Высшая математика в упражнениях и задачах. - Издательство “Высшая школа”, 1998.
|
из
5.00
|
Обсуждение в статье: Приложения дифференциального исчисления к геометрии |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

