 |
Главная |
Максимум и минимум функций
|
из
5.00
|
Если функция f(x),определенная и непрерывная в промежутке [а, b],не является в нем монотонной, то найдутся такие части  промежутка [а, b], в которых наибольшее или наименьшее значение достигается функцией во внутренней точке.
промежутка [а, b], в которых наибольшее или наименьшее значение достигается функцией во внутренней точке.
Точка х0 называется точкой локального минимумадля функции f(x),если ее значение f(x0)в этой точке меньше всех значений в некоторой ее окрестности  , то есть
, то есть  . Значение f(x0)называется локальным минимумомфункции f ( x ). Глобальным (всеобщим) минимумомназывается значение функции, наименьшее среди значений на всем интервале.
. Значение f(x0)называется локальным минимумомфункции f ( x ). Глобальным (всеобщим) минимумомназывается значение функции, наименьшее среди значений на всем интервале.
Точка локального максимума - точка х0, для которой f(x0) - наибольшее среди всех значений в некоторой окрестности точки х0. Локальный максимум функции - значение f(x0) в точке локального максимума, глобальный максимум - наибольшее значение функции, заданной на интервале.
На рис. 5 точка х0 - точка локального минимума функции f(x), x1 есть точка локального максимума. Глобальные минимум и максимум достигаются на концах а и b промежутка задания функции.

Рис. 5
Максимум и минимум функции носят общее название экстремумов, и точки, в которых они достигаются, называются точками экстремумов.
Рассмотрим задачу, в которой нужно найти все значения аргумента, доставляющих функции экстремум.
Предположим, что для функции f(x) в промежутке (a.b) существует конечная производная. Если в точке x0 функция имеет экстремум, то применив к промежутку  теорему Ферма (пусть функция f(x) определена в некотором промежутке и во внутренней точке с этого промежутка принимает наибольшее (наименьшее) значение. Если существует двусторонняя конечная производная
теорему Ферма (пусть функция f(x) определена в некотором промежутке и во внутренней точке с этого промежутка принимает наибольшее (наименьшее) значение. Если существует двусторонняя конечная производная 
 в этой точке, то необходимо
в этой точке, то необходимо  ), получим, что
), получим, что  : в этом состоит необходимое условие экстремума. Экстремум нужно искать только в тех случаях, где производная равна 0. Эти точки называются стационарными.
: в этом состоит необходимое условие экстремума. Экстремум нужно искать только в тех случаях, где производная равна 0. Эти точки называются стационарными.
Не каждая стационарная точка доставляет функции экстремум: необходимое условие не является достаточным. Например, для функции  производная
производная  обращается в нуль при x=0, но в этой точке функция не имеет экстремума: она всё время возрастает.
обращается в нуль при x=0, но в этой точке функция не имеет экстремума: она всё время возрастает.
Если точка  - стационарная точка для функции f ( x ) или если в этой точке не существует для нее двусторонней конечной производной, то точка х0 является лишь «подозрительной» по экстремуму и подлежит проверке достаточных условий для существования экстремума.
- стационарная точка для функции f ( x ) или если в этой точке не существует для нее двусторонней конечной производной, то точка х0 является лишь «подозрительной» по экстремуму и подлежит проверке достаточных условий для существования экстремума.
Первое правило для испытания “подозрительного” значения х0: подставляя в производную  сначала х<х0, а затем x>x0, устанавливаем знак производной вблизи от точки х0 слева и справа от нее; если при этом производная
сначала х<х0, а затем x>x0, устанавливаем знак производной вблизи от точки х0 слева и справа от нее; если при этом производная  меняет знак плюс на минус, то имеем максимум, если меняет знак минус на плюс, то - минимум; если же знака не меняет, то экстремума нет.
меняет знак плюс на минус, то имеем максимум, если меняет знак минус на плюс, то - минимум; если же знака не меняет, то экстремума нет.
Это правило решает вопрос в том случае, когда в промежутке (а,b), всего лишь конечное число стационарных точек или точек, где отсутствует конечная производная:
 (1)
(1)
Тогда в любом промежутке

существует конечная производная  и в каждом таком промежутке
и в каждом таком промежутке  сохраняет постоянный знак. Если бы
сохраняет постоянный знак. Если бы  меняла знак, например, в промежутке (xk ,xk+1),то, по теореме Дарбу (Если функция f(x) имеет конечную производную в промежутке [a,b], то функция
меняла знак, например, в промежутке (xk ,xk+1),то, по теореме Дарбу (Если функция f(x) имеет конечную производную в промежутке [a,b], то функция  принимает, в качестве значения, каждое промежуточное число между
принимает, в качестве значения, каждое промежуточное число между  и
и  ), она обращалась бы в нуль в некоторой точке между xk и xk+1,что невозможно, поскольку все корни производной уже содержатся в ряду точек (1).Последнее замечание применимо в некоторых случаях на практике: знак производной
), она обращалась бы в нуль в некоторой точке между xk и xk+1,что невозможно, поскольку все корни производной уже содержатся в ряду точек (1).Последнее замечание применимо в некоторых случаях на практике: знак производной  во всем промежутке ( xk ,,х k +1 ) определится, если вычислить значение (или даже только установить знак) ее в одной какой-либо точке этого промежутка
во всем промежутке ( xk ,,х k +1 ) определится, если вычислить значение (или даже только установить знак) ее в одной какой-либо точке этого промежутка  .
.
При разыскании экстремумов исследование знака производной вблизи испытуемой точки можно заменить исследованием знака второй производной в самой этой точке.
Пусть функция f ( x ) имеет производную f ( x ) в окрестности точки х0, и вторую производную в самой точке х0:  . Точка х0 - стационарная, т.е.
. Точка х0 - стационарная, т.е. 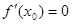 . Если
. Если  , то функция
, то функция  в точке х = х0 возрастает, т.е. вблизи точки х0 слева
в точке х = х0 возрастает, т.е. вблизи точки х0 слева  , а справа
, а справа 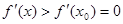 . Таким образом, производная
. Таким образом, производная  меняет знак минус на плюс и, следовательно, f(x) имеет в точке х=х0 минимум. Если, f"(x0)<0, то
меняет знак минус на плюс и, следовательно, f(x) имеет в точке х=х0 минимум. Если, f"(x0)<0, то  в точке х = хо убывает, меняя знак плюс на минус, то имеем максимум.
в точке х = хо убывает, меняя знак плюс на минус, то имеем максимум.
Второе правило для испытания «подозрительного» значения х0: подставляем х0 во вторую производную  :если
:если  , то функция имеет минимум, если же f" (х0) < 0, то - максимум.
, то функция имеет минимум, если же f" (х0) < 0, то - максимум.
Это правило имеет ограничение в применении: оно неприложимо к тем точкам, где не существует конечной первой производной; когда вторая производная обращается в нуль, правило также ничего не дает. Решение вопроса зависит тогда от поведения высших производных.
Замечание. При решении задач практического содержания часто можно не проверять аналитически достаточность условий экстремума (с помощью первой или второй производной). Заключение о наличии экстремума обычно легко сделать на основании условий задачи. Это относится также и к отысканию наибольших и наименьших значений.
План решения текстовых задач на экстремум:
1. Выбрать независимую переменную и установить область её применения.
2. Выразить исследуемую величину через аргумент.
3. Найти стационарные точки и точки, в которых исследуемая функция не имеет производной (в частности, точки, где производная обращается в бесконечность). Из числа последних точек исключить точки несуществования функции.
4. Вычислить значения функции в найденных точках и на концах отрезка изменения аргумента и выбрать из этих значений наибольшее или наименьшее.
Примеры.
1) Нужно построить прямоугольную площадку возле каменной стены так, чтобы с трёх сторон она была огорожена проволочной сеткой, а четвёртой стороной примыкала к стене. Для этого имеется a погонных метров сетки. При каком соотношении сторон площадка будет иметь наибольшую площадь?
Решение
Обозначим стороны площадки x и y. Площадь площадки равна S=xy. По условию, данному в задаче, должно выполняться равенство  . Поэтому
. Поэтому  и
и  , где
, где 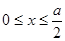 . (Потому что длина и ширина площадки не могут быть отрицательными).
. (Потому что длина и ширина площадки не могут быть отрицательными).
 ,
,  ,
,  ,
, 
Так как  , то при
, то при 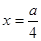 функция S имеет максимум. Значение функции
функция S имеет максимум. Значение функции
S  =
=  кв. ед.
кв. ед.
Так как функция S(x) непрерывна на  и её значения на концах S(0) и S(
и её значения на концах S(0) и S(  ) равны нулю, то найденное значение будет наибольшим значением функции. Таким образом, наиболее выгодным соотношением сторон площадки при данных условиях задачи является
) равны нулю, то найденное значение будет наибольшим значением функции. Таким образом, наиболее выгодным соотношением сторон площадки при данных условиях задачи является 
2) В данный шар вписать цилиндр, имеющий наибольшую боковую поверхность (рис. 6).

Рис. 6
Пусть радиус шара R, а радиус основания цилиндра r. Тогда высота цилиндра h определится по формуле  , а боковая поверхность
, а боковая поверхность  , при этом
, при этом  . Отсюда
. Отсюда  ,
,  при
при  , откуда
, откуда 
Функция S(r) положительна и непрерывна на  . На концах отрезка она равна нулю. Следовательно, внутри отрезка при
. На концах отрезка она равна нулю. Следовательно, внутри отрезка при  она имеет наибольшее значение. Цилиндр такого радиуса будет искомым.
она имеет наибольшее значение. Цилиндр такого радиуса будет искомым.
3) Найти стороны прямоугольника наибольшего периметра, вписанного в полуокружность радиуса R.
Решение
Обозначим стороны прямоугольника через x и y. Тогда периметр равен  . Выразим y через x, зная, что радиус полукруга R (из прямоугольного треугольника):
. Выразим y через x, зная, что радиус полукруга R (из прямоугольного треугольника):
 ,
,  .
.
Тогда периметр

Находим производную:
 , при этом
, при этом 
 при
при 
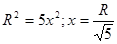

Таким образом, прямоугольник должен иметь стороны  ;
; 
4) Вокруг полушара радиуса описать прямой круговой конус наименьшего объема; при этом предполагается, что основания полушара и конуса лежат в одной плоскости и концентричны (рис. 7).
Решение
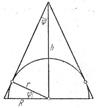
Рис. 7
Обозначим угол при вершине конуса через  . Тогда получается:
. Тогда получается:

И объем конуса: 
Для того чтобы объем V имел наименьшее значение, очевидно, нужно, чтобы выражение у = cos2  sin
sin  , стоящее в знаменателе, получило свое наибольшее значение, при изменении
, стоящее в знаменателе, получило свое наибольшее значение, при изменении  в промежутке
в промежутке  . Имеем
. Имеем

между 0 и  производная обращается в нуль при tg
производная обращается в нуль при tg  =
=  ,
,  , меняя при этом знак плюс на минус. Этот угол доставляет выражению y наибольшее значение, а объёму V – наименьшее.
, меняя при этом знак плюс на минус. Этот угол доставляет выражению y наибольшее значение, а объёму V – наименьшее.
5) Найти для функции  точки максимума, минимума, промежутки возрастания и убывания.
точки максимума, минимума, промежутки возрастания и убывания.

Рис. 8
Решение
Запишем функцию двумя разными формулами для промежутков (  ;0) и [0; +
;0) и [0; +  ). На первом промежутке
). На первом промежутке  , на втором
, на втором  . При
. При  < x < 0 имеем
< x < 0 имеем  . Производная обращается в нуль при х = 1 и х = -1. Первая из этих точек не принадлежит промежутку (
. Производная обращается в нуль при х = 1 и х = -1. Первая из этих точек не принадлежит промежутку (  ; 0). На промежутке (
; 0). На промежутке (  ; - 1) производная положительна, на промежутке (- 1; 0)- отрицательна, поэтому -1 -точка максимума. На промежутке (0;
; - 1) производная положительна, на промежутке (- 1; 0)- отрицательна, поэтому -1 -точка максимума. На промежутке (0;  ) производная у'= Зх2 + 3 > 0, значит функция возрастает на промежутке, и точка x = 0, в которой производная от функции
) производная у'= Зх2 + 3 > 0, значит функция возрастает на промежутке, и точка x = 0, в которой производная от функции  не существует, оказывается точкой минимума. График имеет вид, изображенный на рис. 8.
не существует, оказывается точкой минимума. График имеет вид, изображенный на рис. 8.
6) Миноносец стоит на якоре в 9 км. От ближайшей точки берега; с миноносца нужно послать гонца в лагерь, расположенный в 15 км., считая по берегу от ближайшей к миноносцу точки берега (лагерь расположен на берегу). Если гонец может делать пешком по 5 км/ч, а на вёслах 4 км/ч, то в каком пункте берега он должен пристать, чтобы попасть в лагерь в кратчайшее время?
Решение

Рис. 9
OA=9 км (рис. 9)
OB=15 км
 км/ч
км/ч
 5 км/ч
5 км/ч
Пусть S1 гонец проплывает со скоростью v1=4 км/ч, а путь S2 гонец проходит со скоростью v2=5 км/ч. Пусть OC=x, тогда 


Тогда исследуемая функция будет выглядеть:

Дифференцируя полученную функцию имеем:

 ;
;  ;
;  ;
;  ;
; 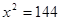
Получаем x = 12 (км). Знак первой производной для значений, несколько меньших 12 и несколько больших 12 меняется с “-” на ”+”, т.е. функция t при x = 12 имеет минимум. Гонец должен доплыть до пункта C, находящемуся на расстоянии 12 км. от пункта O.
|
из
5.00
|
Обсуждение в статье: Максимум и минимум функций |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

