 |
Главная |
Классическая теория электропроводности
|
из
5.00
|
Классическая теория электропроводности объясняет различные свойства вещества существованием и движением в нем электронов, а сами электроны проводимости рассматриваются как электронный газ, подобный идеальному одноатомному газу. При этом предполагается, что движение электронов подчиняется законам классической механики Ньютона.
Взаимодействием электронов между собой пренебрегают и считают, что они взаимодействуют только с положительными ионами решетки. По этой теории электронный газ должен подчиняться законам идеального газа. Согласно закону равномерного распределения энергии по степеням свободы, на один электрон приходится средняя кинетическая энергия теплового движения
Ек = 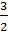 kT, (4.1)
kT, (4.1)
гдеk– постоянная Больцмана, Т – температура.
При тепловом движении электроны испытывают соударения. Путь, проходимый электронами между двумя последовательными соударениями, называют длиной свободного пробега 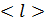 .
.
Предполагается, что при каждом соударении электрон полностью передает свою энергию ионам решетки и начальная скорость последующего движения электрона равна нулю.
Если по проводнику течет постоянный ток, то внутри проводника существует электрическое поле напряженностью Е. На каждый электрон со стороны электрического поля действует сила F= еЕ, где е – заряд электрона. Под действием этой силы электрон приобретает ускорение а, которое можно определить из равенства mea = еЕ, откуда
а = 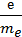 E
E
(me – масса электрона)
Если 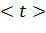 - [U2] среднее время между двумя последовательными соударениями, то к концу свободного пробега электрон приобретает скорость
- [U2] среднее время между двумя последовательными соударениями, то к концу свободного пробега электрон приобретает скорость 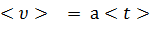 =
= 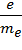 E
E 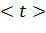 . Средняя скорость упорядоченного движения электронов
. Средняя скорость упорядоченного движения электронов
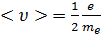 E
E 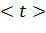 (4.2)
(4.2)
(начальная скорость полагается равной нулю, поэтому движение считается равноускоренным).
Среднее время между двумя последовательными соударениями можно определить, если знать длину свободного пробега и среднюю скорость теплового движения 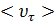 :
:
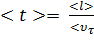 . (4.3)
. (4.3)
Вообще, 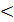 t
t 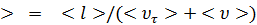 , но соотношение (4.3) справедливо, так как
, но соотношение (4.3) справедливо, так как 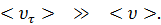
Подставив 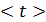 из формулы (4.3) в формулу (4.2) получим
из формулы (4.3) в формулу (4.2) получим
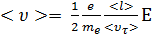 . (4.4)
. (4.4)
Известно, что плотность j тока в проводнике пропорциональна концентрации n свободных электронов в нем и скорости их движения 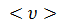
j = ne 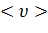 . (4.5)
. (4.5)
Подставив (4.4) в (4.5), получим
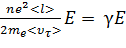 (4.6)
(4.6)
где
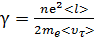 (4.7)
(4.7)
–[U3] удельная проводимость материала проводника (величина, обратная его удельному сопротивлению).
Из выражения (4.6), представляющего закон Ома, следует: плотность тока пропорциональна напряженности электрического поля, что совпадает с законом Ома в дифференциальной форме.
Из формулы (4.6) легко получить закон Ома в виде I = U / R, для этого ее правую и левую части надо умножить на S – площадь поперечного сечения проводника. Учитывая, что  E = U / I (поле внутри проводника считаем однородным); следовательно,
E = U / I (поле внутри проводника считаем однородным); следовательно,
I = 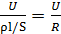 .
.
На основании электронной теории электропроводимости металлов можно объяснить зависимость сопротивления проводников от температуры. С повышением температуры его удельное сопротивление увеличивается, а электропроводимость уменьшается. Анализируя выражение (4.7), видим, что электропроводимость пропорциональна концентрации n электронов проводимости и средней длине свободного пробега 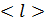 , т.е. чем больше длина свободного пробега
, т.е. чем больше длина свободного пробега 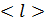 , тем меньшую помеху для упорядоченного движения электронов представляют соударения. Электропроводимость обратно пропорциональна средней тепловой скорости движения. Тепловая скорость
, тем меньшую помеху для упорядоченного движения электронов представляют соударения. Электропроводимость обратно пропорциональна средней тепловой скорости движения. Тепловая скорость 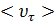 при повышении температуры возрастает пропорционально
при повышении температуры возрастает пропорционально  что приводит к уменьшению электропроводимости и увеличению удельного сопротивления проводников. Анализируя формулу (4.7) можно, кроме того, объяснить зависимость
что приводит к уменьшению электропроводимости и увеличению удельного сопротивления проводников. Анализируя формулу (4.7) можно, кроме того, объяснить зависимость  и
и 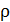 от рода проводника.
от рода проводника.
На основании классической электронной теории проводимости металлов можно объяснить закон Джоуля – Ленца.
Упорядоченное движение электронов происходит под действием сил поля. Как было сказано выше, будем считать, что в момент соударения с положительными ионами кристаллической решетки электроны полностью передают ей свою кинетическую энергию. К концу свободного пробега скорость электрона 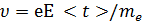 , а кинетическая энергия
, а кинетическая энергия
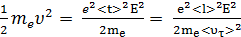 .
.
Мощность, выделяемая единицей объема металла (плотность мощности), равна произведению энергии одного электрона на число соударений в секунду 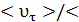 l
l 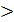 и на концентрацию n электронов:
и на концентрацию n электронов:
ω = 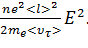 (4.8)
(4.8)
Учитывая (4.7) имеем
ω = 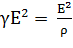 (4.9)
(4.9)
– закон Джоуля – Ленца в дифференциальной форме.
Классическая электронная теория оказалась бессильной объяснить ряд экспериментальных фактов.
Из опыта известно, что удельное сопротивление металлов в широком температурном интервале пропорционально абсолютной температуре (ρ ~ Т), в то время как электронная теория предсказывает иную зависимость ρ отТ, а именно ρ ~ 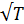 .
.
По классической электронной теории атомная теплоемкость диэлектриков должна быть в 1,5 раз меньше, чем атомная теплоемкость металлов. Однако опытный закон Дюлонга и Пти показывает, что атомная теплоемкость всех одноатомных кристаллов (и диэлектриков, и металлов) составляет приблизительно 3R, где R –универсальная газовая постоянная.
По классической электронной теории атомная теплоемкость металлов будет складываться из теплоемкости решетки (3R) и теплоемкости электронного газа (  ):
):
( 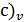 = 3R +
= 3R +  =
= 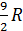 .
.
Следовательно, опытные данные показывают, что при нагревании металлов энергия теплового движения свободных электронов практически не изменяется, т.е. электроны не участвуют в накоплении сообщаемой проводнику энергии. Всю сообщаемую проводнику энергию аккумулирует кристаллическая решетка
Для объяснения электропроводности металлов в классической электронной теории было сделано предположение, что электроны свободно пробегают лишь расстояния между соседними узлами решетки. Для согласования теоретических и экспериментальных значений электропроводности металлов, приходится предположить, что свободные электроны пробегают без столкновений с ионами решетки расстояния, превосходящие расстояние между ионами в десятки и даже в сотни раз (чем ниже температура, тем больше эти расстояния).
Дальнейшее развитие классической электронной теории не привели к разрешению возникших противоречий с экспериментом. Только с созданием квантовой электронной теории металлов эти противоречия были разрешены.
В основе квантовой теории металлов лежат принципиально новые (по сравнению с классической теорией) идеи.
В квантовой электронной теории металлов предполагается, что электрон имеет двойственную, корпускулярно-волновую природу. Если по классическим представлениям электрон является частицей с резко очерченными границами, которая движется по вполне определенной траектории, причем положение его в пространстве и скорость движения могут быть одновременно и однозначно определены, то по квантовым представлениям электрон обладает кроме корпускулярных свойств еще и волновыми. В результате движение электрона в пространстве следует представлять как процесс распространения своеобразной электронной волны, способной к интерференции, дифракции. Понятие траектории к электронам и другим микрочастицам неприменимо. Невозможно также одновременное и точное определение положения электрона и скорости.
Квантовая теория предполагает, что энергия свободных электронов в металле может принимать не любые, а только некоторые дискретные значения, изменения ее могут происходить не непрерывно, а лишь скачком, сразу на вполне определенную величину, в то время как классическая электронная теория металлов постулирует, что энергия свободных электронов в металле может изменяться непрерывно и на любую величину, может принимать какие угодно значения.
|
из
5.00
|
Обсуждение в статье: Классическая теория электропроводности |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

