Поиск по графу в ширину

Рассмотрим теперь поиск в ширину.  При поиске в ширину "правила игры" такие: достигнув некоторой вершины v, отмечаем ее. Затем просматриваем ее список смежности L[v] и отмечаем все ранее не отмеченные вершины списка (при старте поиска v = v0). После того как отмечены все вершины из L[v], вершину v считаем полностью обработанной и продолжаем обработку вершин из списка L[v]по очереди согласно описанным правилам.

Именно в обработке сразу всего списка смежности текущей вершины заключается принципиальное отличие поиска в ширину от поиска в глубину: там мы "ныряли" как можно "глубже", а здесь идем с "бреднем", "загребая" сразу все, что можно.

Поиск в ширину заканчивается, когда все вершины полностью обработаны или продолжение поиска невозможно.

Возьмем неориентированный и ориентированный графы предыдущего примера и рассмотрим для них поиск в ширину (рис. 4.2).

Рис. 4.2.

Для неориентированного графа (см. рис. 4.2,а) поиск из стартовой вершины v0 будем осуществлять так. Стартовой вершине присвоим номер 1. Затем пронумеруем все вершины из списка смежности стартовой вершины в порядке следования их в списке. При этом вершина  v1получит номер 2, а вершина v3— номер 3.

Теперь, когда все вершины из списка смежности вершины v0 отмечены, перейдем в первую по очереди вершину  v1. В ее списке смежности только одна ранее не отмеченная вершина — v2. Присвоим ей номер 4 и перейдем в вершину v3. На этом этапе номер 5 получит вершина v4, а номер 6 — вершина v5.

Затем перейдем в вершину v2. Поскольку все вершины из списка смежности вершины v2 уже отмечены, перейдем в вершину v4. Здесь также все вершины из списка смежности отмечены, поэтому перейдем в вершину v5.

Просмотрим неотмеченные вершины из ее списка смежности и отметим вершины v6 и  v7, присваивая им номера 7 и 8 соответственно. Теперь, когда список смежности вершины v6 обработан полностью, перейдем в вершину v6. Так как в ее списке смежности нет неотмеченных вершин, перейдем в вершину v7. Здесь также в списке смежности нет неотмеченных вершин. Все вершины обработаны, и поиск в ширину для графа закончен.

Результаты поиска в ширину из вершины v0 в ориентированном графе представлены на рис.4.2,б.

Обратим внимание на то, что нумерация вершин при поиске в ширину отличается от нумерации вершин при поиске в глубину. Так, в ориентированном графе на рис. 4.2,б мы сразу отмечаем оба элемента списка смежности вершины v0. Поэтому вершине, получившей при поиске в глубину номер 4, при поиске в ширину присваивается номер 3.

Лекция 5. Поиск кратчайшего пути между вершинами графа.

Основные положения

Предполагаем, что имеем простой взвешенный ориентированный граф.

Определение. Сумму весов ребер пути будем называть весом или длиной этого пути.

Определение. Алгоритм Э. Дейкстры находит кратчайшее расстояние от одной из вершин графа до всех остальных.

Алгоритм работает только для графов без рёбер отрицательного веса. Алгоритм широко применяется в программировании и технологиях, например, его использует протокол OSPF для устранения кольцевых маршрутов.

Рассмотрим два примера применения алгоритма Дейкстры на практике.

Вариант 1. Дана сеть автомобильных дорог, соединяющих города Новосибирской области. Найти кратчайшие пути от Новосибирска до каждого города области (если двигаться можно только по дорогам).

Вариант 2. Имеется некоторое количество авиарейсов между городами мира, для каждого известна стоимость. Найти маршрут минимальной стоимости (возможно, с пересадками) от Копенгагена до Барнаула.

Алгоритм Дейкстры

Дан простой взвешенный графG(V, E) без петель и дуг отрицательного веса. Найти кратчайшие пути от некоторой вершины a графа G до всех остальных вершин этого графа.

1. Каждой вершине из V сопоставим метку — минимальное известное расстояние от этой вершины до a . Алгоритм работает пошагово — на каждом шаге он «посещает» одну вершину и пытается уменьшать метки. Работа алгоритма завершается, когда все вершины посещены.

2. Инициализация. Метка самой вершины a полагается равной 0, метки остальных вершин — бесконечности. Это отражает то, что расстояния от a до других вершин пока неизвестны. Все вершины графа помечаются как не посещенные.

3. Шаг алгоритма. Если все вершины посещены, алгоритм завершается. В противном случае из еще не посещенных вершин выбирается вершина u , имеющая минимальную метку. Мы рассматриваем всевозможные маршруты, в которых u является предпоследним пунктом. Вершины, соединенные с вершиной u ребрами, назовем соседями этой вершины. Для каждого соседа рассмотрим новую длину пути, равную сумме текущей метки u и длины ребра, соединяющего u с этим соседом. Если полученная длина меньше метки соседа, заменим метку этой длиной. Рассмотрев всех соседей, пометим вершину u как посещенную и повторим шаг.

  Рассмотрим выполнение алгоритма на примере графа, показанного на рисунке 5.1. Пусть требуется найти расстояния от 1-й вершины до всех остальных.

Рис. 5.1

Кружками обозначены вершины, линиями — пути между ними (ребра графа). В кружках обозначены номера вершин, над ребрами обозначена их «цена» — длина пути. Рядом с каждой вершиной красным обозначена метка — длина кратчайшего пути в эту вершину из вершины 1.

Первый шаг. Рассмотрим шаг алгоритма Дейкстры для нашего примера. Минимальную метку имеет вершина 1. Ее соседями являются вершины 2, 3 и 6.

Первый по очереди сосед вершины 1 — вершина 2, потому что длина пути до нее минимальна. Длина пути в нее через вершину 1 равна кратчайшему расстоянию до вершины 1 + длина ребра, идущего из 1 в 2, то есть 0 + 7 = 7. Это меньше текущей метки вершины 2, поэтому новая метка 2-й вершины равна 7. На графике изначально рассмотрена вершина №3.

Аналогичную операцию проделываем с двумя другими соседями 1-й вершины — 3-й и 6-й.

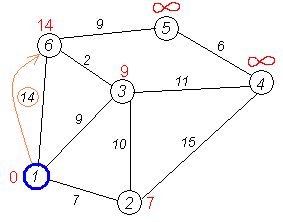
Все соседи вершины 1 проверены. Текущее минимальное расстояние до вершины 1 считается окончательным и пересмотру не подлежит (то, что это действительно так, впервые доказал Дейкстра). Вычеркнем её из графа, чтобы отметить, что эта вершина посещена.

Второй шаг'. Шаг алгоритма повторяется. Снова находим «ближайшую» из непосещенных вершин. Это вершина 2 с меткой 7.

Снова пытаемся уменьшить метки соседей выбранной вершины, пытаясь пройти в них через 2-ю. Соседями вершины 2 являются 1, 3, 4.

Первый (по порядку) сосед вершины 2 — вершина 1. Но она уже посещена, поэтому с 1-й вершиной ничего не делаем.

Следующий сосед вершины 2 — вершина 4. Если идти в неё через 2-ю, то длина такого пути будет = кратчайшее расстояние до 2 + расстояние между вершинами 2 и 4 = 7 + 15 = 22. Поскольку 22< , устанавливаем метку вершины 4 равной 22.

Ещё один сосед вершины 2 — вершина 3. Если идти в неё через 2, то длина такого пути будет = 7 + 10 = 17. Но текущая метка третьей вершины равна 9<17, поэтому метка не меняется.

Все соседи вершины 2 просмотрены, замораживаем расстояние до неё и помечаем ее как посещенную.

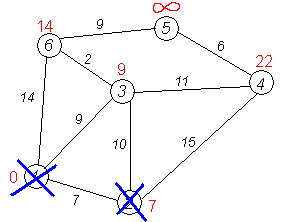
Третий шаг. Повторяем шаг алгоритма, выбрав вершину 3. После ее «обработки» получим такие результаты:

Дальнейшие шаги. Повторяем шаг алгоритма для оставшихся вершин (Это будут по порядку 6, 4 и 5).

Завершение выполнения алгоритма. Алгоритм заканчивает работу, когда вычеркнуты все вершины. Результат его работы виден на последнем рисунке: кратчайший путь от вершины 1 до 2-й составляет 7, до 3-й — 9, до 4-й — 20, до 5-й — 20, до 6-й — 11.

Применим алгоритм Дейкстры для графа Рис. 5.2. от вершины А.

Рис. 5.2

    Алгоритмы поиска пути на графе различаются также направлением поиска. Существуют прямые, обратные и двунаправленные методы поиска.

Двунаправленный поиск требует удовлетворительного решения двух проблем: смены направления поиска и оптимизации "точки встречи".

Одним из критериев для решения первой проблемы является сравнение "ширины" поиска в обоих направлениях - выбирается то направление, которое сужает поиск.

Вторая проблема вызвана тем, что прямой и обратный пути могут разойтись и, чем уже поиск, тем это более вероятно.

Рассмотрим жадный алгоритма поиска кратчайшего пути при обходе всех вершин графа.

Рис. 5.3

Пусть вершина 6 – вершина начала прохода, тогда путь с минимальным общим весом будет следующим:

å = 1,7