 |
Главная |
Сборник основных правил комбинаторики и упражнений для их применения
|
из
5.00
|
Примеры комбинаторных задач
Пример 1. Из группы теннисистов, в которую входят четыре человека – Антонов, Григорьев, Сергеев и Федоров, тренер выделяет пару для участия в соревнованиях. Сколько существует вариантов выбора такой пары?
Решение: Составим сначала все пары, в которые входит Антонов (для краткости будем писать первые буквы фамилий). Получим три пары: АГ, АС, АФ.
Выпишем теперь пары, в которые входит Григорьев, но не входит Антонов. Таких пар две: ГС, ГФ.
Далее составим пары, в которые входит Сергеев, но не входят Антонов и Григорьев. Такая пара только одна: СФ.
Других вариантов составления пар нет, так как все пары, в которые входит Федоров уже составлены.
Итак, мы получили 6 пар:
АГ, АС, АФ
ГС, ГФ
СФ,
т.е. 3·2·1=6. значит, существует всего шесть вариантов выбора тренером пары теннисистов из данной группы.
Способ рассуждений, которым мы воспользовались при решении задачи, называют перебором возможных вариантов.
Пример 2. Сколько трехзначных чисел можно составить из цифр 1, 3, 5, 7, используя в записи числа каждую из них не более одного раза?
При решении этой задачи сначала составляется древо всех возможных вариантов.
| Первая цифра | 1 | 3 | 5 | 7 | ||||||||||||||||||||
| Вторая цифра |
3 |
5 |
7 |
1 |
5 |
7 |
1 |
3 |
7 |
1 |
3 |
5 | ||||||||||||
| Третья цифра | 5 | 7 | 3 | 7 | 3 | 5 | 5 | 7 | 1 | 7 | 1 | 5 | 3 | 7 | 1 | 7 | 1 | 3 | 3 | 5 | 1 | 5 | 1 | 3 |
Заметим, что ответ на поставленный в примере вопрос можно получить, не выписывая сами числа и не строя дерево возможных вариантов. Рассуждать будем так. Первую цифру трехзначного числа можно выбрать четырьмя способами. Так после выбора первой цифры останутся три, то вторую цифру можно выбрать из оставшихся цифр уже тремя способами. Наконец, третью цифру можно выбрать (из оставшихся двух) двумя способами. Следовательно, общее число искомых трехзначных чисел равно произведению 4·3·2 = 24.
Ответ на поставленный в примере 2 вопрос мы нашли, используя так называемое комбинаторное правило умножения.
Пусть имеется n элементов и требуется выбрать один за другим некоторые k элементов. Если первый элемент можно выбрать n1 способами, после чего второй элемент можно выбрать из оставшихся n2 способами, затем третий элемент – n3 способами и т.д., то число способов, которыми могут быть выбраны все k элементов, равно произведению n1·n2·n3·…·nk.
Пример 3. Из города А в город В ведут две дороги, из города В в город С – три дороги, из города С до пристани – две дороги (рис. 1). Туристы хотят проехать из города А через города В и С к пристани. Сколькими способами они могут выбрать маршрут?

А В С Пристань Рис. 1
Решение. Путь из А в В туристы могут выбрать двумя способами. Далее в каждом случае они могут проехать из В в С тремя способами. Значит, имеется 2·3 вариантов маршрута из А в С. Так как из города С на пристань можно попасть двумя способами, то всего существует 2·3·2, т.е. 12 способов выбора туристами маршрута из города А к пристани.
Упражнения в данном пункте направлены на составление различных комбинаций и подсчет числа возможных вариантов этих комбинаций.
Упражнения
5. В кафе предлагают два первых блюда: борщ, рассольник – и четыре вторых блюда: гуляш, котлеты, сосиски, пельмени. Укажите все обеды из двух блюд, которые может заказать посетитель. Проиллюстрируйте ответ, построив дерево возможных вариантов.
6. Имеется белый хлеб, черный хлеб, сыр, колбаса и варенье. Сколько видов бутербродов можно приготовить?
7. На тарелке лежат 5 яблок и 4 апельсина. Сколькими способами можно выбрать один плод?
Решение. По условию задачи яблоко можно выбрать пятью способами, апельсин – четырьмя. Так как в задаче речь идет о выборе «либо яблоко, либо апельсин», то его, согласно правилу суммы, можно осуществить 5 + 4 = 9 способами.
8. На тарелке лежат 5 яблок и 4 апельсина. Сколькими способами можно выбрать пару плодов, состоящую из яблока и апельсина?
Решение: По условию задачи яблоко можно выбрать пятью способами, апельсин – четырьмя. Так как в задаче речь идет о выборе пары (яблоко, апельсин), то ее, согласно правилу произведения, можно выбрать 5·4=20 способами.
9. Сколько всего двузначных чисел можно составить из цифр 7, 4 и 5 при условии, что они в записи числа не повторяются?
Решение: чтобы записать двузначное число, надо выбрать цифру десятков и цифру единиц. Согласно условию на месте десятков в записи может быть любая из цифр 7, 4 и 5. другими словами, выбрать цифру десятков можно тремя способами. После того, как цифра десятков определена, для выбора цифры единиц остается две возможности, цифры в записи числа не должны повторяться. Так как любое двузначное число – это упорядоченная пара, состоящая из цифр десятков и цифр единиц, то ее выбор, согласно правилу произведения, можно осуществить 3·2=6 способами.
10. Сколько трехзначных чисел можно составить, используя цифры 7, 4 и 5?
Решение: в данной задаче рассматриваются трехзначные числа, так как цифры в записи этих чисел могут повторяться, то цифру сотен, цифру десятков и цифру единиц можно выбрать тремя способами каждую. Поскольку запись трехзначного числа представляет собой упорядоченный набор из трех элементов, то, согласно правилу произведения, его выбор можно осуществить 3·3·3=27 способами.
11. Сколько всего четырехзначных чисел можно составить из цифр 0 и 3?
Решение: Запись четырехзначного числа представляет собой упорядоченный набор (кортеж) из четырех цифр. Первую цифру – цифру тысяч можно выбрать только одним способом, так как запись числа не может начинаться с нуля. Цифрой сотен может быть либо ноль, либо три, т.е. имеется два способа выбора. Цифру десятков можно выбрать двумя способами, цифру единиц – двумя. Чтобы узнать, сколько всего четырехзначных чисел можно составить из цифр 0 и 3, согласно правилу произведения, способы выбора каждой цифры надо перемножить: 1·2·2·2=8. таким образом, имеем 8 четырехзначных чисел.
12. Сколько трехзначных чисел можно записать, используя цифры 0, 1, 3, 6, 7 и 9, если каждая из них может быть использована в записи только один раз?
Решение: Так как запись числа не может начинаться с нуля, то цифру сотен можно выбрать пятью способами; выбор можно также осуществить пятью способами, поскольку цифры в записи числа не должны повторяться, а одна из шести цифр будет уже использована для записи сотен; после выбора двух цифр (для записи сотен и десятков) выбрать цифру единиц из данных шести можно четырьмя способами. Отсюда, по правилу произведения, получаем, что трехзначных чисел можно образовать 5·5·4 = 100 способами.
13. У Ирины пять подруг: Вера, Зоя, Марина, Полина и Светлана. Она решила двух из них пригласить в кино укажите все возможные варианты выбора подруг. Сколько таких вариантов?
14. Сколько можно составить пар, выбирая:
а) первый предмет из 4, а второй из 8;
б) первый предмет из 6, а второй из 3;
в) первый предмет из 15, а второй из 12;
15. В школе есть все классы с 1 по 11. каждый из них имеет дополнительную букву «а», «б», «в», «г» или «д». сколько всего классов в этой школе?
16. на каждом барабане игрального автомата изображены символы: «вишня», «лимон» и числа от 1 до 9. автомат имеет три одинаковых барабана, которые вращаются независимо друг от друга. Сколько всего комбинаций может выпасть?
17. Первый класс праздновал Новый год. Каждая девочка подарила каждому мальчику открытку, а каждый мальчик подарил каждой девочке гвоздику. Чего было больше – подаренных открыток или подаренных гвоздик?
18. Стадион имеет 4 входа: А, В, С и Д. укажите все возможные способы, какими посетитель может войти через один вход и выйти через другой. Сколько таких способов?
19. Укажите все способы, какими можно разложить три яблока в две вазы (учтите при этом случаи, когда одна из ваз окажется пустой).
20. Составьте все возможные двузначные числа, используя в записи указанные цифры не более одного раза:
а) 1, 6, 8; б)0, 3, 4.
21. Из цифр 1, 2, 3 составьте все возможные двузначные числа при условии, что:
а) цифры в числе не повторяются;
б) допускается повторение цифр в числе.
22. Используя цифры 0, 2, 4, 6, составьте все возможные трехзначные числа, в которых цифры не повторяются.
23. В шахматном турнире участвуют 9 человек. Каждый из них сыграл с каждым по одной партии. Сколько всего партий было сыграно?
24. В соревнованиях по футболу участвовало 12 команд. Каждая команда провела с каждой из остальных по одной игре на своем поле и по одной игре на поле соперника. Сколько всего игр было сыграно?
25. При встрече 8 человек обменялись рукопожатиями. Сколько всего было сделано рукопожатий?
26. Учащиеся 6 класса решили обменяться фотографиями. Сколько фотографий для этого потребуется, если в классе 24 человека?
27. На входной двери дома установлен домофон, на котором нанесены цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. каждая квартира получает кодовый замок из двух цифр типа 0-2, 3-7, 7-3, 8-8 и т.п., позволяющий открывать входную дверь. Хватит ли кодовых замков для всех квартир дома, если в доме 96 квартир?
28. Из села Дятлово в село Матвеевское ведут три дороги, а из села Матвеевское в село Першино – четыре дороги. Сколькими способами можно попасть из Датлова в Першино через Матвеевское?
29. В кафе имеются три первых блюда, пять вторых блюд и два третьих. Сколькими способами посетитель кафе может выбрать ответ, состоящий из первого, второго и третьего блюд?
Решение. Первое блюдо можно выбрать 3 способами. Для каждого выбора первого блюда существует 5 возможностей выбора второго блюда. Значит, первые два блюда можно выбрать 3·5 способами. Наконец, для каждого выбора третьего блюда, т.е. существует 3·5·2 способов составления обеда из трех букв. Итак, обед из трех букв может быть составлен 30 способами.
30. Петр решил пойти на новогодний карнавал в костюме мушкетера. В ателье проката ему предложили на выбор различные по фасону и цвету предметы: пять пар брюк, шесть камзолов, три шляпы и две пары сапог. Сколько различных карнавальных костюмов можно составить из этих предметов?
Перестановки
Простейшими комбинациями, которые можно составить из элементов конечного множества являются перестановки.
Рассмотрим пример 1. Пусть имеются три книги. Обозначим их буквами a, b, c. Эти книги можно расставить на полке по-разному:
abc, acb, bac, bca, cab, cba.
Каждое из этих расположений называют перестановкой из трех элементов.
Перестановкой из n элементов называется каждое расположение этих элементов в определенном порядке.
Число перестановок из n элементов обозначается символом Pn (читается «Р из n»).
Мы установили, что Р3 = 6. для того, чтобы найти число перестановок из трех элементов, можно не выписывать эти перестановки, а воспользоваться правилом умножения. Будем рассуждать так. На первое место можно поставить любой из трех элементов. Для каждого выбора первого элемента есть две возможности выбора второго из оставшихся двух элементов. Наконец, для каждого выбора первых двух элементов остается единственная возможность выбора третьего элемента. Значит, число перестановок из трех элементов равно 3·2·1, т.е. 6.
Выведем теперь формулу для числа перестановок из п элементов.
Пусть мы имеем n элементов. На первое место можно поставить любой из них. Для каждого выбора первого элемента на второе место можно поставить один из оставшихся n-1 элементов. Для каждого выбора первых двух элементов на третье место можно поставить один из оставшихся n-2 элементов и т.д. в результате получим, что
Pn = n(n-1)(n-2) ·…·3·2·1.
Расположив множители в порядке возрастания, получим
Pn = 1·2·3·…·( n -2)( n -1) n .
Для произведения первых n натуральных чисел используется специальное обозначение: n! (читается «n факториал»).
Таким образом, число всевозможных перестановок из n элементов вычисляется по формуле Pn = n !
Например, 2!=1·2=2; 5!=1·2·3·4·5=120.
По определению считают, что 1!=1.
Применение данной формулы иллюстрируется в пособии следующими примерами.
Пример 2. Сколькими способами могут быть расставлены 8 участниц финального забега на восьми беговых дорожках?
Число способов равно числу перестановок из 8 элементов. По формуле числа перестановок находим, что Р8 = 8!= 1 · 2 · 3 · 4 · 5 · 6 · 7 · 8 = 40320.
Значит, существует 40320 способов расстановки участниц забега на восьми беговых дорожках.
Пример 3. Сколько различных четырехзначных чисел, в которых цифры не повторяются, можно составить из цифр 0, 2, 4, 6?
Из цифр 0, 2, 4, 6 можно получить Р4 перестановок. Из этого числа надо исключить те перестановки, которые начинаются с 0, т.к. натуральное число не может начинаться с цифры 0. число таких перестановок равно Р3. значит, искомое число четырехзначных чисел (без повторения цифр), которые можно составить из цифр 0, 2, 4, 6, равно Р4 – Р3. Получаем, Р4 – Р3 = 4! – 3! = 24 – 6 = 18.
Пример 4. Имеется девять различных книг, четыре из которых – учебники. Сколькими способами можно расставить эти книги на полке так, чтобы все учебники стояли рядом?
Сначала будем рассматривать учебники как одну книгу. Тогда на полке надо расставить не 9, а 6 книг это можно сделать Р6 способами. В каждой из полученных комбинаций можно выполнить Р4 перестановок учебников. Значит, искомое число способов расположения книг на полке равно произведению Р6·Р4 = 6! ·4! = 720·24 = 17280.
Упражнения
31. Сколькими способами 4 человека могут разместиться на четырехместной скамейке?
32. Курьер должен разнести пакеты в 7 различных учреждений. Сколько маршрутов он может выбрать?
33. Сколькими способами 9 человек могут встать в очередь в театральную кассу?
34. В автосервис одновременно приехали 3 машины для ремонта. Сколько существует способов выстроить их в очередь на обслуживание?
35. Сколько есть способов раздать спортивные номера с 1 по 5 пяти хоккеистам?
36. Сколько существует выражений тождественно равных произведению аbcde, которые получаются из него перестановкой множителей?
37. Ольга помнит, что телефон подруги оканчивается цифрами 5, 6, 7, но забыла в каком порядке эти цифры следуют. Укажите наибольшее число вариантов, которые ей придется перебрать, чтобы дозвониться подруге.
38. Сколько шестизначных чисел (без повторения цифр) можно составить из цифр:
а) 1, 2, 5, 6, 7, 8; б) 0, 2, 5, 6, 7, 8?
39. Сколько среди четырехзначных чисел (без повторения цифр), составленных из цифр 3, 5, 7, 9, таких, которые:
а) начинаются с цифры 3; б) кратны 15?
40. Найдите сумму цифр всех четырехзначных чисел, которые можно составить из цифр 1, 3, 5, 7 (без их повторения).
41. Сколько чисел (без повторения цифр) можно составить из цифр 1, 2, 3, 4, таких которые:
а) больше 3000; б) больше 2000?
42. Семь мальчиков, в число которых входят Олег и Игорь, становятся в ряд. Найдите число возможных комбинаций, если:
а) Олег должен находиться в конце ряда;
б) Олег должен находиться в начале ряда, а Игорь – в конце;
в) Олег и Игорь должны стоять рядом.
Решение. а) так как место Олега фиксировано, то число комбинаций зависит от расположения остальных шести мальчиков. Значит число комбинаций равно Р6=6!=1·2·3·4·5·6=720.
б) Так как места Олега и Игоря фиксированы, то число комбинаций зависит от расположения пяти остальных мальчиков, т.е. равно Р5=5!=1·2·3·4·5=120.
в) Будем рассматривать пару Олег-Игорь как один элемент. Расположение этой пары и пяти остальных мальчиков может быть выполнено Р6=6! способами. В каждой из этих комбинаций Олег и Игорь могут располагаться Р2=2! Способами. Значит искомое число способов расположения мальчиков равно Р6·Р2=6! ·2!=720·2=1440.
43. В расписании на понедельник шесть уроков: алгебра, геометрия, биология, история, физкультура, химия. Сколькими способами можно составить расписание на этот день так, чтобы два урока математики (алгебра и геометрия) стояли рядом?
44. Сколько существует перестановок букв слова «конус», в которых буквы к, о, н стоят рядом?
45. Сколькими способами можно расставить на полке 12 книг, из которых 5 книг – это сборники стихов, так, чтобы сборники стихов стояли рядом?
46. Сколькими способами 5 мальчиков и 5 девочек могут занять в театре в одном ряду места с 1 по 10? Сколькими способами они могут это сделать, если мальчики будут сидеть на нечетных местах, а девочки – на четных?
Решение. Если мальчики и девочки сядут в один ряд в произвольном порядке, то это можно сделать Р10=10!=3628800 способами. Если мальчики сядут на нечетные места, то существуют Р5 способов их расположения. Столькими же способами могут расположиться девочки на четных местах. Каждому способу расположения мальчиков соответствует Р5 способов расположения девочек. Значит, расположиться так, что мальчики будут сидеть на нечетных местах, а девочки – на четных, можно Р5·Р5=5! ·5!=120·120=14400 способами.
47. Делится ли число 30! на:
а) 90; б) 92; в)94; г) 96?
Решение. а) 90=2·5·9. Среди множителей числа 30! есть числа 2, 5 и 9. значит, число 30! делится на 90.
б) 92=4∙23. Среди множителей 30! есть числа 4, 23. Значит, число 30! делится на 92.
в) 94=2·47. Число 47 простое и больше, чем 30. Так как среди множителей числа 30! нет числа 47, то число 30! не делится на 94.
г) 96=2·3·16. Среди множителей 30! есть числа 2, 3, 16. Значит, число 30! делится на 96.
48. Делится ли число 14! на:
а) 168; б) 136; в) 147; г) 132?
49. Найдите значение выражения:
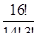 а)
а) 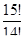 б)
б) 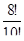 в)
в) 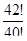 г)
г) 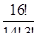
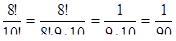 Решение: а)
Решение: а) 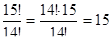 б)
б) 
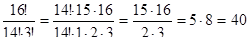 в)
в) 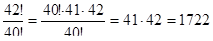 г)
г) 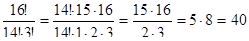
50. Вычислите значение дроби:
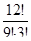 а)
а) 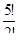 ; б)
; б) 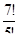 ; в)
; в) 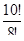 ; г)
; г) 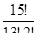 ; д)
; д) 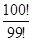 ; е)
; е) 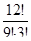
51. Выпишите все натуральные делители числа:
а) 4!; б) 5!; в)6!
52. Докажите, что если n<m, то m! делится на n! без остатка.
53. Что больше и во сколько раз:
а) 6!∙5 или 5! ∙6 б) (п+1)! ∙п или п! ∙(п+1)
Размещения
Пусть имеется 4 шара и 3 пустых ячейки. Обозначим шары буквами a, b, c, d. в пустые ячейки можно по-разному разместить три шара из этого набора шаров. Если мы поместим шар a в первую ячейку, шар b во вторую, а шар с в третью ячейку, то получим одну из возможных упорядоченных троек шаров:
| a | b | c |
Выбирая по-разному первый, второй и третий шары, будем получать различные упорядоченные тройки шаров, например:
| a | c | b | b | a | c | a | b | c |
Каждую упорядоченную тройку, которую можно составить из четырех элементов, называют размещением четырех элементов по три.
После этого дается определение и вводится соответствующее обозначение.
Размещением из n элементов по k (k ≤ n) называется любое множество, состоящее из любых k элементов, взятых в определенном порядке из данных n элементов.
Число размещений из n элементов по k обозначают 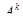 (читают «А из n по k»).
(читают «А из n по k»).
Из определения следует, что два размещения из п элементов по k считаются различными, если они отличаются самими элементами или порядком их расположения.
Составим из элементов a, b, с, d все размещения по три элемента. В первой строке запишем все размещения, которые начинаются с элемента a, во второй – с элемента b, в третьей – с элемента c, в четвертой – с элемента d. Получим такую таблицу:
abc, abd, acb, acd, adb, adc,
bac, bad, bca, bcd, bda, bdc,
cab, cad, cba, cbd, cda, bdc,
dab, dac, dba, dbc, dca, dcb.
Из составленной таблицы видно, что 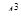 =24.
=24.
Число размещений из четырех элементов по три можно найти, не выписывая самих размещений. Первый элемент можно выбрать четырьмя способами, так как им может быть один из четырех элементов. Для каждого выбранного первого элемента можно тремя способами выбрать второй элемент из трех оставшихся. Наконец, для каждых первых двух элементов можно двумя способами выбрать из двух оставшихся третий элемент. В результате получаем, что 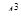 =4·3·2=24.
=4·3·2=24.
Приведенный способ рассуждений используем для вывода формулы числа размещений из n элементов по k, где n≤ k.
Первый элемент можно выбрать n способами. Так как после этого остается n-1 элементов, то для каждого выбора первого элемента можно n-1 способами выбрать второй элемент. Далее, для каждого выбора первых двух элементов можно n-2 способами выбрать третий элемент (из n-2 оставшихся). Наконец, для каждого выбора первых k-1 элементов можно n – (k – 1) способами выбрать k-й элемент (из n – (k -1) оставшихся).
Значит, 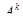 = n ( n – 1)( n – 2)∙…∙( n – ( k – 1))
= n ( n – 1)( n – 2)∙…∙( n – ( k – 1))
Мы получили формулу для вычисления числа размещений из п элементов по k.
Например, число размещений из шестнадцати элементов по пять равно произведению пяти множителей, первый из которых – число 16, а каждый следующий на 1 меньше предыдущего, т.е. 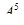 = 16·15·14·13·12=524160.
= 16·15·14·13·12=524160.
В пособии приводятся примеры применения формулы числа размещений.
Пример 1. Учащиеся второго класса изучают 8 предметов. Сколькими способами можно составить расписание на один день, чтобы в нем было четыре различных предмета?
Любое расписание на один день, составленное из 4 различных предметов, отличается от другого либо предметами, либо порядком следования предметов. Значит, в этом примере идет речь о размещениях из 8 элементов по 4. Имеем, 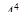 = 8·7·6·5 = 1684.
= 8·7·6·5 = 1684.
Расписание можно составить 1680 способами.
Пример 2. Сколько трехзначных чисел (без повторения цифр) можно составить из цифр 0, 1, 2, 3, 4, 5, 6?
Если среди семи цифр нет нуля, то трехзначных чисел (без повторения), которые можно составить из этих цифр, равно числу размещений из 7 элементов по 3. однако среди данных цифр есть цифра 0, с которой не может начинаться трехзначное число. Поэтому из размещений из 7 элементов по 3 надо исключить те элементы, у которых первой цифрой является 0. их число равно числу размещений из 6 элементов по 2. значит, искомое число трехзначных чисел равно 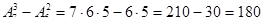 .
.
Из данных цифр можно составить 180 трехзначных чисел (без повторения цифр).
Упражнения
54. Сколькими способами может разместиться семья из трех человек в четырехместном купе, если других пассажиров в купе нет?
55. Из 30 участников собрания надо выбрать председателя и секретаря. Сколькими способами это можно сделать?
56. Сколькими способами могут занять первое, второе и третье места 8 участниц финального забега на дистанцию 100 м?
57. На станции 7 запасных путей. Сколькими способами можно расставить на них 4 поезда?
58. Сколькими способами можно изготовить трехцветный флаг с горизонтальными полосами, если имеется материал 7 различных цветов?
59. На соревнования по легкой атлетике приехала команда из 12 спортсменок. Сколькими способами тренер может определить, кто из них побежит в эстафете 4×100 м на первом, втором, третьем и четвертом этапах?
Решение. В этом задании идет речь о размещениях из 12 элементов по 4. Таким образом, искомое число выбора спортсменок равно 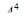 = 12·11·10·9 = 11880 способов.
= 12·11·10·9 = 11880 способов.
60. Сколькими способами могут быть распределены первая, вторая и третья премии между 15 участниками конкурса?
61. Сколькими способами 6 студентов, сдающих экзамен, могут занять места в аудитории, в которой стоит 20 одноместных столов?
62. На странице альбома 6 свободных мест для фотографий. Сколькими способами можно вложить в свободные места:
а) 2 фотографии; б) 4 фотографии; в) 6 фотографий?
63. На плоскости отметили 5 точек. Их надо обозначить латинскими буквами. Сколькими способами это можно сделать (в латинском алфавите 26 букв)?
64. Сколько четырехзначных чисел, в которых нет одинаковых цифр, можно составить из цифр:
а) 1, 3, 5, 7, 9; б) 0, 2, 4, 6, 8?
65. Из трехзначных чисел, записанных с помощью цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 (без повторения цифр), сколько таких, в которых:
а) не встречаются цифры 6 и 7;
б) цифра 8 является последней?
66. Сколько существует семизначных телефонных номеров, в каждом из которых все цифры различные и первая цифра отлична от нуля?
Решение. В этом задании идет речь о размещениях из 10 элементов по 7, т.е. 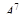 . Но первая цифра номера должна отличаться от нуля, т.е. размещение из 9 элементов по 6.
. Но первая цифра номера должна отличаться от нуля, т.е. размещение из 9 элементов по 6.
Так как из всех размещений надо исключить те, которые начинаются с цифры 0, то имеем: 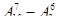 = 10·9·8·7·6·5·4 – 9·8·7·6·5·4 = 604800 – 60480 = 544320.
= 10·9·8·7·6·5·4 – 9·8·7·6·5·4 = 604800 – 60480 = 544320.
67. Сколько различных трехзначных чисел (без повторения цифр) можно составить из цифр 1, 2, 3, 4, 5, таких, которые являются:
а) четными; б) кратными 5?
Сочетания
Пусть имеется пять гвоздик разного цвета. Обозначим их буквами a, b, c, d, е. требуется составить букет из трех гвоздик. Выясним, какие букеты могут быть составлены.
Если в букет входит гвоздика а, то можно составить такие букеты:
abc, abd, abe, acd, ace, ade
Если в букет не входит гвоздика а, но входит гвоздика b, то можно получить такие букеты:
bcd, bce, bde.
Наконец, если в букет не входит ни гвоздика а, ни гвоздика b, то возможен только один вариант составления букета: cde.
Мы указали все возможные способы составления букетов, в которых по-разному сочетаются три гвоздики из данных пяти. Говорят, что мы составили все возможные сочетания из пяти элементов по три.
Сочетанием из п элементов по k (0<k<n) называется любое множество, составленное из k элементов, выбранных из данных п элементов.
Число сочетаний из п элементов по k обозначают 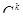 (читают «С из n по k»).
(читают «С из n по k»).
В отличие от размещений в сочетаниях не имеет значения, в каком порядке указаны элементы. Два сочетания из n элементов по k отличаются друг от друга хотя бы одним элементом.
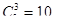 В рассмотренном примере, составив все сочетания из 5 элементов по 3, мы нашли, что
В рассмотренном примере, составив все сочетания из 5 элементов по 3, мы нашли, что 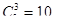
Выведем формулу числа сочетаний из п элементов по k, где k≤n. Для этого сначала выясним, как 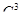 выражается через
выражается через 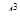 и
и 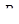 .
.
Мы нашли, что из пяти элементов a, b, c, d, e можно составить следующие сочетания по трем элементам:
abc, abd, abe, acd, ace, ade, bed, bec, bde, cde.
В каждом сочетании выполним все перестановки. Число таких перестановок равно Р3. В результате получим все возможные комбинации из 5 элементов по 5, которые отличаются либо самими элементами, либо порядком элементов, т.е. все размещения из 5 элементов по 3. всего мы получим 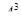 размещений.
размещений.
Значит, 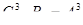 . Отсюда
. Отсюда 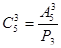 .
.
Аналогично будем рассуждать и в общем случае. Допустим, сто имеется множество, содержащее n элементов, и из его элементов составлены все возможные сочетания по k элементов. Число таких сочетаний равно 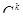 . В каждом сочетании можно выполнить Pk перестановок. В результате мы получим все размещения, которые можно составить из n элементов по k. Их число равно
. В каждом сочетании можно выполнить Pk перестановок. В результате мы получим все размещения, которые можно составить из n элементов по k. Их число равно 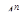 .
.
Значит, 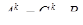 . Отсюда,
. Отсюда, 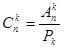 .
.
Мы получили формулу: 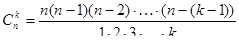 .
.
Формулу числа сочетаний можно записать в другом виде. Умножим числитель и знаменатель дроби на (n – k)!, где n ¹ k. Получим:
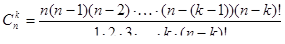
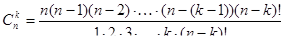
Очевидно, что в числителе дроби записано произведение всех натуральных чисел от n до 1, взятых в порядке убывания, т.е. числитель дроби равен п!.
Получаем формулу: 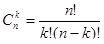 .
.
Заметим, что эту формулу можно использовать и в случае, когда n=k, если принять по определению, что 0!=1.
Пример 1. Из 15 членов туристической группы надо выбрать трех дежурных. Сколькими способами можно сделать этот выбор?
Каждый выбор отличается от другого хотя бы одним дежурным. Значит, здесь речь идет о сочетаниях из 15 элементов по 3:
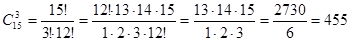 .
.
Следовательно, трех дежурных можно выбрать 455 способами.
Пример 2. Из вазы с фруктами, в которой лежит 9 яблок и 6 груш, надо выбрать 3 яблока и 2 груши. Сколькими способами можно сделать такой выбор?
Выбрать 3 яблока из 9 можно 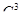 способами, а выбрать 2 груши из 6 можно
способами, а выбрать 2 груши из 6 можно 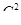 способами. Так как при каждом выборе яблок груши можно выбрать
способами. Так как при каждом выборе яблок груши можно выбрать 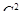 способами, то сделать выбор фруктов, о котором говорится в задаче, можно
способами, то сделать выбор фруктов, о котором говорится в задаче, можно 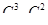 способами.
способами.
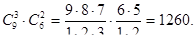
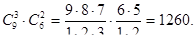
Значит, указанный выбор фруктов можно сделать 1260 способами.
Упражнения
68. В классе 7 человек успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для участия в математической олимпиаде?
69. В магазине «Филателия» продается 8 различных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора?
Решение. Искомое число способа выбора трех наборов равно 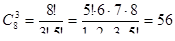 .
.
70. Учащимся дали список из 10 книг, которые рекомендуется прочитать во время каникул. Сколькими способами ученик может выбрать из них 6 книг?
71. Из трех игроков, заявленных на теннисный матч, надо выбрать двух для выступления в парном разряде (порядок игроков не важен). Сколькими способами это можно сделать?
72. Сколькими способами можно выбрать 49 предметов из 50
73. Сколькими способами можно отобрать стартовую шестерку в волейбольном матче, если в команде заявлено 10 игроков?
74. Из лаборатории, в которой работают заведующий и 10 сотрудников, надо отправить 5 человек в командировку. Сколькими способами это можно сделать, если:
а) заведующий лабораторией должен ехать в командировку;
б) заведующий лабораторией должен остаться?
75. На полке стоит 12 книг: англо-русский словарь и 11 художественных произведений на английском языке. Сколькими способами читатель может выбрать 3 книги, если:
а) словарь нужен ему обязательно; б) словарь ему не нужен?
Решение. а) Так как выбор англо-русского словаря уже сделан, то оставшиеся 2 книги из 11 можно выбрать 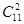 способами. Следовательно,
способами. Следовательно, 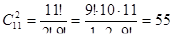 .
.
Значит, выбор можно сделать 55 способами.
б) В этом случае надо выбрать 3 книги из 11. это можно сделать 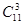 способами. Находим, что
способами. Находим, что 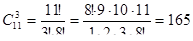 .
.
Выбор можно сделать 165 способами.
Ответ: а) 55 способов;
б) 165 способов.
76. В классе учатся 16 мальчиков и 12 девочек. Для уборки территории требуется выделить 4 мальчиков и 3 девочек. Сколькими способами это можно сделать?
Решение. Четырех мальчиков из 16 можно выделить 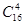 способами, а трех девочек из 12 можно выделить
способами, а трех девочек из 12 можно выделить 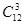 способами. Каждому выбору четырех мальчиков соответствует
способами. Каждому выбору четырех мальчиков соответствует 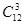 возможностей выбора трех девочек. Значит, указанный выбор дежурных можно сделать
возможностей выбора трех девочек. Значит, указанный выбор дежурных можно сделать 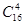 ×
× 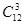 способами.
способами.
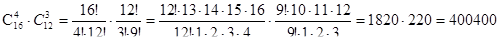 .
.
Значит, выбор дежурных можно сделать 400400 способами.
Ответ: 400400 способов.
В задачах 54-60 рассматриваются различные комбинации элементов (перестановки, размещения, сочетания).
77. Сколько среди всех перестановок букв слова «высота» таких, которые:
а) начинаются с буквы в;
б) начинаются с буквы а, а оканчиваются буквой т?
78. Пять мальчиков и четыре девочки хотят сесть на девятиместную скамейку так, чтобы каждая девочка сидела между двумя мальчиками. Сколькими способами они могут это сделать?
79. Из 12 солдат, в число которых входят Иванов и Петров, надо отправить в наряд 3 человек. Сколькими способами это можно сделать, если:
а) Иванов и Петров должны пойти в наряд;
б) Иванов и петров должны остаться;
в) Иванов должен пойти, а Петров – остаться?
80. В шахматном кружке занимаются 16 человек. Сколькими способами тренер может выбрать из них для предстоящего турнира:
а) команду из четырех человек;
б) команду из четырех человек, указав при этом, кто из членов команды будет играть на первой, второй, третьей и четвертой досках?
81. Для ремонта школы прибыла бригада, состоящая из 12 человек. Тре
|
из
5.00
|
Обсуждение в статье: Сборник основных правил комбинаторики и упражнений для их применения |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

