 |
Главная |
Оператор интегрирования
|
из
5.00
|
Рассмотрим оператор интегрирования, действующий в пространстве непрерывных функций - C[a,b], определенных на отрезке [a,b], заданный следующим образом:
Аf(t) = 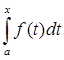 .
.
f(t) – функция, непрерывная на [a, b],t 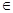 [a,x]; x
[a,x]; x 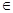 [a,b]; a,b
[a,b]; a,b 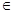 R;
R;
Поскольку 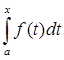 - интеграл с переменным верхним пределом, есть функция от верхнего предела – F(x), a
- интеграл с переменным верхним пределом, есть функция от верхнего предела – F(x), a 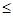 x
x 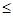 b; Следовательно можно утверждать, что А – оператор.
b; Следовательно можно утверждать, что А – оператор.
Проверим оператор A на линейность. По определению 1:
1) Аксиома аддитивности: A(f+g) = A(f) + A(g).
A(f+g) = 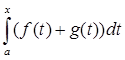 =
= 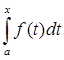 +
+ 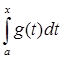 = A(f) + A(g).
= A(f) + A(g).
2) Аксиома однородности: A(kf) = kA(f).
A(kf) = 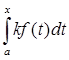 = k*
= k* 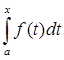 = kA(f).
= kA(f).
Исходя из свойств интеграла:
1. интеграл от суммы, есть сумма интегралов;
2. вынесение const за знак интеграла.
Можно сделать вывод: оператор А является линейным.
3) Проверим, является ли А непрерывным, для этого воспользуемся определением непрерывности:
p (fn(t), f0(t)) 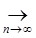 0
0 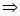 p (A fn(t), Af0(t))
p (A fn(t), Af0(t)) 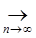 0.
0.
Оператор А, действует в пространстве C[a,b], в котором расстояние между функциями определяется следующим образом:
p (fn(t), f0(t)) = 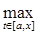 | fn(t) - f0(t)|.
| fn(t) - f0(t)|.
Решение:
p (A fn(t), Af0(t)) = 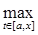 |
| 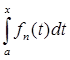 -
- 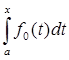 |.
|.
| 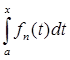 -
- 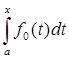 | = |
| = | 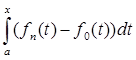 |
| 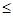
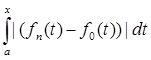
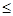
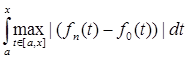 = p (fn(t), f0(t))
= p (fn(t), f0(t)) 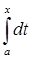 = p (fn(t), f0(t)) (x-a)
= p (fn(t), f0(t)) (x-a) 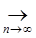 0
0
a 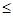 x
x 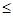 b.
b.
Таким образом p (A fn(t), Af0(t)) 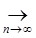 0. следовательно по определению 2 оператор А непрерывен.
0. следовательно по определению 2 оператор А непрерывен.
4) Непрерывный оператор является ограниченным (теорема 3):
| 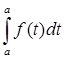 |
| 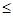 |
| 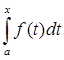 |
| 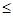 |
| 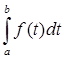 |
|
| 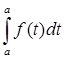 | = 0; |
| = 0; | 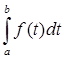 | = |b-a|.
| = |b-a|.
0 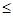 |
| 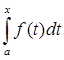 |
| 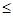 |b-a|.
|b-a|.
5) Оператор А ограниченный, следовательно у него можно найти норму. Найдем норму оператора А (используя определение ||A||= 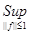 |A(f)|):
|A(f)|):
||A|| = 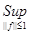 |A(f)| =
|A(f)| = 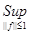 |
| 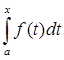 |
| 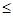
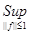
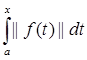
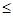
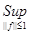
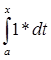 = (x-a);
= (x-a);
a 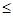 x
x 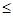 b;
b;
Норма оператора А: ||A|| = (b-a);
6) Обратимость интегрального оператора и его спектр.
Возьмем пространство S = {f 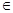 C[0,b] / f(0) = 0} с нормой ||f|| =
C[0,b] / f(0) = 0} с нормой ||f|| = 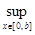 |f(x)|.
|f(x)|.
В пространстве S рассмотрим оператор А:
Аf = 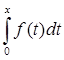
x 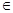 [0,b], t
[0,b], t 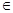 [0,x];
[0,x];
Найдем оператор обратный к (A - 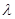 *I),
*I), 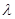
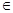 R;
R;
(A - 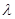 *I)*f = g
*I)*f = g
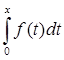 -
- 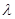 *f(x) = g(x) (1)
*f(x) = g(x) (1)
Пусть функции f и g дифференцируемы;
Продифференцируем уравнение (1), получим:
f - 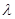 *f/ = g/ (2)
*f/ = g/ (2)
Это уравнение (2) – дифференциальное неоднородное линейное уравнение. Решим это уравнение, используя метод Бернулли.
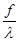 - f/ =
- f/ = 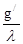
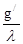 -
- 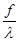 + f/ = 0 (3)
+ f/ = 0 (3)
Представим решение уравнения в виде: f(x) = U(x)*V(x), тогда уравнение (3) примет вид:
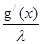 -
- 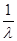 *U*V + U/ *V + U*V/ = 0
*U*V + U/ *V + U*V/ = 0
U/ *V + U*V/ - 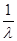 *U*V = -
*U*V = - 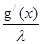
U/ *V + U*(V/ - 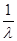 *V) = -
*V) = - 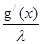 (4)
(4)
Решаем однородное линейное уравнение:
V/ - 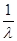 *V = 0
*V = 0
V/ = 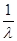 *V
*V
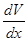 =
= 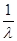 *V
*V
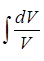 =
= 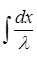
LnV = 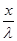 + c
+ c
V = 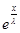 *
* 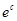 , пусть
, пусть 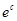 = с1
= с1
V = с1* 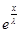
Подставим частное решение однородного уравнения в уравнение (4) при условии, что V/ - 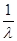 *V = 0.
*V = 0.
Получим уравнение:
U/ * с1* 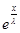 = -
= - 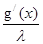
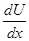 = -
= - 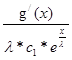
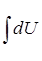 = -
= - 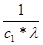 *
* 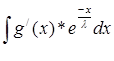
U = - 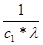 *
* 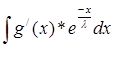
Подставим U и V в f(x) = U(x)*V(x) и получим:
f(x) = с1* 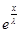 *(-
*(- 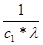 )*
)* 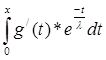
найдем интеграл Y = 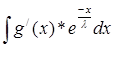 , интегрируем по частям:
, интегрируем по частям:
dz = g/(x)dx;
z = 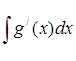 = g(x);
= g(x);
j = 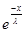 ;
;
dj = - 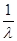 *
* 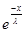 dx;
dx;
Y = g(x)* 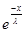 +
+ 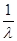 *
* 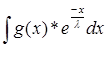
Подставим полученное значение в выражение f(x), которое примет вид:
f(x) = - 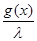 -
- 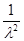 *
* 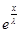 *
* 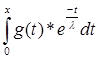 ;
;
Получим оператор В:
Bg = - 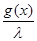 -
- 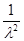 *
* 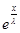 *
* 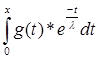 ;
;
x 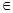 [0,b], t
[0,b], t 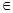 [0,x], g(x)
[0,x], g(x) 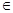 S,
S, 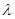 - произвольное число.
- произвольное число.
Оператор В не существует, если 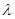 = 0;
= 0;
Рассмотрим ограниченность оператора В для всех 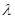
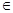 R,
R, 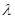
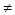 0;
0;
||Bg|| = ||f(x)|| = 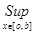 |f(x)| =
|f(x)| = 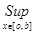 |-
|- 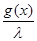 -
- 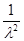 *
* 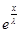 *
* 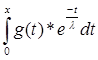 |
| 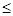
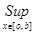 (|
(| 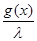 | + |
| + | 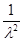 *
* 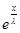 *
* 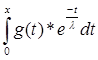 |)
|) 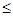
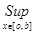 |
| 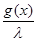 | +
| + 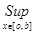 |
| 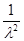 *
* 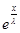 *
* 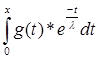 |
| 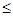
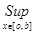 |
| 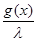 | +
| + 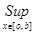 |
| 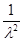 *
* 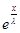 |*
|* 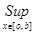 |g(x)*
|g(x)* 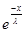 |*|x|
|*|x| 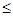
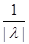 *
* 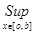 |g(x)| +
|g(x)| + 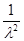
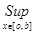
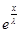 *
* 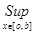 |g(x)|*
|g(x)|* 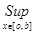 (|
(| 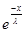 |*|x|)
|*|x|) 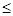
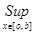 |g(x)|*(
|g(x)|*( 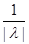 +
+ 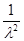 *
* 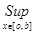
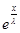 *
* 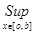
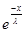 *b);
*b);
При 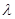 > 0
> 0
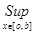
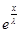 =
= 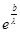 ;
;
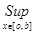
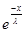 = 1;
= 1;
При 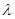 < 0
< 0
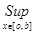
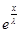 =1;
=1;
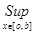
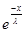 =
= 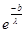 ;
;
Эти оба случая можно записать в общем виде: 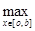 {1,
{1, 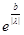 }, тогда
}, тогда
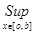 |g(x)|*(
|g(x)|*( 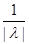 +
+ 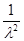 *
* 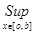
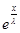 *
* 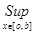
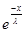 *b)
*b) 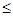
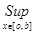 |g(x)|*(
|g(x)|*( 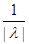 +
+ 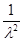 *
* 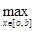 {1,
{1, 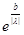 }*b) = ||g(x)||*(
}*b) = ||g(x)||*( 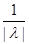 +
+ 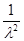 *
* 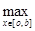 {1,
{1, 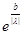 }*b);
}*b);
Итак:
||Bg|| 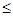 ||g(x)||*(
||g(x)||*( 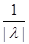 +
+ 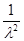 *
* 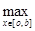 {1,
{1, 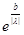 }*b);
}*b);
То есть В – ограничен.
Осталось проверить, что В – оператор, обратный к (A - 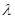 *I).
*I).
Если это так, то произведение этих операторов равно единичному оператору или же (A - 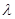 *I)*(Bg) = g(x).
*I)*(Bg) = g(x).
Итак, нужно доказать, что
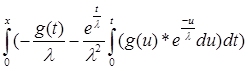 + g(x) +
+ g(x) + 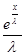 *
* 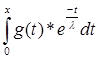 = g(x)
= g(x)
или
- 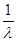 *
* 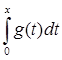 -
- 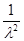
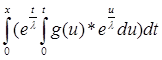 +
+ 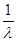 *
* 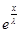 *
* 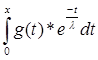 = 0; (*)
= 0; (*)
Возьмем производную от левой части (*) и получим:
- 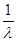 *g(x) -
*g(x) - 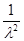 *
* 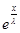 *
* 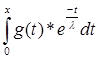 +
+ 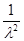 *
* 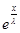 *
* 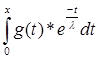 +
+ 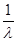 *
* 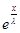 *
* 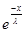 * g(x) = -
* g(x) = - 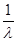 *g(x) +
*g(x) + 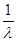 *g(x) -
*g(x) - 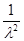 *
* 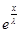 *
* 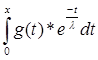 +
+ 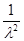 *
* 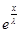 *
* 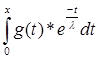 = 0;
= 0;
Следовательно, выражение (*) = const. Но, так как при x=0 выражение (*) (точнее его левая часть) равно 0, то и const=0. Значит В – обратный оператор к (A - 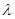 *I) в S.
*I) в S.
Итак, мы получили ограниченный оператор В, обратный к (A - 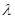 *I), который существует при
*I), который существует при 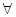
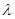
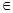 R, за исключением
R, за исключением 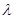 =0, то есть все возможные
=0, то есть все возможные 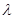
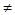 0 – это регулярные точки оператора А; Сам же оператор В – резольвента оператора А. Спектр оператора А – значение
0 – это регулярные точки оператора А; Сам же оператор В – резольвента оператора А. Спектр оператора А – значение 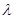 при которых В не существует, то есть
при которых В не существует, то есть 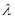 =0.
=0.
Вывод:
Оператор интегрирования, действующий в пространстве непрерывных функций – C[a,b], определенных на отрезке [a,b], заданный следующим образом: Аf(t) = 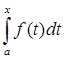 , где f(t) – функция, непрерывная на [a, b], t
, где f(t) – функция, непрерывная на [a, b], t 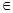 [a,x]; x
[a,x]; x 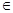 [a,b]; a,b
[a,b]; a,b 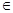 R:
R:
1. линейный;
2. непрерывный;
3. ограниченный: 0 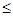 |
| 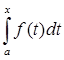 |
| 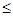 |b-a|;
|b-a|;
4. норма A: ||A|| = (b-a);
5. резольвента оператора А: R 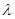 (A) = -
(A) = - 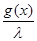 -
- 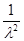 *
* 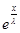 *
* 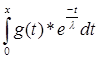 , где
, где
x 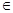 [0,b], t
[0,b], t 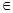 [0,x], g(x)
[0,x], g(x) 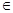 S, S = {f
S, S = {f 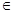 C[0,b] / f(0) = 0} с нормой ||f||=
C[0,b] / f(0) = 0} с нормой ||f||= 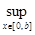 |f(x)|, g(x) =
|f(x)|, g(x) = 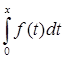 -
- 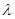 *f(x),
*f(x), 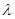 - произвольное число.
- произвольное число.
6. Спектр оператора А: 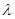 =0.
=0.
|
из
5.00
|
Обсуждение в статье: Оператор интегрирования |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

