Глава 2. Реализация сингулярного разложения

2019-12-29

227

Обсуждений (0)

0.00 из 5.00 0 оценок

1 234 5 6

Алгоритмы

QR–алгоритм начинается с разложения матрицы по Грамму-Шмидту 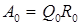, затем меняются местами сомножители: 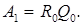Эта матрица подобна первоначальной, 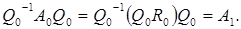Этот процесс продолжается, причем собственные значения не изменяются:

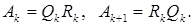
Эта формула описывает QR–алгоритм без сдвигов. Обычно время которое тратится на такой процесс пропорционально кубу размерности матрицы – n³. Необходимо процесс ускорить, для чего используется предварительное приведение матрицы А к форме Хессенберга[8] а также используется алгоритм со сдвигом. Форма Хессенберга представляет из себя верхнюю треугольную матрицу (верхняя форма Хессенберга) у которой сохранена одна диагональ ниже главной, а элементы ниже этой диагонали равны нулю. Если матрица симметрична, то легко видеть, что матрица Хессенберга превращается в трехдиагональную матрицу[9]. При использовании матрицы Хессенберга время процесса пропорционально n², а при использовании трехдиагональной матрицы – n.

Можно использовать другие соотношения

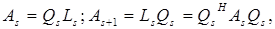
где Q_s – унитарная, а L_s – нижняя треугольная матрица. Такой алгоритм носит название QL–алгоритма.

В общем случае, когда все собственные значения матрицы различны, последовательность матриц A_s имеет пределом нижнюю треугольную матрицу 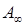, диагональные элементы которой представляют собой собственные значения матрицы А, расположенные в порядке возрастания их модулей. Если матрица А имеет кратные собственные значения, то предельная матрица не является треугольной, а содержит диагональные блоки порядка p, соответствующие собственному числу 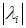кратности p.

В общем случае, наддиагональный элемент 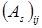матрицы A_s на s-ом шаге асимптотически равен 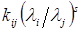, где k_ij – постоянная величина. Сходимость QL–алгоритма вообще говоря недостаточна. Сходимость можно улучшить, если на каждом шаге вместо матрицы A_s использовать матрицу A_s-k_sI (QL–алгоритм со сдвигом). Последовательность вычислений в этом случае описывается следующими соотношениями:

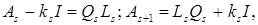
которые определяют матрицу 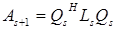. При этом асимптотическое поведение элемента 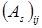определено соотношением 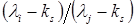, а не 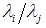, как прежде. Если сдвиг k_s выбрать близко к величине 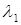(наименьшее собственное значение), то в пределе внедиагональные элементы первой строки будут очень быстро стремиться к нулю. Когда ими можно пренебречь, элемент 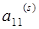с рабочей точностью равен 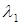, остальные являются собственными значениями оставшейся матрицы n-1-го порядка. Тогда, если QL–алгоритм выполнен без ускорения сходимости, то все равно 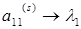, и поэтому автоматически можно выделить величину сдвига k_s.

Если матрица А эрмитова, то очевидно, что и все матрицы А _s эрмитовы; если А действительная и симметричная, то все Q_s ортогональны и все А _s действительны и симметричны.

Реализация разложения

Таким образом, разложение 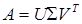производится в два этапа. Сначала матрица А посредством двух конечных последовательностей преобразований Хаусхолдера где , приводится к верхней двухдиагональной форме следующего вида:

Далее реализуется итерационный процесс приведения двухдиагональной матрицы J₀ к диагональной форме, так что имеет место следующая последовательность: 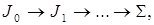где 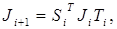а S_i и T_i – диагональные матрицы.

Матрицы T_i выбираются так, чтобы последовательность матриц 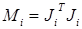сходилась к двухдиагональной матрице. Матрицы же S_i выбирают так, чтобы все J_i сохраняли двухдиагональную форму. Переход 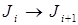осуществляется с помощью плоских вращений (10) – преобразований Гивенса. Отсюда, 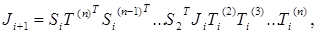где

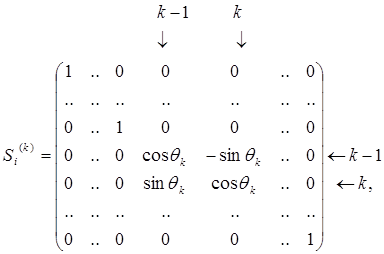
а матрица 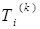вычисляется аналогично с заменой 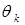на .

Пусть начальный угол 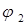произволен, однако следующие значения угла необходимо выбирать так, чтобы матрица J_i₊₁ имела ту же форму, что и J_i. Таким образом 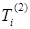не аннулирует ни одного элемента матрицы, но добавляет элемент 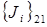; 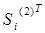аннулирует 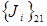но добавляет 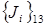; 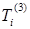аннулирует 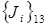но добавляет 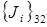и т.д., наконец, 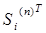аннулирует 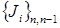и ничего не добавляет.

Этот процесс часто называют процессом преследования. Так как 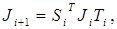, то 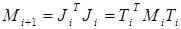, и M_i₊₁ – трехдиагональная матрица, точно так же, как и M_i. Начальный угол 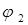можно выбрать так, чтобы преобразование 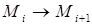было QR–преобразованием со сдвигом, равным s.

Обычный QR–алгоритм со сдвигом можно записать в следующем виде:

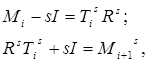
где 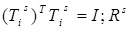– верхняя треугольная матрица. Следовательно, 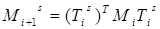. Параметр сдвига s определяется собственным значением нижнего минора (размерности 2´2) матрицы M_i. При таком выборе параметра s метод обладает глобальной и почти всегда кубичной сходимостью.

2019-12-29

227

Обсуждений (0)

0.00 из 5.00 0 оценок

1 234 5 6

Обсуждение в статье: Глава 2. Реализация сингулярного разложения

Обсуждений еще не было, будьте первым... ↓↓↓