 |
Главная |
Перечень условных обозначений
|
из
5.00
|
Оглавление
Введение
Перечень условных обозначений
Основные понятия
Изометрии
Проективные преобразования
Структурные теоремы. Порядки симплектических групп
Центры
Коммутанты
Теоремы о простоте
Основные результаты
Заключение
Список использованных источников
Введение
Говорят, что конечная группа  допускает факторизацию, если
допускает факторизацию, если  для некоторых подгрупп
для некоторых подгрупп  и
и  группы
группы  . При этом возникают две задачи: какие факторизации допускает заданная группа
. При этом возникают две задачи: какие факторизации допускает заданная группа  и как строение сомножителей
и как строение сомножителей  и
и  влияет на строение самой группы
влияет на строение самой группы  . Естественно, что изучение конечных групп, обладающих факторизацией, дает возможность глубже понять строение конечной группы. Данная тематика изучалась такими видными математиками как Ф. Холл, С.А. Чунихин, Х. Виландт, Л.С. Казарин, Д.И. Зайцев, С.А. Сыскин и др. Ими был доказан ряд глубоких результатов в теории конечных групп. Аналогичные задачи возникают и в других разделах математики (например, в алгебрах Ли).
. Естественно, что изучение конечных групп, обладающих факторизацией, дает возможность глубже понять строение конечной группы. Данная тематика изучалась такими видными математиками как Ф. Холл, С.А. Чунихин, Х. Виландт, Л.С. Казарин, Д.И. Зайцев, С.А. Сыскин и др. Ими был доказан ряд глубоких результатов в теории конечных групп. Аналогичные задачи возникают и в других разделах математики (например, в алгебрах Ли).
После завершения классификации конечных простых неабелевых групп актуальной стала задача получения факторизаций конкретных простых неабелевых групп и, в частности, простых групп лиевского типа малого лиевского ранга. Данные вопросы рассматривались Н. Ито, который получил все факторизации линейных групп лиевского ранга 1 над конечным полем Галуа, а также С. Блаумом, описавшим факторизации линейных и унитарных групп размерности 3.
В дипломной работе рассмотрены факторизации четырехмерных симплектических групп. Для таких групп найдены все максимальные факторизации.
Перечень условных обозначений
В работе все рассматриваемые группы предполагаются конечными. Буквами  обозначаются простые числа.
обозначаются простые числа.
Будем различать знак включения множеств  и знак строгого включения
и знак строгого включения  ;
;
 и
и  - соответственно знаки пересечения и объединения множеств;
- соответственно знаки пересечения и объединения множеств;
 - мощность множества
- мощность множества 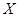 ;
;
 - пустое множество;
- пустое множество;
 - множество всех простых чисел;
- множество всех простых чисел;
 - некоторое множество простых чисел, т.е.
- некоторое множество простых чисел, т.е.  ;
;
 - дополнение к
- дополнение к  во множестве всех простых чисел; в частности,
во множестве всех простых чисел; в частности,  ;
;
Пусть  - группа. Тогда:
- группа. Тогда:
 - порядок группы
- порядок группы  ;
;
 - порядок элемента
- порядок элемента 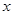 группы
группы  ;
;
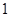 - единичный элемент и единичная подгруппа группы
- единичный элемент и единичная подгруппа группы  ;
;
 - множество всех простых делителей порядка группы
- множество всех простых делителей порядка группы  ;
;
 - множество всех различных простых делителей натурального числа
- множество всех различных простых делителей натурального числа  ;
;
 -группа - группа
-группа - группа  , для которой
, для которой  ;
;
 -группа - группа
-группа - группа  , для которой
, для которой  ;
;
 - подгруппа Фраттини группы
- подгруппа Фраттини группы  , т.е. пересечение всех максимальных подгрупп
, т.е. пересечение всех максимальных подгрупп  ;
;
 - наибольшая нормальная разрешимая подгруппа группы
- наибольшая нормальная разрешимая подгруппа группы  ;
;
 - наибольшая нормальная
- наибольшая нормальная  --подгруппа группы
--подгруппа группы  ;
;
 - наибольшая нормальная
- наибольшая нормальная  --подгруппа группы
--подгруппа группы  ;
;
 -
-  --холловская подгруппа группы
--холловская подгруппа группы  ;
;
 - силовская
- силовская  --подгруппа группы
--подгруппа группы  ;
;
 - дополнение к силовской
- дополнение к силовской  --подгруппе в группе
--подгруппе в группе  , т.е.
, т.е. 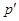 --холловская подгруппа группы
--холловская подгруппа группы  ;
;
 -
-  является подгруппой группы
является подгруппой группы  ;
;
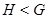 -
-  является собственной подгруппой группы
является собственной подгруппой группы  ;
;
 -
-  является максимальной подгруппой группы
является максимальной подгруппой группы  ;
;
 -
-  является нормальной подгруппой группы
является нормальной подгруппой группы  ;
;
 -
-  является минимальной нормальной подгруппой группы
является минимальной нормальной подгруппой группы  ;
;
 - индекс подгруппы
- индекс подгруппы  в группе
в группе  ;
;
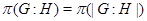 ;
;
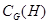 - централизатор подгруппы
- централизатор подгруппы  в группе
в группе  ;
;
 - нормализатор подгруппы
- нормализатор подгруппы  в группе
в группе  ;
;
 - центр группы
- центр группы  ;
;
 - циклическая группа порядка
- циклическая группа порядка  ;
;
Если  , то
, то 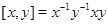 .
.
Если  ,
,  , то
, то  .
.
Классы групп, т.е. совокупности групп, замкнутые относительно изоморфизмов, обозначаются прописными готическими буквами. За некоторыми классами закреплены стандартные обозначения:
 - класс всех сверхразрешимых групп;
- класс всех сверхразрешимых групп;
 - класс всех разрешимых групп.
- класс всех разрешимых групп.
Основные понятия
Группой называется непустое множество  с бинарной алгебраической операцией (умножением), которая удовлетворяет следующим требованием:
с бинарной алгебраической операцией (умножением), которая удовлетворяет следующим требованием:
1) операция определена на  , т.е.
, т.е.  для всех
для всех  ;
;
2) операция ассоциативна, т.е.  для любых
для любых  ;
;
3) в  существует единичный элемент , т.е. такой элемент
существует единичный элемент , т.е. такой элемент  , что
, что  для всех
для всех  , что
, что  для всех
для всех  ;
;
4) каждый элемент обладает обратным, т.е. для любого  существует такой элемент
существует такой элемент  , что
, что 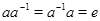 .
.
Более кратко: полугруппа с единицей, в которой каждый элемент обладает обратным, называется группой.
Группу с коммутативной операцией называют коммутативной или абелевой. Если  - конечное множество, являющиеся группой, то
- конечное множество, являющиеся группой, то  называют конечной группой, а число
называют конечной группой, а число  элементов в
элементов в  - порядком группы
- порядком группы  .
.
Подмножество  группы
группы  называется подгруппой, если
называется подгруппой, если 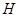 - группа относительно той же операции, которая определена на
- группа относительно той же операции, которая определена на  . Запись
. Запись 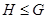 означает, что
означает, что  - подгруппа группы
- подгруппа группы  , а
, а 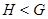 - что
- что  - собственная подгруппа группы
- собственная подгруппа группы  , т.е.
, т.е.  и
и  .
.
Теорема Непустое подмножество  группы
группы  будет подгруппой тогда и только тогда, когда
будет подгруппой тогда и только тогда, когда 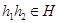 и
и  для всех
для всех  .
.
Пусть  - непустое подмножество группы
- непустое подмножество группы  . Совокупность всех элементов группы
. Совокупность всех элементов группы  , перестановочных с каждым элементом множества
, перестановочных с каждым элементом множества  , называется централизатором множества
, называется централизатором множества  в группе
в группе  и обозначается через
и обозначается через  .
.
Лемма 1. Если  - подмножество группы
- подмножество группы  , то централизатор
, то централизатор  является подгруппой.
является подгруппой.
2. Если  и
и  - подмножество группы
- подмножество группы  и
и  , то
, то 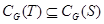 .
.
3. Если  - подмножество группы
- подмножество группы  и
и  , то
, то  .
.
Центром группы  называется совокупность всех элементов из
называется совокупность всех элементов из  , перестановочных с каждым элементом группы. Центр обозначается через
, перестановочных с каждым элементом группы. Центр обозначается через  . Ясно, что
. Ясно, что  , т.е. центр группы
, т.е. центр группы  совпадает с централизатором подмножества
совпадает с централизатором подмножества  в группе
в группе  . Кроме того,
. Кроме того,  .
.
Зафиксируем в группе  элемент
элемент  . Пересечение всех подгрупп группы
. Пересечение всех подгрупп группы  , содержащих элемент
, содержащих элемент  , назовем циклической подгруппой, порожденной элементом
, назовем циклической подгруппой, порожденной элементом  , и обозначим через
, и обозначим через  .
.
Теорема Циклическая подгрупппа  , порожденная элементом
, порожденная элементом  , состоит из всевозможных целых степеней элемента
, состоит из всевозможных целых степеней элемента  , т.е.
, т.е.  .
.
Следствие Циклическая подгруппа абелева.
Пусть  - элемент группы
- элемент группы  . Если все степени элемента
. Если все степени элемента  различны, т.е.
различны, т.е.  для всех целых
для всех целых  , то говорят, что элемента
, то говорят, что элемента  имеет бесконечный порядок.
имеет бесконечный порядок.
Если  - непустое подмножество группы
- непустое подмножество группы  и
и 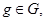 то
то 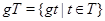 и
и  . Элемент
. Элемент  называется перестановочным с подмножеством
называется перестановочным с подмножеством  , если
, если  . Равенство
. Равенство  означает, что для любого элемента
означает, что для любого элемента 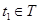 существует такой элемент
существует такой элемент 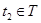 , что
, что  . Если элемент
. Если элемент 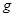 перестановочен с подмножеством
перестановочен с подмножеством  , то
, то  и
и  . Совокупность всех элементов группы
. Совокупность всех элементов группы  , перестановочных с подмножеством
, перестановочных с подмножеством  , называется нормализатором подмножества
, называется нормализатором подмножества  в группе
в группе  и обозначается через
и обозначается через  . Итак,
. Итак,

Лемма Пусть  - непустое подмножество группы
- непустое подмножество группы  ,
, 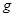 - произвольный элемент группы
- произвольный элемент группы  . Тогда:
. Тогда:
1)  ;
;
2)  ;
;
3)  ;
;
4)  ;
;
5) если  - подгруппа группы
- подгруппа группы  , то
, то  .
.
Подгруппа  называется нормальной подгруппой группы
называется нормальной подгруппой группы  , если
, если  для всех
для всех  . Запись
. Запись  читается: "
читается: "  - нормальная подгруппа группы
- нормальная подгруппа группы  ". Равенство
". Равенство  означает, что для любого элемента
означает, что для любого элемента  существует элемент
существует элемент  такой, что
такой, что  .
.
Теорема Для подгруппы  группы
группы  следующие утверждения эквивалентны:
следующие утверждения эквивалентны:
1)  - нормальная подгруппа;
- нормальная подгруппа;
2) подгруппа  вместе с каждым своим элементом содержит все ему сопряженные элементы, т.е.
вместе с каждым своим элементом содержит все ему сопряженные элементы, т.е.  для всех
для всех  ;
;
3) подгруппа  совпадает с каждой своей сопряженной подгруппой, т.е.
совпадает с каждой своей сопряженной подгруппой, т.е.  для всех
для всех  .
.
Лемма Пусть  - подгруппа группы
- подгруппа группы  . Тогда:
. Тогда:
1)  ;
;
2) если 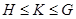 и
и 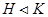 , то
, то  ;
;
3) 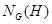 - наибольшая подгруппа группы
- наибольшая подгруппа группы  , в которой
, в которой  нормальна;
нормальна;
4) если  , то
, то  . Обратно, если
. Обратно, если  , то
, то  ;
;
5) 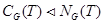 для любого непустого подмножества
для любого непустого подмножества  группы
группы  .
.
В каждой группе  тривиальные подгруппы (единичная подгруппа
тривиальные подгруппы (единичная подгруппа  и сама группа
и сама группа  ) являются нормальными подгруппами. Если в неединичной группе
) являются нормальными подгруппами. Если в неединичной группе  нет других нормальных подгрупп, то группа
нет других нормальных подгрупп, то группа  называется простой. Единичную группу
называется простой. Единичную группу  считают непростой.
считают непростой.
Изометрии
|
из
5.00
|
Обсуждение в статье: Перечень условных обозначений |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

