 |
Главная |
Проективные преобразования
|
из
5.00
|
Геометрическое преобразование  абстрактного векторного пространства
абстрактного векторного пространства  на абстрактное векторное пространство
на абстрактное векторное пространство  - это биекция
- это биекция  со следующим свойством: подмножество
со следующим свойством: подмножество  пространства
пространства 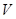 тогда и только тогда является подпространством в
тогда и только тогда является подпространством в 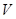 , когда
, когда  - подпространство в
- подпространство в 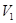 .
.
Очевидно, что композиция геометрических преобразований - геометрическое преобразование и преобразование, обратное к геометрическому, - также геометрическое. Геометрическое преобразование сохраняет включение, объединение и пересечение подпространств, а также ряды Жордана -- Гёльдера, поэтому справедливо следующее предложение.
Предложение Если  - геометрическое преобразование пространства
- геометрическое преобразование пространства  на
на 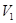 , то для любых подпространств
, то для любых подпространств  ,
,  пространства
пространства 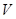 выполняются соотношения
выполняются соотношения
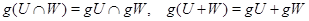
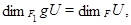

Под проективным пространством 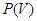 пространства
пространства  мы будем понимать множество всех подпространств пространства
мы будем понимать множество всех подпространств пространства 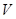 . Таким образом,
. Таким образом,  состоит из элементов множества
состоит из элементов множества 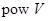 , являющихся подпространствами в
, являющихся подпространствами в  ;
;  - это частично упорядоченное множество, отношение порядка в котором индуцируется теоретико-множественным включением в
- это частично упорядоченное множество, отношение порядка в котором индуцируется теоретико-множественным включением в 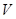 . Любые два элемента
. Любые два элемента  и
и  из
из  имеют объединение и пересечение, а именно
имеют объединение и пересечение, а именно  и
и 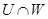 , так что
, так что  - решетка; она имеет наибольший элемент
- решетка; она имеет наибольший элемент 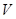 и наименьший элемент
и наименьший элемент  . Каждому элементу
. Каждому элементу  пространства
пространства 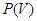 сопоставляется число
сопоставляется число  . Каждое
. Каждое  из
из 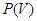 обладает рядом Жордана -- Гёльдера
обладает рядом Жордана -- Гёльдера  , и все такие ряды имеют длину
, и все такие ряды имеют длину  . Положим
. Положим

и назовем  ,
,  ,
, 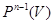 множествами прямых, плоскостей и гиперплоскостей пространства
множествами прямых, плоскостей и гиперплоскостей пространства 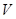 соответственно.
соответственно.
Проективность  пространства
пространства 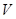 на
на  - это биекция
- это биекция  со следующим свойством: для любых
со следующим свойством: для любых  ,
,  из
из 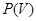 включение
включение  имеет место тогда и только тогда, когда
имеет место тогда и только тогда, когда  .
.
Очевидно, что композиция проективностей - проективность и отображение, обратное к проективности, - также проективность. Проективность пространства  на
на  сохраняет порядок, объединения, пересечения и ряды Жордана -- Гёльдера для элементов пространств
сохраняет порядок, объединения, пересечения и ряды Жордана -- Гёльдера для элементов пространств 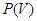 и
и 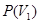 , поэтому справедливо следующее предложение.
, поэтому справедливо следующее предложение.
Предложение Если  - проективность пространства
- проективность пространства  на
на 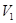 , то для любых элементов
, то для любых элементов  ,
,  из
из 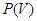 выполняются соотношения
выполняются соотношения
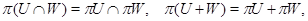

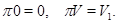
В частности,  отображает
отображает  на
на  и определяется своими значениями на
и определяется своими значениями на  , т. е. на прямых.
, т. е. на прямых.
Если  - геометрическое преобразование, то отображение
- геометрическое преобразование, то отображение 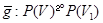 , полученное из
, полученное из  сужением, является проективностью пространства
сужением, является проективностью пространства  на
на  . Всякая проективность
. Всякая проективность  , имеющая вид
, имеющая вид  для некоторого такого
для некоторого такого  , будет называться проективным геометрическим преобразованием пространства
, будет называться проективным геометрическим преобразованием пространства  на
на  . Черту мы будем всегда использовать для обозначения проективного геометрического преобразования
. Черту мы будем всегда использовать для обозначения проективного геометрического преобразования  , полученного описанным способом из геометрического преобразования
, полученного описанным способом из геометрического преобразования  . Таким образом,
. Таким образом,  переводит подпространство
переводит подпространство  пространства
пространства 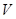 , т.е. точку
, т.е. точку  из
из  , в подпространство
, в подпространство 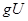 пространства
пространства 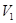 . Имеем
. Имеем

В частности, композиция проективных геометрических преобразований и преобразование, обратное к проективному геометрическому, сами являются проективными геометрическими.
Геометрическое преобразование пространства  есть по определению геометрическое преобразование пространства
есть по определению геометрическое преобразование пространства 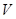 на себя. Множество геометрических преобразований пространства
на себя. Множество геометрических преобразований пространства 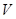 является подгруппой группы подстановок множества
является подгруппой группы подстановок множества 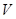 . Она будет обозначаться через
. Она будет обозначаться через  и называться общей геометрической группой пространства
и называться общей геометрической группой пространства 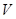 . Под группой геометрических преобразований пространства
. Под группой геометрических преобразований пространства 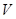 мы будем понимать произвольную подгруппу группы
мы будем понимать произвольную подгруппу группы 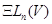 . Общая линейная группа
. Общая линейная группа  и специальная линейная группа
и специальная линейная группа  являются, следовательно, группами геометрических преобразований. Под группой линейных преобразований будем понимать любую подгруппу группы
являются, следовательно, группами геометрических преобразований. Под группой линейных преобразований будем понимать любую подгруппу группы  .
.
Проективность пространства 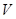 есть по определению проективность этого пространства на себя. Множество проективностей пространства
есть по определению проективность этого пространства на себя. Множество проективностей пространства  - подгруппа группы подстановок множества
- подгруппа группы подстановок множества 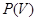 , которую мы будем называть общей группой проективностей пространства
, которую мы будем называть общей группой проективностей пространства 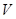 . Применение черты индуцирует гомоморфизм
. Применение черты индуцирует гомоморфизм

Иногда мы будем использовать  вместо
вместо  , полагая
, полагая
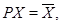
для образа  подмножества
подмножества  из
из  при
при  . В частности,
. В частности,  и
и  - подгруппы группы проективностей пространства
- подгруппы группы проективностей пространства 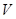 , они называются проективной общей линейной группой и проективной специальной линейной группой пространства
, они называются проективной общей линейной группой и проективной специальной линейной группой пространства 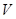 . Было доказано, что
. Было доказано, что 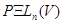 совпадает с группой всех проективностей пространства
совпадает с группой всех проективностей пространства 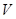 , поэтому мы используем это обозначение для обеих групп. Под группой проективностей пространства
, поэтому мы используем это обозначение для обеих групп. Под группой проективностей пространства 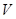 будем понимать любую подгруппу группы
будем понимать любую подгруппу группы 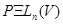 , а под проективной группой линейных преобразований пространства
, а под проективной группой линейных преобразований пространства  - любую подгруппу группы
- любую подгруппу группы  .
.
Для каждого ненулевого элемента  из
из 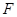 определим линейное преобразование
определим линейное преобразование  , полагая
, полагая

Ясно, что  . Преобразование
. Преобразование  из
из  вида
вида  для некоторого
для некоторого  будем называть растяжением пространства
будем называть растяжением пространства  . Множество растяжений пространства
. Множество растяжений пространства  является нормальной подгруппой группы
является нормальной подгруппой группы  , которая будет обозначаться через
, которая будет обозначаться через  . Очевидно, имеет место изоморфизм
. Очевидно, имеет место изоморфизм  . Имеют место следующие два предложения.
. Имеют место следующие два предложения.
Предложение Элемент  группы
группы  тогда и только тогда принадлежит группе
тогда и только тогда принадлежит группе  , когда
, когда  для всех прямых
для всех прямых  из
из  . В частности,
. В частности,
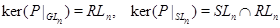
и

Предложение Централизатор в  любого элемента из
любого элемента из  , не являющегося растяжением, абелев.
, не являющегося растяжением, абелев.
Пусть теперь  - регулярное знакопеременное пространство. Тогда
- регулярное знакопеременное пространство. Тогда  будет, конечно, группой геометрических преобразований пространства
будет, конечно, группой геометрических преобразований пространства  . Под группой симплектических преобразований знакопеременного пространства
. Под группой симплектических преобразований знакопеременного пространства  мы будем понимать произвольную подгруппу из
мы будем понимать произвольную подгруппу из  . Группа
. Группа  , получаемая из
, получаемая из  применением гомоморфизма
применением гомоморфизма  , называется проективной симплектической группой знакопеременного пространства
, называется проективной симплектической группой знакопеременного пространства  . Под проективной группой симплектических преобразований пространства
. Под проективной группой симплектических преобразований пространства  будем понимать любую подгруппу группы
будем понимать любую подгруппу группы  .
.
Предложение Если  - ненулевое регулярное знакопеременное пространство, то
- ненулевое регулярное знакопеременное пространство, то

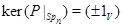
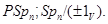
Доказательство является легким упражнением и потому опускается.
Предложение Если  - регулярное знакопеременное пространство и
- регулярное знакопеременное пространство и 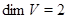 , то
, то  .
.
Доказательство. Взяв симплектическую базу пространства  , с помощью без труда убеждаемся, что элемент
, с помощью без труда убеждаемся, что элемент  из
из  тогда и только тогда лежит в
тогда и только тогда лежит в  , когда
, когда  .
.
Полярностью абстрактного векторного пространства  над полем
над полем  называется биекция
называется биекция 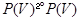 ,
,  , такая, что
, такая, что
1)  ,
,
2) 
для всех  ,
, 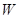 из
из  . Если
. Если  - регулярное знакопеременное пространство над
- регулярное знакопеременное пространство над  , то, очевидно,
, то, очевидно,  - полярность; она называется полярностью, определенной знакопеременной формой
- полярность; она называется полярностью, определенной знакопеременной формой 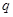 , имеющейся на
, имеющейся на  .
.
Предложение Пусть  - абстрактное векторное пространство над полем
- абстрактное векторное пространство над полем  и
и 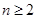 . Предположим, что
. Предположим, что  - регулярное знакопеременное пространство относительно каждой из двух знакопеременных форм
- регулярное знакопеременное пространство относительно каждой из двух знакопеременных форм  и
и  . Формы
. Формы  и
и  тогда и только тогда определяют одну и ту же полярность, когда найдется такой ненулевой элемент
тогда и только тогда определяют одну и ту же полярность, когда найдется такой ненулевой элемент  из
из  , что
, что  .
.
Доказательство. Если  , то утверждение очевидно. Остается доказать обратное утверждение. Так как
, то утверждение очевидно. Остается доказать обратное утверждение. Так как  регулярно относительно
регулярно относительно  и
и  , то ввиду и ассоциированные линейные отображения
, то ввиду и ассоциированные линейные отображения 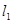 и
и  биективны, т. е.
биективны, т. е.  и
и  . Из и предположения о том, что
. Из и предположения о том, что  и
и  определяют одну и ту же полярность, следует, что
определяют одну и ту же полярность, следует, что  для всех подпространств
для всех подпространств  из
из  . Следовательно,
. Следовательно,  - элемент группы
- элемент группы  , относительно которого инвариантны все подпространства из
, относительно которого инвариантны все подпространства из  , В частности, относительно него инвариантны все прямые из
, В частности, относительно него инвариантны все прямые из  . Значит, ввиду
. Значит, ввиду  . Другими словами, найдется такой ненулевой элемент
. Другими словами, найдется такой ненулевой элемент  из
из  , что
, что  для всех
для всех  из
из  . Но тогда
. Но тогда 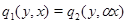 для всех
для всех  из
из  . Поэтому
. Поэтому  .
.
|
из
5.00
|
Обсуждение в статье: Проективные преобразования |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

