 |
Главная |
Знакопеременные пространства
|
из
5.00
|
Векторное пространство  над полем
над полем  называется знакопеременным, если на нем задана знакопеременная билинейная форма
называется знакопеременным, если на нем задана знакопеременная билинейная форма  , т. е. отображение
, т. е. отображение 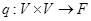 со следующими свойствами:
со следующими свойствами:

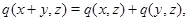


для всех 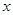 ,
,  ,
,  из
из  и всех
и всех  из
из 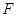 . Отметим следствие этих соотношений:
. Отметим следствие этих соотношений:

Если  - знакопеременная форма и
- знакопеременная форма и  - произвольный элемент из
- произвольный элемент из 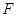 , то отображение
, то отображение  , определенное формулой
, определенное формулой 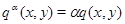 , также знакопеременно, и сложный объект, являющийся исходным векторным пространством
, также знакопеременно, и сложный объект, являющийся исходным векторным пространством  с этой новой формой
с этой новой формой  , будет знакопеременным пространством, которое мы обозначим через
, будет знакопеременным пространством, которое мы обозначим через  .
.
Представление знакопеременного пространства  в знакопеременное пространство
в знакопеременное пространство  (оба над полем
(оба над полем 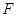 и с формами, обозначаемыми через
и с формами, обозначаемыми через  ) есть по определению линейное преобразование
) есть по определению линейное преобразование  пространства
пространства  в
в  , такое, что
, такое, что  для всех
для всех 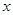 ,
,  . Инъективное представление называется изометрией
. Инъективное представление называется изометрией  в
в  . Пространства
. Пространства  и
и  называются изометричными, если существует изометрия
называются изометричными, если существует изометрия  на
на  . Пусть
. Пусть  обозначает представление,
обозначает представление,  - изометрию ``в'', а
- изометрию ``в'', а  или
или  - изометрию ``на''. Очевидно, что композиция двух изометрии - изометрия и преобразование, обратное к изометрии, - также изометрия. В частности, множество изометрий пространства
- изометрию ``на''. Очевидно, что композиция двух изометрии - изометрия и преобразование, обратное к изометрии, - также изометрия. В частности, множество изометрий пространства  на себя является подгруппой общей линейной группы
на себя является подгруппой общей линейной группы  абстрактного векторного пространства
абстрактного векторного пространства  ; она называется симплектической группой знакопеременного пространства
; она называется симплектической группой знакопеременного пространства  и обозначается через
и обозначается через  . Для любого ненулевого элемента
. Для любого ненулевого элемента  из
из  имеем
имеем 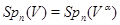 .
.
Предложение Пусть  - линейное преобразование знакопеременного пространства
- линейное преобразование знакопеременного пространства  в знакопеременное пространство
в знакопеременное пространство  . Предположим, что существует база
. Предположим, что существует база  пространства
пространства  , такая, что
, такая, что  для всех
для всех  ,
, 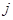 . Тогда
. Тогда  -- представление.
-- представление.
Доказательство. Это тривиально следует из определений.
Каждому знакопеременному пространству  со знакопеременной формой
со знакопеременной формой  сопоставим отображения
сопоставим отображения  и
и  пространства
пространства  в сопряженное пространство
в сопряженное пространство  (
(  рассматривается как абстрактное векторное пространство над
рассматривается как абстрактное векторное пространство над  ). По определению отображение
). По определению отображение  сопоставляет произвольному элементу
сопоставляет произвольному элементу 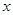 из
из  линейный функционал
линейный функционал  , определенный формулой
, определенный формулой  , а
, а  переводит
переводит 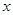 в
в  . Легко проверяется, что
. Легко проверяется, что  и
и  являются линейными преобразованиями.
являются линейными преобразованиями.
 - матрица
- матрица  над
над  называется кососимметрической, если
называется кососимметрической, если  , и знакопеременной, если
, и знакопеременной, если  и на главной диагонали стоят нули. Таким образом, знакопеременные матрицы являются кососимметрическими. Обратно, кососимметрические матрицы являются знакопеременными, если характеристика поля
и на главной диагонали стоят нули. Таким образом, знакопеременные матрицы являются кососимметрическими. Обратно, кососимметрические матрицы являются знакопеременными, если характеристика поля  не равна
не равна  . Рассмотрим знакопеременное пространство
. Рассмотрим знакопеременное пространство  . Мы можем ассоциировать с базой
. Мы можем ассоциировать с базой  пространства
пространства  матрицу, у которой на месте
матрицу, у которой на месте  стоит
стоит  . Назовем
. Назовем  матрицей знакопеременного пространства
матрицей знакопеременного пространства  в базе
в базе  и будем писать
и будем писать

Если существует хотя бы одна база, в которой  имеет матрицу
имеет матрицу  , то будем писать
, то будем писать 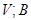 . Матрица
. Матрица  , ассоциированная со знакопеременным пространством
, ассоциированная со знакопеременным пространством  указанным способом, является, очевидно, знакопеременной. Что происходит при изменении базы? Предположим, что
указанным способом, является, очевидно, знакопеременной. Что происходит при изменении базы? Предположим, что 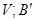 в базе
в базе  и
и  - матрица перехода от первой базы ко второй, т. е.
- матрица перехода от первой базы ко второй, т. е.

Тогда

откуда видно, что изменение матрицы пространства  при изменении базы описывается соотношением
при изменении базы описывается соотношением  .
.
Если  - абстрактное векторное пространство с базой
- абстрактное векторное пространство с базой  и
и  - произвольная знакопеременная
- произвольная знакопеременная  -матрица над
-матрица над  , то существует единственный способ превратить
, то существует единственный способ превратить  в знакопеременное пространство, такое, что
в знакопеременное пространство, такое, что  в
в  , а именно, положить
, а именно, положить
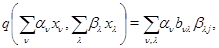
где  - элемент, стоящий в матрице
- элемент, стоящий в матрице  на месте
на месте  .
.
Предложение Предположим, что  - знакопеременное пространство,
- знакопеременное пространство,  - его база и
- его база и 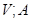 в
в 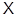 . Тогда матричный изоморфизм, определенный базой
. Тогда матричный изоморфизм, определенный базой  , отображает
, отображает  на группу всех обратимых
на группу всех обратимых  -матриц
-матриц  над
над  , удовлетворяющих соотношению
, удовлетворяющих соотношению

Дискриминантом  векторов
векторов 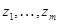 в знакопеременном пространстве
в знакопеременном пространстве  называется определитель
называется определитель

В частности, если  - база пространства
- база пространства  и
и 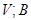 в этой базе, то
в этой базе, то

Если  - другая база, то соотношение
- другая база, то соотношение  показывает, что
показывает, что

для некоторого  из
из  . Следовательно, канонический образ элемента
. Следовательно, канонический образ элемента  в
в  не зависит от базы; он называется дискриминантом знакопеременного пространства
не зависит от базы; он называется дискриминантом знакопеременного пространства  и обозначается через
и обозначается через  . Здесь множество
. Здесь множество  определяется очевидным образом: берем факторгруппу
определяется очевидным образом: берем факторгруппу  , присоединяем к ней нуль 0 и полагаем, что произведение нуля и любого другого элемента равно нулю. Запись
, присоединяем к ней нуль 0 и полагаем, что произведение нуля и любого другого элемента равно нулю. Запись  , где
, где  , будет обозначать, что
, будет обозначать, что  равно каноническому образу элемента
равно каноническому образу элемента  в
в  или, другими словами, что
или, другими словами, что  обладает базой
обладает базой  , для которой
, для которой  . Если
. Если  , то полагаем
, то полагаем  .
.
Пример Рассмотрим знакопеременное пространство  со знакопеременной формой
со знакопеременной формой  . Пусть
. Пусть  - его база, а
- его база, а  - сопряженная база сопряженного пространства
- сопряженная база сопряженного пространства  . Пусть
. Пусть 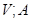 в
в 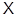 . Тогда
. Тогда  . Легко видеть, что матрица линейного преобразования
. Легко видеть, что матрица линейного преобразования  , определенного ранее, относительно баз
, определенного ранее, относительно баз 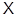 и
и  равна
равна  ; действительно, если
; действительно, если 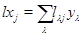 , то
, то

Аналогично матрица преобразования  относительно баз
относительно баз  и
и  равна
равна  .
.
Предложение Любые 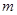 векторов
векторов 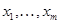 знакопеременного пространства
знакопеременного пространства  , такие, что
, такие, что  , линейно независимы.
, линейно независимы.
Доказательство. Зависимость  влечет за собой
влечет за собой  для
для 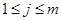 . Это означает зависимость между строками матрицы
. Это означает зависимость между строками матрицы  , что невозможно, так как дискриминант не равен 0.
, что невозможно, так как дискриминант не равен 0.
Предложение Следующие утверждения для знакопеременного пространства  равносильны:
равносильны:
•  ,
,
•  ,
,
• 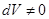 ,
,
•  биективно,
биективно,
•  биективно.
биективно.
Доказательство. Можно считать, что  . Зафиксируем базу
. Зафиксируем базу  пространства
пространства  , и пусть
, и пусть  - сопряженная база. Пусть
- сопряженная база. Пусть 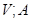 в
в 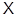 . Ввиду
. Ввиду
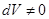
| 
|
 обратима обратима 
| |
 биективно, биективно,
|
поэтому (3) равносильно (5). Аналогично (3) равносильно (4). Далее
 биективно биективно
| 
|

| |

| |

| |
 , ,
|
так что (5) равносильно (2). Наконец, очевидно, что (2) равносильно (1).
Определение Знакопеременное пространство  называется регулярным, если оно удовлетворяет одному из пяти равносильных условий . Знакопеременное пространство
называется регулярным, если оно удовлетворяет одному из пяти равносильных условий . Знакопеременное пространство  называется вырожденным, если оно не является регулярным. Наконец, оно называется вполне вырожденным, если
называется вырожденным, если оно не является регулярным. Наконец, оно называется вполне вырожденным, если  .
.
Если  , то
, то  регулярно. Если
регулярно. Если  , то ввиду и
, то ввиду и

Предложение Пусть 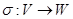 - представление знакопеременных пространств. Если
- представление знакопеременных пространств. Если  регулярно, то
регулярно, то  - изометрия.
- изометрия.
Доказательство. Возьмем  из ядра представления
из ядра представления  . Тогда
. Тогда  . Отсюда ввиду регулярности пространства
. Отсюда ввиду регулярности пространства  получаем, что
получаем, что  .
.
Предложение Каждой базе  регулярного знакопеременного пространства
регулярного знакопеременного пространства  соответствует единственная база
соответствует единственная база  этого пространства, называемая сопряженной к
этого пространства, называемая сопряженной к 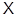 относительно
относительно 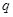 и такая, что
и такая, что  для всех
для всех  ,
,  . Если
. Если 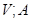 в
в 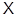 и
и 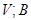 в
в  , то
, то  .
.
Доказательство. 1) Положим  для
для  , где
, где  - сопряженная к
- сопряженная к  база сопряженного пространства
база сопряженного пространства 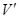 . Тогда
. Тогда  - база, так как
- база, так как  биективно. Кроме того,
биективно. Кроме того,

Этим доказано существование базы  . Единственность непосредственно следует из регулярности.
. Единственность непосредственно следует из регулярности.
2) Пусть  . Тогда
. Тогда  и
и

Отсюда  , так что
, так что  и
и  .
.
Рассмотрим знакопеременное пространство  со знакопеременной формой
со знакопеременной формой 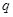 . Будем говорить, что
. Будем говорить, что  имеет ортогональное разложение
имеет ортогональное разложение

на подпространства  если оно является прямой суммой
если оно является прямой суммой  с попарно ортогональными
с попарно ортогональными  , т. е.
, т. е.  при
при  . Назовем
. Назовем  компонентами этого ортогонального разложения. Будем говорить, что подпространство
компонентами этого ортогонального разложения. Будем говорить, что подпространство  расщепляет
расщепляет  или что
или что  является компонентой пространства
является компонентой пространства  , если существует подпространство
, если существует подпространство 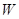 пространства
пространства  , такое, что
, такое, что  . Имеем
. Имеем

где произведение берется в  .
.
Рассмотрим два знакопеременных пространства  и
и 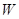 над одним и тем же полем
над одним и тем же полем  и предположим, что имеется ортогональное разложение
и предположим, что имеется ортогональное разложение  , а
, а 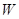 - сумма пространств
- сумма пространств  ,
, 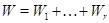 , причем
, причем  при
при  . Пусть для каждого
. Пусть для каждого  ,
,  , задано представление
, задано представление  . Тогда, как известно из линейной алгебры, существует единственное линейное преобразование
. Тогда, как известно из линейной алгебры, существует единственное линейное преобразование 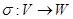 , согласующееся с каждым
, согласующееся с каждым  на
на  . На самом деле легко проверить, что
. На самом деле легко проверить, что 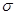 - представление. Мы будем записывать его в виде
- представление. Мы будем записывать его в виде

Важным является случай, когда  ,
,  для всех
для всех  и
и  для всех
для всех  ; тогда
; тогда

Если дано еще одно такое представление  , то
, то

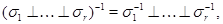

Рассмотрим знакопеременное пространство  над полем
над полем  . Под ортогональным дополнением подпространства
. Под ортогональным дополнением подпространства  пространства
пространства  в
в  понимается подпространство
понимается подпространство

совпадающее также с

Определим радикал пространства  как подпространство
как подпространство  . Очевидно,
. Очевидно,
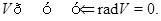
Предложение Пусть  - знакопеременное пространство, являющееся суммой попарно ортогональных подпространств, т. е.
- знакопеременное пространство, являющееся суммой попарно ортогональных подпространств, т. е.  , где
, где  при
при  . Тогда
. Тогда
•  ,
,
•  регулярно
регулярно  каждое
каждое  регулярно,
регулярно,
•  регулярно
регулярно  .
.
Доказательство. (1) Возьмем в  произвольный элемент
произвольный элемент  и запишем его в виде
и запишем его в виде 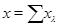 ,
,  . Тогда
. Тогда

так что  , откуда
, откуда  . Обратно, если
. Обратно, если 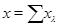 , где
, где  , то
, то

откуда  .
.
(2) Это следует из (1) и того, что знакопеременное пространство регулярно тогда и только тогда, когда его радикал равен  .
.
(3) Если  ,
,  , то
, то
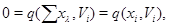
откуда  . Следовательно,
. Следовательно,  и, значит,
и, значит,  .
.
Предложение Если  - подпространство знакопеременного пространства
- подпространство знакопеременного пространства  , то
, то  - аннулятор пространства
- аннулятор пространства  в
в  , т. е.
, т. е.  . В частности,
. В частности,  .
.
Доказательство непосредственно следует из определений.
Предложение Пусть  - регулярное подпространство знакопеременного пространства
- регулярное подпространство знакопеременного пространства  . Тогда
. Тогда  расщепляет
расщепляет  , точнее,
, точнее,  . Если
. Если  - другое расщепление,
- другое расщепление, 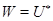 .
.
Доказательство. Так как  регулярно, то
регулярно, то  . Следовательно, ввиду
. Следовательно, ввиду

Поэтому  и, значит,
и, значит,  . Далее, если
. Далее, если  , то
, то  , откуда
, откуда 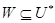 . Сравнивая размерности, получаем
. Сравнивая размерности, получаем  .
.
Предложение Если  и
и 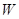 - произвольные подпространства регулярного знакопеременного пространства
- произвольные подпространства регулярного знакопеременного пространства  размерности
размерности 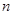 , то
, то
•  ,
,
•  ,
,
•  ,
,
• 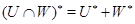 ,
,
•  .
.
Доказательство. Так как  регулярно, то ввиду отображение
регулярно, то ввиду отображение  биективно. Следовательно,
биективно. Следовательно,  , откуда ввиду
, откуда ввиду  . Этим доказано (1). Далее,
. Этим доказано (1). Далее, 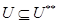 , поэтому сравнение размерностей дает
, поэтому сравнение размерностей дает  . Этим доказано (2). Докажем теперь (3):
. Этим доказано (2). Докажем теперь (3):
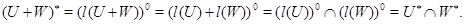
Аналогично доказывается (4). Наконец, утверждение (5) тривиально.
Рассмотрим радикал  знакопеременного пространства
знакопеременного пространства  , и пусть
, и пусть  - подпространство пространства
- подпространство пространства  , такое, что
, такое, что  . Назовем всякое такое разложение радикальным разложением пространства
. Назовем всякое такое разложение радикальным разложением пространства  . Очевидно,
. Очевидно,  определяется не единственным образом, за исключением случаев, когда
определяется не единственным образом, за исключением случаев, когда  регулярно или вполне вырождено. Из соотношений
регулярно или вполне вырождено. Из соотношений

следует равенство  , поэтому
, поэтому  регулярно.
регулярно.
Теорема Если 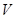 - регулярное знакопеременное пространство размерности
- регулярное знакопеременное пространство размерности  , то
, то

В частности, регулярное знакопеременное пространство имеет четную размерность и дискриминант  . Кроме того, регулярные знакопеременные пространства одинаковой размерности над одним и тем же полем
. Кроме того, регулярные знакопеременные пространства одинаковой размерности над одним и тем же полем  изометричны.
изометричны.
Доказательство. Ввиду регулярности пространства 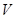 существуют векторы
существуют векторы  и
и  , удовлетворяющие условию
, удовлетворяющие условию  . Так как
. Так как 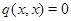 , то эти векторы должны быть независимыми; поэтому
, то эти векторы должны быть независимыми; поэтому  - плоскость. Очевидно,
- плоскость. Очевидно,

В частности,  регулярно, так как дискриминант отличен от нуля. Следовательно, ввиду
регулярно, так как дискриминант отличен от нуля. Следовательно, ввиду  . Но
. Но  - также регулярное знакопеременное пространство. Первое утверждение следует теперь из соображений индукции. Второе тривиально следует из первого. Для доказательства третьего утверждения применяем . Теорема доказана.
- также регулярное знакопеременное пространство. Первое утверждение следует теперь из соображений индукции. Второе тривиально следует из первого. Для доказательства третьего утверждения применяем . Теорема доказана.
База  регулярного знакопеременного пространства
регулярного знакопеременного пространства  называется гиперболической, если
называется гиперболической, если

и симплектической, если

Если

- гиперболическая база пространства 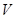 , то перестановка
, то перестановка

- симплектическая база, и наоборот. По теореме ненулевое регулярное знакопеременное пространство имеет гиперболическую базу, а потому и симплектическую базу.
Предложение Пусть 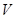 - регулярное знакопеременное пространство,
- регулярное знакопеременное пространство,  - вполне вырожденное подпространство и
- вполне вырожденное подпространство и  - база подпространства
- база подпространства  . Тогда существует регулярное подпространство
. Тогда существует регулярное подпространство  пространства
пространства  вида
вида  , где
, где  - регулярные плоскости и
- регулярные плоскости и  ,
,  .
.
Доказательство. Случай  очевиден. При
очевиден. При  применяем индукцию по
применяем индукцию по  . Положим
. Положим 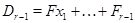 и
и  . Тогда
. Тогда  , откуда
, откуда  ввиду . Выберем
ввиду . Выберем  и положим
и положим  . Тогда
. Тогда  ,
,  , и, следовательно,
, и, следовательно,  . Значит,
. Значит,  - регулярная плоскость, содержащая
- регулярная плоскость, содержащая  . В силу можно записать
. В силу можно записать  . Тогда
. Тогда 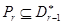 , так как
, так как


