 |
Главная |
Структурные теоремы. Порядки симплектических групп
|
из
5.00
|
Предложение Если поле  бесконечно, то группы
бесконечно, то группы 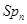 ,
,  над
над  также бесконечны.
также бесконечны.
Доказательство. Число трансвекций 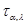 из
из 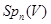 бесконечно.
бесконечно.
Теорема Порядок группы  равен
равен
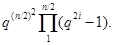
Порядок группы  равен
равен
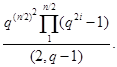
Доказательство. Второе утверждение следует из первого, так как группа  изоморфна группе
изоморфна группе  . Докажем первое утверждение индукцией по
. Докажем первое утверждение индукцией по  . Если
. Если  , то
, то  и можно считать
и можно считать  .
.
Под парой будем понимать упорядоченную пару векторов  ,
,  , такую, что
, такую, что  . Если
. Если 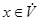 фиксирован, то существует единственная пара
фиксирован, то существует единственная пара 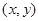 , где
, где  принадлежит данной прямой, не ортогональной к
принадлежит данной прямой, не ортогональной к  . Поэтому число пар с
. Поэтому число пар с  на первом месте равно числу прямых, не лежащих в
на первом месте равно числу прямых, не лежащих в 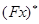 , т. е.
, т. е.

Таким образом, имеется  пар с
пар с  на первом месте, а всего
на первом месте, а всего  пар.
пар.
Зафиксируем какую-нибудь пару  . По теореме Витта для каждой пары
. По теореме Витта для каждой пары  найдется по крайней мере один элемент группы
найдется по крайней мере один элемент группы  , переводящий
, переводящий  в
в  . Следовательно, имеется точно
. Следовательно, имеется точно

элементов из  , переводящих пару
, переводящих пару  в пару
в пару 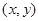 . По предположению индукции это число равно
. По предположению индукции это число равно
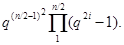
Далее, каждый элемент группы  переводит
переводит  точно в одну пару. Следовательно, группа
точно в одну пару. Следовательно, группа  содержит
содержит

элементов, что и требовалось доказать.
Предложение Если  , то число максимальных вполне вырожденных подпространств пространства
, то число максимальных вполне вырожденных подпространств пространства  равно
равно

Доказательство. 1) Покажем сначала, что подгруппа  группы
группы 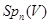 , оставляющая на месте произвольное максимальное вполне вырожденное подпространство
, оставляющая на месте произвольное максимальное вполне вырожденное подпространство  пространства
пространства  , имеет порядок
, имеет порядок

Чтобы убедиться в этом, зафиксируем симплектическую базу

пространства  , в которой векторы
, в которой векторы  порождают
порождают  . Из следует, что матрица произвольного преобразования
. Из следует, что матрица произвольного преобразования  имеет вид
имеет вид

где  , а
, а 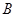 - симметрическая матрица порядка
- симметрическая матрица порядка  над
над  ; эти
; эти  и
и  определяются преобразованием
определяются преобразованием  однозначно. Кроме того, любые такие
однозначно. Кроме того, любые такие  и
и  соответствуют некоторому
соответствуют некоторому  из
из  . Наше утверждение получается теперь, если умножить порядок группы
. Наше утверждение получается теперь, если умножить порядок группы  на число симметрических матриц порядка
на число симметрических матриц порядка  над полем
над полем  , т. е.
, т. е.  .
.
2) Зафиксируем максимальное вполне вырожденное подпространство 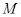 пространства
пространства  . По теореме Витта все максимальные вполне вырожденные подпространства пространства
. По теореме Витта все максимальные вполне вырожденные подпространства пространства  даются формулой
даются формулой  , где
, где  пробегает группу
пробегает группу  . Из замечания 1) легко следует, что в этом процессе каждое максимальное вполне вырожденное подпространство повторяется точно
. Из замечания 1) легко следует, что в этом процессе каждое максимальное вполне вырожденное подпространство повторяется точно
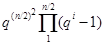
раз, поэтому общее число таких подпространств равно порядку группы 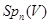 , деленному на указанную величину. Очевидно, это и есть требуемое число.
, деленному на указанную величину. Очевидно, это и есть требуемое число.
Предложение Если  , то число регулярных плоскостей в пространстве
, то число регулярных плоскостей в пространстве  равно
равно

Доказательство. Поступая, как при доказательстве утверждения , убедимся, что  должно содержать
должно содержать

регулярных плоскостей. Это число совпадает с указанным выше (применить теорему ).
Предложение Группа 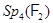 изоморфна симметрической группе
изоморфна симметрической группе 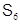 .
.
Доказательство. Будем называть конфигурацией произвольное подмножество  из
из  элементов в
элементов в  -мерном регулярном знакопеременном пространстве
-мерном регулярном знакопеременном пространстве 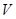 над полем
над полем 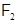 , обладающее тем свойством, что любые два его различных элемента не ортогональны. Каждый ненулевой вектор
, обладающее тем свойством, что любые два его различных элемента не ортогональны. Каждый ненулевой вектор  из
из  принадлежит ровно двум конфигурациям
принадлежит ровно двум конфигурациям  и
и  , так что они пересекаются по
, так что они пересекаются по 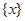 . Чтобы убедиться в этом, возьмем симплектическую базу
. Чтобы убедиться в этом, возьмем симплектическую базу  пространства
пространства 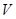 , в которой
, в которой  . Ясно, что
. Ясно, что
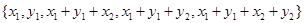
и

- две различные конфигурации, пересекающиеся по множеству  . Легкая проверка перебором показывает, что других конфигураций, содержащих элемент
. Легкая проверка перебором показывает, что других конфигураций, содержащих элемент  , нет. Если теперь выписать все различные конфигурации
, нет. Если теперь выписать все различные конфигурации 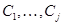 в пространстве
в пространстве 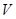 , то каждый вектор
, то каждый вектор 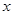 из
из  появится точно в двух из них, откуда
появится точно в двух из них, откуда 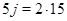 и
и  . Пусть
. Пусть  - Множество всех конфигураций в
- Множество всех конфигураций в  .
.
Если  - произвольный элемент из
- произвольный элемент из  , то
, то 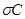 тогда и только тогда является конфигурацией, когда
тогда и только тогда является конфигурацией, когда  - конфигурация, поэтому
- конфигурация, поэтому  индуцирует отображение
индуцирует отображение  . Ясно, что это отображение на и, значит, перестановка на
. Ясно, что это отображение на и, значит, перестановка на  . Очевидно, что
. Очевидно, что 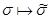 есть гомоморфное отображение
есть гомоморфное отображение  . Чтобы найти его ядро, возьмем в
. Чтобы найти его ядро, возьмем в  элемент
элемент  . Пусть
. Пусть  таков, что
таков, что  . Пусть
. Пусть  и
и  - две конфигурации, содержащие
- две конфигурации, содержащие  . Тогда
. Тогда 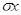 не принадлежит одной из них, скажем,
не принадлежит одной из них, скажем,  . Отсюда
. Отсюда  и
и  . Другими словами, ядро тривиально, и мы имеем инъективный гомоморфизм
. Другими словами, ядро тривиально, и мы имеем инъективный гомоморфизм  . По теореме группа
. По теореме группа  состоит из
состоит из  элементов, поэтому
элементов, поэтому 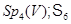 .
.
Центры
Заметим, что группа  неабелева. Чтобы убедиться в этом, достаточно взять нетривиальные проективные трансвекции из
неабелева. Чтобы убедиться в этом, достаточно взять нетривиальные проективные трансвекции из  с неортогональными вычетными прямыми. Следовательно, группа
с неортогональными вычетными прямыми. Следовательно, группа  также неабелева.
также неабелева.
Предложение Группа  имеет тривиальный центр, а
имеет тривиальный центр, а  .
.
Доказательство. Рассмотрим произвольный элемент  из центра группы
из центра группы  . Пусть
. Пусть  - произвольная прямая из
- произвольная прямая из  . Пусть
. Пусть  - проективная трансвекция из
- проективная трансвекция из  с вычетной прямой
с вычетной прямой 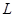 . Тогда вычетной прямой преобразования
. Тогда вычетной прямой преобразования  является
является  . Но
. Но  , так как
, так как  лежит в центре. Следовательно,
лежит в центре. Следовательно,  для всех
для всех  . Поэтому
. Поэтому  и, значит, группа
и, значит, группа  действительно не имеет центра. Второе утверждение следует из первого, если применить гомоморфизм
действительно не имеет центра. Второе утверждение следует из первого, если применить гомоморфизм  .
.
Коммутанты
Предложение Если  ,
,  - произвольные прямые из
- произвольные прямые из 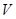 , то множество трансвекций из
, то множество трансвекций из  с вычетной прямой
с вычетной прямой  и множество трансвекций с вычетной прямой
и множество трансвекций с вычетной прямой  сопряжены относительно
сопряжены относительно  .
.
Доказательство. По теореме Витта в группе 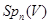 существует такой элемент
существует такой элемент  , что
, что  . Тогда сопряжение элементом
. Тогда сопряжение элементом  отображает множество трансвекций из
отображает множество трансвекций из  с вычетной прямой
с вычетной прямой  на множество трансвекций из
на множество трансвекций из  с вычетной прямой
с вычетной прямой  .
.
Пример Две трансвекций из 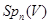 не обязательно сопряжены в
не обязательно сопряжены в  . Например, трансвекций с вычетной прямой
. Например, трансвекций с вычетной прямой  , сопряженные с
, сопряженные с  , имеют вид
, имеют вид  , где
, где  пробегает
пробегает  .
.
Замечание Пусть  - симплектическая база пространства
- симплектическая база пространства 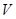 . Если
. Если  - произвольная симметрическая матрица порядка
- произвольная симметрическая матрица порядка 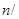 2 над
2 над 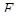 и
и  - линейное преобразование, определенное матрицей
- линейное преобразование, определенное матрицей

то мы знаем, что  принадлежит группе
принадлежит группе  . Если преобразовать
. Если преобразовать  в
в  , производя 1) прибавление кратного одного столбца к другому с последующим аналогичным преобразованием соответствующих строк или 2) перестановку двух столбцов с последующей перестановкой соответствующих строк, то линейное преобразование
, производя 1) прибавление кратного одного столбца к другому с последующим аналогичным преобразованием соответствующих строк или 2) перестановку двух столбцов с последующей перестановкой соответствующих строк, то линейное преобразование  с матрицей
с матрицей

снова будет принадлежать группе  , так как
, так как  тоже будет симметрической. В действительности
тоже будет симметрической. В действительности  и
и  сопряжены в
сопряжены в  . Чтобы убедиться в этом, заметим, что
. Чтобы убедиться в этом, заметим, что  при подходящей матрице
при подходящей матрице 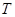 из
из  . Преобразование
. Преобразование  , определенное матрицей
, определенное матрицей

принадлежит группе  , и
, и  , так как
, так как

Предложение Предположим, что  ,
,  ,
,  и пусть
и пусть  - нормальная подгруппа группы
- нормальная подгруппа группы  , содержащая регулярный элемент
, содержащая регулярный элемент  с вычетом
с вычетом 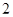 , представимый в виде произведения двух трансвекций из
, представимый в виде произведения двух трансвекций из 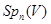 . Тогда
. Тогда  .
.
Доказательство. Имеем разложение 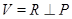 , где
, где  - регулярная плоскость. Рассмотрим группу
- регулярная плоскость. Рассмотрим группу

Тогда  . Кроме того,
. Кроме того,  . Это очевидно, если
. Это очевидно, если  ; если же
; если же  , то применяем 2.1.12 и теорему 2.1.11 . Поэтому
, то применяем 2.1.12 и теорему 2.1.11 . Поэтому  - нормальная подгруппа в
- нормальная подгруппа в  , не содержащаяся в
, не содержащаяся в  . Отсюда следует, что
. Отсюда следует, что  . В частности, если
. В частности, если  - фиксированная прямая в
- фиксированная прямая в  , то
, то 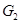 содержит все трансвекции плоскости
содержит все трансвекции плоскости  с вычетной прямой
с вычетной прямой  . Следовательно,
. Следовательно,  содержит все трансвекции из
содержит все трансвекции из  с вычетной прямой
с вычетной прямой  , а потому в силу вообще все трансвекции из
, а потому в силу вообще все трансвекции из  и
и  .
.
Предложение Предположим, что  ,
, 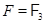 или
или  ,
,  , и пусть
, и пусть  - нормальная подгруппа группы
- нормальная подгруппа группы  , содержащая вырожденный элемент
, содержащая вырожденный элемент  с вычетом 2, представимый в виде произведения двух трансвекций из
с вычетом 2, представимый в виде произведения двух трансвекций из  . Тогда
. Тогда  .
.
Доказательство. 1) Модификация рассуждений, использованных при доказательстве утверждения , позволяет считать, что  , если
, если  , и
, и  , если
, если 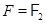 .
.
2) Рассмотрим сначала случай  ,
,  . Тогда
. Тогда  имеет вид
имеет вид  , причем
, причем  , а звездочки равны
, а звездочки равны 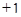 . Далее эти трансвекции перестановочны, так как
. Далее эти трансвекции перестановочны, так как  , поэтому мы можем, если нужно, заменить
, поэтому мы можем, если нужно, заменить  на
на 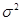 и считать, что на самом деле
и считать, что на самом деле  . Можно считать, что эта новая
. Можно считать, что эта новая  есть
есть  . В самом деле, если
. В самом деле, если  , то с помощью теоремы Витта выберем такое
, то с помощью теоремы Витта выберем такое  , что
, что 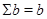 ,
,  . Тогда
. Тогда

Заменим теперь  на
на
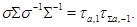
Итак, можно считать, что  . Дополним
. Дополним 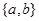 до симплектической базы
до симплектической базы
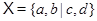
пространства  и заметим, что
и заметим, что

Подходящим сопряжением мы можем найти в 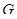 линейные преобразования с матрицами
линейные преобразования с матрицами

в базе  . Произведение этих преобразований равно элементу из
. Произведение этих преобразований равно элементу из 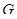 с матрицей
с матрицей
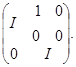
Следовательно, группа  содержит
содержит  . Таким образом, она содержит все (= обе) трансвекции из
. Таким образом, она содержит все (= обе) трансвекции из  с вычетной прямой
с вычетной прямой  . Ввиду отсюда следует, что
. Ввиду отсюда следует, что 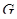 содержит все трансвекции из
содержит все трансвекции из  и, значит,
и, значит,  .
.
3) Пусть теперь  ,
,  . Тогда
. Тогда  и
и 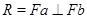 . Дополним
. Дополним  до симплектической базы
до симплектической базы

Тогда

Сопряжение дает нам в  линейные преобразования с матрицами
линейные преобразования с матрицами

а потому и с матрицами

а значит, и с матрицей

Другими словами,  содержит
содержит  и, следовательно, все трансвекции из
и, следовательно, все трансвекции из  , откуда
, откуда  .
.
Предложение Если 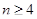 , то
, то  за одним исключением:
за одним исключением:  .
.
Доказательство. Пусть  , для некоторого
, для некоторого  . По теореме Витта существует такое
. По теореме Витта существует такое  , что
, что  - плоскость и
- плоскость и

Положим

Осталось применить и . В исключительном случае применяем и хорошо известные свойства группы  .
.
Предложение Если 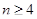 , то
, то 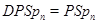 за одним исключением:
за одним исключением:  .
.
Теоремы о простоте
Теорема Для любого четного числа 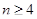 и любого поля
и любого поля  группа
группа 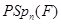 проста за исключением группы
проста за исключением группы  , которая простой не является.
, которая простой не является.
Доказательство. 1) Исключительное поведение группы  следует из . Будем предполагать поэтому, что
следует из . Будем предполагать поэтому, что  в общем случае и
в общем случае и  при
при 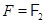 . Вместо проективной группы мы будем иметь дело с группой
. Вместо проективной группы мы будем иметь дело с группой  . Достаточно рассмотреть нормальную подгруппу
. Достаточно рассмотреть нормальную подгруппу  группы
группы  , не содержащуюся в подгруппе
, не содержащуюся в подгруппе  , и доказать, что
, и доказать, что  .
.
2) Сначала покажем, что имеются  ,
,  , такие, что
, такие, что  - регулярная плоскость. Для этого возьмем в группе
- регулярная плоскость. Для этого возьмем в группе  элемент
элемент  .
.  сдвигает по крайней мере одну прямую из
сдвигает по крайней мере одну прямую из  , т. е. существует такая прямая
, т. е. существует такая прямая  из
из  , что
, что  . Пусть
. Пусть 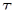 - нетривиальная трансвекция из
- нетривиальная трансвекция из  с вычетной прямой
с вычетной прямой  . Тогда элемент
. Тогда элемент

принадлежит группе 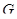 и является произведением двух трансвекции из
и является произведением двух трансвекции из  с различными вычетными прямыми
с различными вычетными прямыми  и
и  . Поэтому вычетное пространство преобразования
. Поэтому вычетное пространство преобразования  есть плоскость
есть плоскость  , в частности,
, в частности,  . Если
. Если  - гиперболическое преобразование, то
- гиперболическое преобразование, то  - инволюция. Применим теперь утверждение 1.18, если характеристика равна
- инволюция. Применим теперь утверждение 1.18, если характеристика равна  , и утверждение 1.13, если характеристика не равна
, и утверждение 1.13, если характеристика не равна  . Тогда, в частности, мы получим, что
. Тогда, в частности, мы получим, что  не является произведением
не является произведением 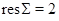 трансвекции из
трансвекции из  , что противоречит допущению. Итак,
, что противоречит допущению. Итак,  не может быть гиперболическим. Значит, существует такой вектор
не может быть гиперболическим. Значит, существует такой вектор  , что
, что  , т. е.
, т. е.  - регулярная плоскость.
- регулярная плоскость.
3) Можно также показать, что имеются вектор  и преобразование
и преобразование  , такие, что
, такие, что  - вырожденная плоскость. В самом деле, возьмем в
- вырожденная плоскость. В самом деле, возьмем в  элемент
элемент  . Существует такой вектор
. Существует такой вектор  , что
, что  . Если
. Если  , то цель достигнута, поэтому будем считать, что
, то цель достигнута, поэтому будем считать, что  . Выберем
. Выберем  так, чтобы было
так, чтобы было

По теореме Витта в  найдется преобразование
найдется преобразование  , такое, что
, такое, что  ,
,  . Тогда преобразование
. Тогда преобразование  принадлежит
принадлежит 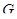 и переводит
и переводит 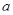 в
в  , поэтому
, поэтому  - вырожденная плоскость.
- вырожденная плоскость.
4) Возьмем  ,
,  так, чтобы плоскость
так, чтобы плоскость  была регулярной при
была регулярной при  и вырожденной при
и вырожденной при 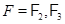 . Тогда преобразование
. Тогда преобразование

принадлежит группе  , является произведением двух трансвекций из
, является произведением двух трансвекций из  и его вычетное пространство есть плоскость
и его вычетное пространство есть плоскость  . Поэтому
. Поэтому  .
.
Предложение Если  и
и  - нормальная подгруппа группы
- нормальная подгруппа группы  , то
, то  или
или 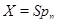 , за исключением группы
, за исключением группы 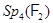 , которая, очевидно, не обладает этим свойством.
, которая, очевидно, не обладает этим свойством.
Доказательство. По поводу исключения см. . Далее, применяя к  теорему , получим, что
теорему , получим, что  или
или 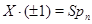 . Допустим последнее. Тогда
. Допустим последнее. Тогда
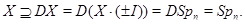
Предложение доказано.
Теорему о простоте можно также доказать, используя группы подстановок. Напомним, что группой подстановок непустого множества  называется подгруппа
называется подгруппа  группы всех подстановок множества
группы всех подстановок множества  . Далее,
. Далее,  называется транзитивной, если для любых
называется транзитивной, если для любых  ,
,  существует такая подстановка
существует такая подстановка  из
из 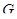 , что
, что  . Напомним, что разбиением множества
. Напомним, что разбиением множества  называется множество
называется множество  попарно непересекающихся подмножеств, объединение которых равно
попарно непересекающихся подмножеств, объединение которых равно  . Тривиальными называются два разбиения, состоящие соответственно из самого
. Тривиальными называются два разбиения, состоящие соответственно из самого  и из всех одноэлементных подмножеств. Транзитивная группа
и из всех одноэлементных подмножеств. Транзитивная группа  подстановок множества
подстановок множества  называется импримитивной, если существует такое нетривиальное разбиение
называется импримитивной, если существует такое нетривиальное разбиение  множества
множества  , что
, что  для всех
для всех  ,
, 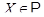 . В противном случае группа называется примитивной. Следующий результат является здесь ключевым.
. В противном случае группа называется примитивной. Следующий результат является здесь ключевым.
Предложение Примитивная группа подстановок  множества
множества  проста, если выполнены следующие условия:
проста, если выполнены следующие условия:
1)  ,
,
2) для некоторого  стабилизатор
стабилизатор  содержит такую нормальную абелеву подгруппу
содержит такую нормальную абелеву подгруппу


