 |
Главная |
Умножение матрицы на число
|
из
5.00
|
Каждый элемент матрицы умножается на это число.
Пример:
 , 0,5
, 0,5  .
.
Сложение матриц
!!! Можно складывать матрицы только одинаковых размеров.
Матрицы складываются поэлементно.
Пример:
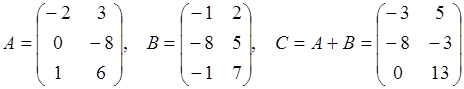 .
.
Вычитание матриц
!!! Можно вычитать матрицы только одинаковых размеров.
Матрицы вычитаются поэлементно.
Пример:
 .
.
Умножение матриц
!!! Матрицу А можно умножить на матрицу В, если число столбцов матрицы А равно числу строк матрицы В.
Произведением матрицы  называется такая матрица
называется такая матрица  , каждый элемент которой cij равен сумме произведений элементов i -ой строки матрицы А на соответствующие элементы j-го столбца матрицы В.
, каждый элемент которой cij равен сумме произведений элементов i -ой строки матрицы А на соответствующие элементы j-го столбца матрицы В.
Возведение в степень
Целой положительной степенью А m ( m >1) квадратной матрицы А называется произведение m матриц равных А, т.е.
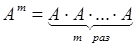 .
.
Пример:
 , найти А2.
, найти А2.
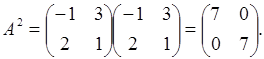
Транспонирование матрицы
Транспонированная матрица – матрица, в которой строки и столбцы поменялись местами с сохранением порядка. Обозначается  .
.
Пример:
 .
.
Обратная матрица
Определение: Матрица  называется обратной по отношению к квадратной матрице А, если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица, т.е.
называется обратной по отношению к квадратной матрице А, если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица, т.е.
 .
.
!!! Обратная матрица существует и единственна тогда и только тогда, когда исходная матрица невырожденная (т.е. определитель матрицы отличен от нуля).
Алгоритм вычисления обратной матрицы:
1. Находим определитель матрицы, т.е.  .
.
2. Находим транспонированную матрицу , т.е.  .
.
3. Находим присоединенную матрицу, т.е  (матрица, состоящая из алгебраических дополнений к элементам транспонированной матрицы).
(матрица, состоящая из алгебраических дополнений к элементам транспонированной матрицы).
4. Вычисляем обратную матрицу по формуле  .
.
5. Проверяем правильность вычисления, исходя из определения обратной матрицы.
Ранг матрицы
Определение: Ранг матрицы – это наивысший порядок, отличных от 0, миноров матрицы.
!!! Чтобы найти ранг матрицы нужно сначала привести матрицу с помощью элементарных преобразований к ступенчатому виду (все элементы, стоящие ниже главной диагонали, равны 0).
Элементарными называются следующие преобразования матриц:
1) умножение всех элементов какой-либо строки (столбца) матрицы на одно и то же число, отличное от нуля;
2) прибавление к элементам какой-либо строки (столбца) матрицы соответствующих элементов другой строки (столбца), умноженных на одно и то же число;
3) перемена местами строк (столбцов) матрицы;
4) отбрасывание строк (столбцов) матрицы, все элементы которых равны нулю.
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
На практике часто сталкиваемся с задачей о сглаживании экспериментальных зависимостей.
Пусть зависимость между двумя переменными x и y выражается в виде таблицы, полученной опытным путем. Это могут быть результаты опыта или наблюдений, статистической обработки материала и т.п.
| xi | x1 | x2 | … | xn |
| yi | y1 | y2 | … | yn |
Требуется наилучшим образом сгладить экспериментальную зависимость между переменными x и y , т.е. по возможности точно отразить общую тенденцию зависимости y от x , исключив при этом случайные отклонения, связанные с неизбежными погрешностями измерений или статистических наблюдений. Такую сглаженную зависимость стремятся представить в виде формулы y = f ( x ) – эмпирическая формула.
Задача нахождения эмпирической формулы разбивается на два этапа:
- устанавливается вид зависимости y = f ( x ), т.е. решить, является ли она линейной, квадратичной, логарифмической или какой-либо другой (в нашей задаче зависимость линейная - y = ax + b );
- определение неизвестных параметров этой функции по методу наименьших квадратов, согласно которому, в качестве неизвестных параметров функции f ( x ) выбирают такие значения, чтобы сумма квадратов отклонений «теоретических» значений f ( xi ), найденных по эмпирической формуле y = f ( x ), от соответствующихопытных значений была минимальной, т.е.

(в нашей задаче  ).
).
В результате решения такой экстремальной задачи с помощью частных производных:
 ,
,
получаем систему нормальных уравнений, из которой находим параметры a и b линейной зависимости:
 .
.
НЕОБХОДИМЫЕ ОПРЕДЕЛЕНИЯ И ФОРМУЛЫ ДЛЯ ВЫЧИСЛЕНИЯ ИНТЕГРАЛОВ
Определение: Функция F ( x ) называется первообразной для функции f ( x ) на промежутке Х, если в каждой точке этого промежутка F ¢ ( x )= f ( x ).
Определение: Совокупность всех первообразных для функции f ( x ) на промежутке Х называется неопределенным интегралом от функции f ( x ) и обозначается  , т.е.
, т.е.
 .
.
Формула Ньютона-Лейбница (для вычисления определенных интегралов):

Формула для вычисления дифференциала функции y = f ( x ):
dy = f ¢ ( x ) dx .
Некоторые свойства неопределенного и определенного интегралов:
Н.и.  , где с – некоторое число,
, где с – некоторое число,
О.и.  , где с – некоторое число;
, где с – некоторое число;
Н.и.  ,
,
О.и.  .
.
!!! Неопределенный интеграл находится приведением интеграла к табличному (сумме табличных) с помощью этих двух свойств или с помощью таких приемов, как методы интегрирования заменой переменных и по частям.
Формула замены переменной в неопределенном интеграле:
 , где
, где  - функция, дифференцируемая на рассматриваемом промежутке.
- функция, дифференцируемая на рассматриваемом промежутке.
Формула замены переменной в определенном интеграле:
 , где
, где  - функция имеет непрерывную производную на отрезке [ a , b ].
- функция имеет непрерывную производную на отрезке [ a , b ].
Формула интегрирования по частям в неопределенном интеграле:
 ,
,
где u = u ( x ), v = v ( x ) – дифференцируемые функции переменной х.
При этом 
Постоянную С в выражении для v в формуле интегрирования по частям полагают равной 0.
Формула интегрирования по частям в определенном интеграле:
 ,
,
где u = u ( x ), v = v ( x ) – функции, имеющие непрерывные производные на отрезке [ a , b ].
Табличные интегралы
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
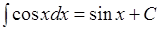 ;
;
 ;
;
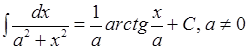 ;
;
 ;
;
 .
.
ОПРЕДЕЛИТЕЛИ
Определение. Пусть дана квадратная матрица второго порядка
 .
.
Определителем (или детерминантом) второго порядка, соответствующим данной матрице, называется число, получаемое по правилу:
 .
.
Определение. Пусть дана квадратная матрица третьего порядка
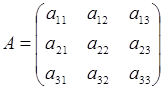 .
.
Определителем (или детерминантом) третьего порядка, соответствующим данной матрице, называют число, получаемое по правилу:


 .
.
Для того, чтобы запомнить, какие произведения в правой части соотношения следует брать со знаком “+”, какие – со знаком “–”, полезно следующее графическое правило, называемое правилом треугольников:
 |  | ||
– со знаком “+”; – со знаком “–”.
ПРЕДЕЛЫ
Основные понятия и определения
Определение: Функция  называется бесконечно малой величиной (БМВ) при
называется бесконечно малой величиной (БМВ) при  или при
или при  , если ее предел равен нулю:
, если ее предел равен нулю:
 .
.
Свойства бесконечно малых величин:
- алгебраическая сумма конечного числа бесконечно малых величин есть величина бесконечно малая;
- произведение БМВ на ограниченную функцию есть БМВ;
- частное от деления БМВ на функцию, предел которой отличен от 0, есть БМВ.
Определение: Функция 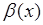 называется бесконечно большой величиной (ББВ) при
называется бесконечно большой величиной (ББВ) при 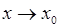 или при
или при  , если ее предел равен бесконечности.
, если ее предел равен бесконечности.
!!! Если  - БМВ при
- БМВ при 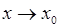 или при
или при  , то функция
, то функция 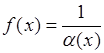 является ББВ при
является ББВ при  или при
или при  . Верно и обратное утверждение.
. Верно и обратное утверждение.
Свойства бесконечно больших величин:
- сумма ББВ и ограниченной функции, есть ББВ;
- произведение ББВ на функцию, предел которой отличен от 0 есть ББВ;
- частное от деления ББВ на функцию, имеющую предел, есть ББВ.
|
из
5.00
|
Обсуждение в статье: Умножение матрицы на число |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

