ТЕОРЕТИЧЕСКИЕ ОСНОВЫ АЛГОРИТМИЗАЦИИ И

ПРОГРАММИРОВАНИЯ

Основные понятия алгоритмизации

    «Многие не сведущие в математике люди думают, что поскольку назначение аналитической машины Бэббиджа – выдавать результаты в численном виде, то природа происходящих в ней процессов должна быть арифметической и численной, а не алгебраической и аналитической.

    Но они ошибаются. Машина может упорядочивать и комбинировать числовые значения так же, как и буквы или любые другие символы общего характера.

    В сущности, при выполнении соответствующих условий она могла бы выдавать результаты и в алгебраическом виде».

Августа Ада, графиня Лавлейс (1844)

    Основоположницей программирования считают Августу Аду – дочь великого английского поэта Дж. Г. Байрона. В 19 веке в Англии впервые появилось настоящее арифметическое устройство – аналитическая машина Бэббиджа: с регистрами, сумматором и другими атрибутами, присущими процессору современного компьютера. Программы для такого устройства расписывались на бумаге. Каждая операция совершалась поворотом особой ручки или нажатием рычага такой машины. Большинство идей и принципов программирования для аналитической машины Бэббиджа было рассмотрено в книге Августы Ады^* «Комментарии». Позднее появился особый вид деятельности – программирование, а в последствии возникла профессия программиста.

    Понятие «алгоритм» является основным для всей области компьютерного программирования, поэтому начать мы должны с тщательного анализа этого термина. Слово «алгоритм» (англ. algorithm) уже само по себе представляет большой интерес.

Историки-математики обнаружили истинное происхождение этого слова: оно берет начало от имени автора знаменитого персидского учебника по математике, Абу Абд Аллах Мухаммед ибн Муса аль-Хорезми (ок. 825 г.). Аль-Хорезми написал знаменитую книгу «Книга о восстановлении и противопоставлении» (перс. Китаб аль-джебр валь-мукабала). От названия этой книги, которая была посвящена решению линейных и квадратных уравнений, произошло еще одно слово – «алгебра».

В старинном немецком математическом словаре Vollstandiges mathematisches Lexicon (Лейпциг, 1747) дается следующее толкосание латинского слова algorithmus : «Этот термин включает в себя понятие о четырех типах арифметических операций, а именно: о сложении, умножении, вычитании и делении». Латинское выражение algorithmus infinitesimalis в то время использовалось для определения способов выполнения действий с бесконечно малыми величинами, открытых великим математиком Лейбницем.

Пример 1-1. Алгоритм Евклида.

Приблизительно через 100 лет после появления аналитической машины Бэббиджа была создана первая электронная вычислительная машина – специально для выполнения атомного проекта в Лос-Аламосе (США). В это время (конец 40-х – начало 50-х годов 19 века) слово «алгоритм» чаще всего ассоциировалось с алгоритмом Евклида, который представляет собой процесс нахождения наибольшего общего делителя двух чисел. Этот алгоритм далее будем называть «алгоритмом Е».

Сущность алгоритма Е: даны два целых положительных числа т и п. Требуется найти их наибольший общий делитель, т.е. наибольшее целое положительное число, которое нацело делит оба числа т и п. Алгоритм состоит из трех элементарных типовых действий: Е1, Е2 и Е3 (рис. 1.1).

Действие Е1. Нахождение остатка.

Разделим m на п, и пусть остаток от деления будет равен r,где .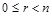

Действие Е2. Сравнение с нулем.

Если r = 0, то выполнение алгоритма прекращается; п – это искомое значение.

Действие Е3. Замещение.

Присвоить m n, n r и вернуться к шагу E1. ô

Разумеется, у Евклида этот алгоритм сформулирован не совсем так. Приведенная выше формулировка иллюстрирует стиль, в котором алгоритмы будут представлены на протяжении всей этой книги.

Каждому рассматриваемому алгоритму присваивается идентифицирующая буква (в предыдущем примере использовалась буква Е), а шагам алгоритма – эта же буква в сочетании с числом (El, Е2, ЕЗ).

Каждый шаг любого алгоритма, например Е1 в вышеприведенном алгоритме, начинается фразой, которая как можно более кратко выражает содержание данного шага. Обычно эта фраза отражается также в сопровождающей алгоритм блок-схеме, такой как на рис. 1.1, чтобы читатель мог легко представить себе описанный алгоритм.

За краткой фразой следует формулировка (выраженная с помощью слов и символов) действия, которое нужно выполнить, или решения, которое нужно принять. Могут присутствовать также заключенные в круглые 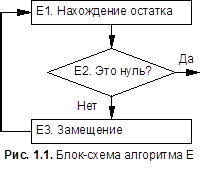скобки комментарии. Комментарии играют роль пояснений к шагу; с их помощью часто указываются некоторые постоянные характеристики переменных или текущие цели данного этапа. В комментариях не определяются действия, которые являются составной частью алгоритма; они служат только для удобства читателя, чтобы по возможности помочь ему разобраться в алгоритме.

Стрелка «», используемая на шаге ЕЗ, обозначает важнейшую операцию замещения, которую иногда называют присвоением или подстановкой: запись m n указывает, что значение переменной т замещается текущим значением переменной п. В начале работы алгоритма Е, т и п – это заданные первоначальные значения, но по окончании его работы эти переменные будут иметь, вообще говоря, совершенно другие значения.

Стрелка используется для того, чтобы отличать операцию замещения от отношения равенства. Мы не будем говорить: «Установим т = п», а, вероятно, спросим: «Действительно ли т = п?». Знак «=» обозначает условие, которое можно проверить, а знак «» – действие, которое можно выполнить. Операция увеличение п на единицу обозначается через п п+1 и читается так: «п замещается значением п+1» или «п принимает значение п+1». Вообще говоря, запись «переменная формула» означает, что формула будет вычислена на основании текущих значений всех входящих в нее переменных, а полученный результат будет присвоен переменной, стоящей слева от стрелки (таким образом, вычисленный по формуле результат заменит собой предыдущее значение переменной слева). Лица, не имеющие достаточного опыта программирования, иногда говорят, что «п переходит в п+1» и для обозначения операции увеличения п на единицу используют запись п ® п+1. Такая система обозначений и формулировок противоречит стандартным соглашениям и может привести только к путанице, поэтому ее следует избегать.

Обратите внимание, что на шаге ЕЗ очень важен порядок действий. Действительно, две записи:

1) «присвоить m n, n r »

и

2) «присвоить n r, m n »

– это совсем не одно и то же.

Из второй записи следует, что предыдущее значение n будет потеряно до того, как его смогут присвоить т. На самом деле эквивалентом второй записи будет «присвоить n r, т r ». Когда нескольким переменным присваивается одно и то же значение, в одном выражении можно использовать несколько стрелок. Так, например, операцию « n r, т r » можно записать как « n т r ».

Операцию взаимного обмена значениями двух переменных можно записать так: «Обмен т « n». Ее можно записать и с помощью новой переменной t следующим образом: "Присвоить t т, т п, п t .

Выполнение алгоритма начинается с шага, имеющего наименьший номер (обычно это шаг 1). Затем последовательно выполняются следующие шаги, если нет каких-либо указаний, нарушающих естественный порядок выполнения. На шаге ЕЗ указание «Вернуться к шагу Е1» явным образом определяет порядок вычислений. На шаге Е2 действию предшествует условие «Если r = 0» и если r #0, то оставшаяся часть предложения не применяется и нет указаний на выполнение в этом случае каких-либо действий. Конечно, мы могли бы добавить дополнительное предложение «Если r #0, то перейти к шагу ЕЗ», но это совершенно излишне.

Жирная вертикальная черточка «ô», помещенная в конце шага ЕЗ, обозначает окончание алгоритма и продолжение текста.

Итак, мы обсудили практически все соглашения об обозначениях, которые используются в алгоритмах, приведенных в книге. Осталось выяснить только, как обозначать величины с индексами (или «подстрочными» индексами), которые являются элементами упорядоченного массива. Предположим, у нас есть п величин: v₁, v₂, …, v_n . Для обозначения j-гоэлемента вместо записи v_j часто используется запись v[j]. Аналогично массив иногда предпочитают обозначать как а[i, j], вместо того чтобы использовать два подстрочных индекса, как в записи a_ij. Иногда для обозначения переменных используются имена, состоящие из нескольких букв, обычно прописных. Например, TEMP может быть именем переменной, использующейся для временного хранения вычисленного значения, a PRIME [К] может обозначать k-е простое число, и т.д.

До сих пор мы говорили о форме записи алгоритмов, а теперь давайте попробуем выполнить один из них. Хочу сразу заметить, что читателю не следует рассчитывать на то, что алгоритмы можно читать, как роман. Такое чтение приведет к тому, что вам будет трудно понять, что же на самом деле происходит при выполнении алгоритма. Чтобы проверить алгоритм, в нем нужно разобраться, и лучший способ понять, как он работает, – испытать его. Поэтому нужно взять карандаш и бумагу и прорабатывать от начала до конца каждый алгоритм сразу же, как только он встретится в тексте. Обычно к примеру алгоритма прилагается схема, в противном случае читатель легко сможет представить ее. Это самый простой и доступный способ разобраться в алгоритме, в то время как все остальные подходы оказываются неэффективными.

Итак, давайте в качестве примера разберем алгоритм Е. Предположим, что m = 119 и n = 544.

Начнем с шага Е1. Деление m на n в этом случае выполняется просто, даже очень просто, так как частное равно нулю, а остаток – это 119. Таким образом, r 119. Переходим к шагу Е2. Поскольку r #0, на этом шаге никакие действия не выполняются.

На шаге ЕЗ присваиваем т 544, п 119. Очевидно, что если первоначально m < п, то частное на шаге Е1 всегда оказывается равным нулю и в ходе выполнения алгоритма всегда происходит взаимный обмен значений переменных тип, хотя и таким громоздким способом. Поэтому можно добавить дополнительный шаг:

Действие Е0.Гарантировать, что m > п.

Если m < п, то выполнить взаимный обмен т « n.

В результате алгоритм изменится незначительно (разве что увеличится на один шаг), но зато время его выполнения сократится примерно в половине случаев.

Вернемся к шагу Е1. Находим, что

.

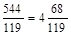Поэтому r 68. В результате на шаге Е2 снова не выполняются никакие действия, а на шаге ЕЗ присваиваем т 119, п 68.

В следующих циклах сначала получаем r 51 и т 68, п 51, а затем: r 17 и т 51, п 17.

Наконец, в результате деления 51 на 17 получаем: r 0. Таким образом, на шаге Е2 выполнение алгоритма прекращается. Наибольший общий делитель 119 и 544 равен 17.

Вот что такое алгоритм.