 |
Главная |
Математическая индукция
|
из
5.00
|
Математические методы, используемые при анализе алгоритмов, имеют свои отличительные особенности. Например, нам довольно часто придется выполнять суммирование конечного числа рациональных чисел или решать рекуррентные уравнения. Подобные темы обычно очень поверхностно освещаются при чтении математических дисциплин, поэтому назначение следующих разделов – не только потренироваться в использовании обозначений, но и проиллюстрировать типы и методы вычислений, которые будут нам особенно необходимы.
Пусть Р(п)– это некоторое утверждение, касающееся целого числа п,например:
«n умножить на (n + 3) – четное число» или «если п ³ 10, то 2n > n3». Предположим, нам нужно доказать, что утверждение Р(п) верно для всех положительных целых чисел п. Существует важный метод доказательства этого факта, который состоит в следующем:
(а) Доказать, что Р(1) верно.
(b) Доказать, что «если Р(1), Р(2), ..., Р(п)справедливы, то Р(п+1) также справедливо»; это доказательство должно иметь силу для любого целого положительного числа п.
Пример 1-2.Нечетные числа в сумме дают квадрат.
В качестве примера рассмотрим следующие известные с древних времен равенства, которые многие исследователи открывали независимо друг от друга:
| 1 = 12, | ||
| 1 + 3 = 22, | ||
| 1 + 3 + 5 = 32, | (1.4) | |
| 1 + 3 + 5 + 7=42, | ||
| 1 + 3 + 5 + 7 + 9 = 52. |
В общем виде эти равенства можно записать следующим образом:
1 + 3 + ××× + (2n – 1) = n2 . (1.5)
Обозначим это утверждение как Р(п)и докажем, что оно верно для любого положительного n. Согласно методу, описанному выше, имеем следующее.
(а) «Р(1) верно, так как 1 = 12 »
(b) «Если все утверждения Р(1), ..., Р(п) справедливы, то, в частности, верно и Р(п); следовательно, выполняется соотношение (1.5). Добавляя к обеим частям этого уравнения 2п + 1, получаем:
1 + 3 + ××× + (2п - 1) + (2п + 1) = п 2 + 2 п + 1 = (п + 1)2.
Таким образом, утверждение Р(п + 1) также справедливо».
Этот метод можно считать алгоритмической процедурой доказательства. В самом деле, следующий алгоритм дает доказательство утверждения Р(п) для любого целого положительного п в предположении, что этапы нашего доказательства (а) и (b) уже выполнены.
 Алгоритм I (Построить доказательство). Для заданного целого положительного числа n этот алгоритм
Алгоритм I (Построить доказательство). Для заданного целого положительного числа n этот алгоритм
(рис. 1.2) выдаст доказательство того, что утверждение Р(п)верно.
Действие I 1. Доказать Р(1).
Присвоить k 1 и в соответствии с п. (а) выдать доказательство утверждения Р(1).
Действие I 2. k = n ?
Если k = n, закончить выполнение алгоритма; требуемое доказательство выдано.
Действие I 3. Доказать P(k + 1).
Согласно п. (b) выдать доказательство того, что «Если все утверждения Р(1), ..., P(k)справедливы, то P(k + 1) также справедливо». Вывести фразу «Мы уже доказали, что если утверждения Р(1), ..., P(k)верны, то верно и P(k+1)».
Действие I 4. Увеличить k . Увеличить k на 1 и перейти к шагу I 2. ô Поскольку этот алгоритм выдает доказательство утверждения Р(п) для любого заданного п, метод доказательства, сформулированный в пп. (а) и (b), логически обоснован. Он называется доказательством методом математической индукции.
Понятие математической индукции следует отличать от того, что в научной практике обычно называют индуктивным методом. Данный метод заключается в том, что ученый делает некоторые наблюдения и создает «по индукции» общую теорию или выдвигает гипотезу, объясняющую эти факты. Например, на основании пяти соотношений (1.4), приведенных выше, мы могли бы сформулировать соотношение (1.5). В этом смысле индукция – не более чем догадка или попытка объяснить конкретную ситуацию; математики называют это эмпирическим результатом или предположением.
Для того чтобы прояснить суть дела, рассмотрим еще один поучительный пример. Пусть р(п)обозначает количество разбиений числа п, т.е. количество различных способов записи числа п в виде суммы целых положительных чисел (порядок слагаемых значения не имеет). Так как для числа 5 существует ровно семь таких способов записи, т.е.
1 + 1 + 1 + 1 + 1 = 2 + 1 + 1 + 1 = 2 + 2 + 1 = 3 + 1 + 1 = 3 + 2 = 4 + 1 = 5 ,
то р(5) = 7. На самом деле установить первые пять значений функции р(п) довольно легко:
р(1) = 1, р(2) = 2, р(3)=3, р(4) = 5, р(5) = 7.
Замечание. На этом основании мы могли бы предварительно сформулировать по индукции некорректное предположение о том, что последовательность р(2), р(3), ...пробегает множество простых чисел. Для проверки данной гипотезы продолжаем вычисления и находим р(6) = 11. – Ура! – Это подтверждает наше предположение. Но, к сожалению, оказывается, что р(7)равно 15. Увы, все идет насмарку, и приходится начинать сначала. Из математической литературы известно, что значения р(n) отличаются довольно сложным поведением.
Математическая индукция не имеет ничего общего с тем индуктивным методом, который мы только что описали. «Индукцией» этот метод назван только потому, что сначала нужно выдвинуть предположение о том, что нужно доказать, а затем уже применять метод математической индукции. Начиная с этого момента, слово «индукция» будет использоваться только для обозначения доказательства методом математической индукции.
Есть еще одно доказательство соотношения (1.5). На рис. 1.3 для п = 6 показано, что п2 клеток разбиты на группы 1 + 3 + (2n – 1) клеток. Но, в конечном счете, этот рисунок можно считать «доказательством» только в случае, если мы покажем, что данное построение можно выполнить для любого п. А это, в сущности, и будет доказательством по индукции.
 В нашем доказательстве соотношения (1.5) был использован только частный случай (b); мы просто показали, что из справедливости Р(п)следует справедливость Р(п+1). Это очень важный случай, который встречается довольно часто, но в следующем примере будут проиллюстрированы более широкие возможности метода математической индукции.
В нашем доказательстве соотношения (1.5) был использован только частный случай (b); мы просто показали, что из справедливости Р(п)следует справедливость Р(п+1). Это очень важный случай, который встречается довольно часто, но в следующем примере будут проиллюстрированы более широкие возможности метода математической индукции.
Пример 1-3.Числа Фибоначчи.
Определим последовательность Фибоначчи F0, F1, F2, ..., F2 с помощью такого правила: F0 = 0, F1 = 1, а каждый последующий член равен сумме двух предыдущих. Таким образом, первые члены этой последовательности выглядят так: 0, 1, 1, 2, 3, 5, 8, 13, ... . Далее введем обозначение:
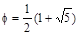 . (1.6)
. (1.6)
Докажем, что неравенство  справедливо для всех целых положительных чисел n. Назовем эту формулу утверждением P(n).
справедливо для всех целых положительных чисел n. Назовем эту формулу утверждением P(n).
Если n = 1, то F1 = 1 = f0 = f n – 1 ,поэтому п. (а) выполнен.
Переходя к п. (б), заметим сначала, что Р(2) также справедливо, поскольку F1= 1 < 1.6 < f1= f 2 – 1. А теперь, если все Р(1), Р(2), ..., Р(п)справедливы и п > 1, то мы знаем, в частности, что справедливы Р(п – 1) и Р(п). Поэтому  и
и 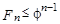 . Складывая данные неравенства, получаем:
. Складывая данные неравенства, получаем:
 . (1.7)
. (1.7)
Важное свойство числа ф, которое и является причиной первоочередного выбора этого числа для данной задачи, состоит в том, что
1 + f = f2. (1.8)
Подставив (1.8) в (1.7), получим  ,а это и есть утверждение Р(п+1). Таким образом, п. (b) выполнен, и формула (1.6) доказана методом математической индукции. Обратите внимание, что п. (b) мы выполняли двумя различными способами: непосредственно доказали Р(п + 1) при п=1 и использовали индуктивный метод при п > 1. Это было необходимо, так как при п=1ссылка на Р(п – 1) = Р(0)была бы незаконной.
,а это и есть утверждение Р(п+1). Таким образом, п. (b) выполнен, и формула (1.6) доказана методом математической индукции. Обратите внимание, что п. (b) мы выполняли двумя различными способами: непосредственно доказали Р(п + 1) при п=1 и использовали индуктивный метод при п > 1. Это было необходимо, так как при п=1ссылка на Р(п – 1) = Р(0)была бы незаконной.
|
из
5.00
|
Обсуждение в статье: Математическая индукция |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

