Модели неевклидовой геометрии

Доказать непротиворечивость новой геометрии ни Лобачевский, ни Бойяи не сумели — тогда математика ещё не располагала необходимыми для этого средствами. Только спустя 40 лет появились модель Клейна (1871) и модель Пуанкаре (1882), реализующие аксиоматику геометрии Лобачевского на базе евклидовой геометрии. Эти модели убедительно доказывают, что отрицание V постулата не противоречит остальным аксиомам геометрии; отсюда вытекает, что V постулат независим от остальных аксиом и доказать его невозможно.

8. ПОНЯТИЕ МНОЖЕСТВА, ПАРАМЕТРЫ.

Множество — одно из первоначальных понятий в математике, не подлежащих определению. Как правило, множества задаются определенным свойством. Всякий предмет (объект) принадлежит множеству тогда и только тогда, когда он обладает данным свойством.

Применение в математике

Предметы (объекты), которые составляют множество, называют его элементами. Для обозначения множества обычно используют большие буквы (A, B, X), при этом запись A = {a, b, c, …} означает, что множество A состоит из элементов a, b, c, ….

Чтобы записать утверждение «элемент a принадлежит множеству A», используют обозначение a A. Аналогично, утверждение «элемент a не принадлежит множеству A» записывается как a ∉ A.

Множество называется конечным, если оно состоит из конечного числа элементов. В противном случае множество называется бесконечным. Существует также пустое множество, которое вообще не содержит элементов, оно обозначается символом ∅.

Множество A называется подмножеством B, если выполнено условие: или . Таким образом,

Понятие равенства множеств

Множества А и В равны (A = B), если одновременно выполнены два утверждения:  .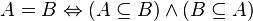

Наиболее часто встречающиеся множества имеют стандартные обозначения в математике:

§ N — множество всех натуральных чисел

§ Z — множество всех целых чисел

§ Q — множество всех рациональных чисел

§ R — множество всех действительных чисел

§ C — множество всех комплексных чисел

9. ОПРЕДЕЛЕНИЕ ПОДМНОЖЕСТВ И ПУСТОГО МНОЖЕСТВА.

Мно́жество — один из ключевых объектов математики, в частности, теории множеств и логики.

Понятие множества обычно принимается за одно из исходных (аксиоматических) понятий, то есть не сводимое к другим понятиям, а значит и не имеющее определения.

Определения

· Множество A является подмножеством множества B, если любой элемент, принадлежащий A, также принадлежит B. Пишут: или . Таким образом,

· Множество B в таком случае называется надмно́жеством множества A, и этот факт часто записывают: или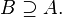

Множество A называется подмножеством множества B, если все элементы A являются также элементами B. Любое множество является своим подмножеством: Если при этом , то A называется собственным подмножеством B. По определению полагают, что пустое множество является подмножеством любого множества: .

Множество всех подмножеств множества A обозначается или 2^A, так как оно соответствует множеству отображений из A в 2 = {0,1}. Иногда его называют множеством-степенью (англ. power set) для A. Мощность множества-степени, по теореме Кантора, всегда больше, чем у исходного множества. В категории множеств — это контравариантный функтор, отображающий функцию 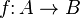в при этом отображение 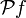ставит в соответствие каждому подмножеству B его полный прообраз в A.

Примеры:

· Подмножествами множества {0,1,2,3,4,5} являются множества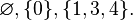

· Подмножествами множества являются множества

· Пусть A = {a,b}, тогда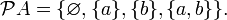

[править] Собственное подмножество

Из определения прямо следует, что пустое множество обязано быть подмножеством любого множества. Также, очевидно, любое множество является своим подмножеством:

.

Если , и , , то A называется со́бственным или нетривиа́льным подмножеством.

[править] Свойства

Отношение подмножества обладает целым рядом свойств.^[1]

· Отношение подмножества рефлексивно:

· Отношение подмножества антисимметрично:

· Отношение подмножества транзитивно:

· Пустое множество является подмножеством любого другого:

· Таким образом отношение подмножества является отношением частичного порядка на булеане 2^M — семействе всех подмножеств любого объемлющего множества M.

· Для любых двух множеств A и B следующие утверждения эквивалентны:

·

·

·

·

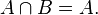
10. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ