Генераторы случайных последовательностей

Введение

Среди способов защиты информации наиболее важным считается криптографический. Он предусматривает такое преобразование информации, при котором она становится доступной для прочтения лишь обладателю некоторого секретного параметра (ключа). В последние годы область применения криптографии значительно расширилась. Ее стали повседневно использовать многие организации, коммерческие фирмы, частные лица. При этом законного пользователя того или иного криптографического средства, прежде всего беспокоит его надежность. Одним из способов оценки надежности является попытка «взлома», т.е. получение доступа к информации без знания ключа. Подобные задачи призвано решать смежное научное направление, называемое криптоанализом. Криптоанализ и криптография объединены общим названием – криптология.

Вводная лекция.

Защита информации – это всевозможные средства и функции, обеспечивающие доступность, конфиденциальность или целостность информации или связи, исключая средства и функции, предохраняющие от неисправностей. Защита информации включает в себя криптографию, криптоанализ, защиту от собственного излучения и защиту (компьютера) от несанкционированного доступа.

Криптография – это раздел прикладной математики, изучающий модели, методы, алгоритмы, программные и аппаратные средства преобразования информации (шифрования) в целях сокрытия ее содержания, предотвращения видоизменения или несанкционированного использования.

Криптосистема – это система, реализованная программно, аппаратно или программно-аппаратно и осуществляющая криптографическое преобразование информации.

Криптоанализ – это раздел прикладной математики, изучающей модели, методы, алгоритмы, программные и аппаратные средства анализа криптосистемы или ее входных и выходных сигналов с целью извлечения конфиденциальных параметров, включая открытый текст.

Из данных определений видно, что криптоанализ занимается задачами, которые в математическом смысле обратные задачи криптографии. Система криптографии и криптоанализа образует новую науку – криптологию.

В развитии криптологии принято выделять три этапа.

Первый этап. (С древних времен до 1949г). Этот этап характеризуется частными, узкоспециальными и вычислительно простыми алгоритмами криптографии и криптоанализа без использования компьютеров. Его часто называют этапом до компьютерной криптографии.

Второй этап. (1949-1976гг.) Этот этап принято отсчитывать с момента публикации американского математика-прикладника К. Шеннона «Теория связи в секретных системах». В этот период принято активно проводились систематические исследования по криптологии с использованием компьютера. Криптология становится математической наукой.

Третий этап. (1976г. – настоящее время). Этот этап можно назвать и «эрой открытой криптологии». Этот этап принято отсчитывать с момента публикации работы американских математиков У.Дифори, М.Хеллмана «Новые направления в криптографии».В этой работе было показано, что «секретная» передача информации возможна (вотличие от результатов Шеннона) без предварительной передачи «секретного ключа».

Главной особенностью этого этапа становится массовое применение криптографии в банковском деле, электронной торговле, компьютерных сетях и других сферах жизнедеятельности.

Современная криптология широко использует теорию вероятностей, математическую статистику, алгебру, теорию чисел и теорию алгоритмов.

Некоторые определения и формулы.

В криптологии общеприняты следующие понятия:

· Пространство сообщений 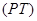 – множество всевозможных сообщений 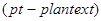. Для сообщений используется также обозначение .

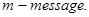· Пространство ключей 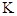. Каждый ключ к 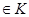определяет некоторую подстановку  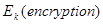на пространство 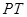и обратное преобразование .

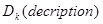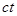
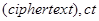
· Пространство зашифрованных сообщений , состоящее из зашифрованных 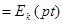. Используется также обозначение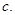

Остается уточнить понятие текста. При этом обычно фиксируют некоторую сумму символов, называемую алфавита. Это может быть английский, русский или какой-нибудь другой алфавит. Часто в качестве алфавита используются натуральные числа или символы 0 и 1. Словом называется упорядоченный набор букв данного алфавита. Множество слов обозначают через 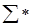. Текст набор слов.

Арифметические основы

Основные обозначения.

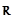- множество вещественных (действительных) чисел. Вещественное число – любое положительное число, отрицательное число, или нуль.

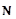- множество натуральных чисел.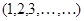

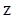- множество целых чисел.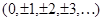  

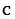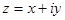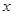- множество комплексных чисел. Комплексное число – число вида , где и 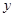 - действительные числа, а - т.н. мнимая единица, т.е. число, квадрат которого равен -1.

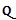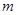- множество рациональных чисел. Рациональное число – число, которое может быть представлено в виде дроби , где и 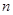- целые числа ( ).

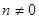Простые числа. Натуральное число 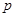> 1 называется простым, если оно не имеет других натуральных делителей, кроме 1 и 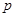. Простым числом будет наименьший, отличный от единицы делитель целого числа 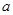, 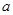>1. Простых чисел бесконечно много.

Взаимно простые числа. Два целых числа 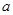и 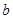будут взаимно простыми тогда и только тогда, когда найдутся  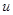и 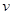, такие что .

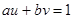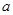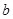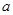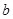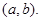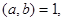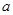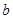Наибольший общий делитель. Всякое целое, делящее числа и , называется их общим делителем. Наибольший из общих делителей для чисел и называется наибольшим общим делителем (НОД) и обозначается  Ввиду конечности числа делителей одного числа существование и единственность наибольшего общего делителя очевидны. Если то числа  и  называются взаимно простыми.

Алгоритм Евклида. Способ нахождения наибольшего общего делителя двух целых Для случая положительных чисел 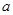и 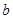, причем  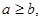этот способ состоит в следующем. Деление с остатком числа 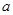на число 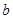приводит к результату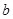 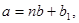где частное  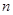является целым положительным числом, а остаток 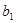- либо 0, либо положительное число, меньше 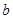, 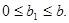Производится последовательное деление:

 

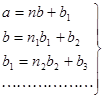 (2.1)

 

(где все 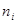-положительные целые числа и 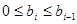) до тех пор, пока не получится остаток, равный 0. Этот последний остаток  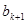можно не писать, так что ряд равенств (2.1) закончится следующим образом:

 

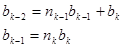 (2.2)

 

Последний положительный остаток 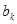 в этом процессе и является наибольшим общим делителем чисел 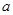и .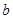

/Пример/

 

Найдем НОД (175,77).

175=77*2+21;

77=21*3+14;

21=14*1+7;

14-7*2.

 

Последний положительный остаток равен 7. Следовательно (175,77)=7.

Наименьшее общее кратное. Всякое целое, кратное всех данных чисел, называется их общим кратным. Наименьшее положительное общее кратное называется наименьшим общим кратным (НОК) и обозначается .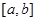

Классы вычетов. Числа, сравнимые по модулю , образуют классвычетов по модулю . Все числа из одного класса имеют один и тот же остаток 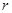 от деления на . Любое число 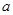из класса вычетов называется вычетом по модулю .Соответствующий класс обозначается через 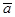. Поскольку соотношение 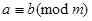является бинарным отношением эквивалентности, то имеем разбиение целых чисел на классы эквивалентности (классы вычетов). Всего имеется  классов вычетов по модулю : .

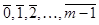Функция Эйлера. Арифметическая функция 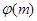, значение которой равно количеству положительных целых чисел, не превосходящих  и взаимно простых с .

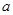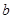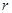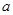Сравнения. Мы будем рассматривать целые числа в связи с остатками от деления их на данное целое положительное число . Каждому целому числу отвечает определенный остаток от деления его на ; если двум целым и  отвечает один и тот же остаток , то они называются равностаточными по модулю  или сравнимыми по модулю . Сравнимость чисел и 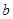 по модулю  записывается так:

 

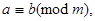 (2.3)

 

это читается следующим образом: 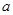сравнимо с  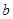по модулю .

*Доказательство*

 

Из 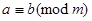 следует, что

 

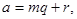
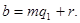
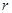( - остаток от деления 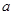на 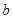,  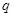- неполное частное)

откуда

 

 

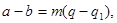
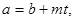
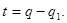
Обратно, из 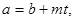 представляя  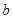в виде

 

 

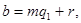
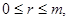
выводим

 

 

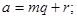
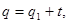
т.е.

 

. □

 

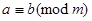Сравнимость чисел 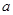и 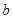 по модулю  равносильна: возможности представить 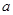 в ви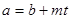де , где 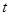 - целое.

Свойства сравнений.

1. Два числа, сравнимые с третьим, сравнимы между собой.

2. Сравнения можно почленно складывать.

3. Слагаемое, стоящее в какой-либо части сравнения, можно переносить в другую часть, переменив знак на обратный.

4. Сравнения можно почленно перемножать.

5. Обе части сравнения можно возвести в одну и ту же степень.

6. Обе части сравнения можно умножить на одно и то же целое число.

7. Обе части сравнения можно разделить на их общий делитель, если последний взаимно прост с модулем.

8. Обе части сравнения и модуль можно умножить на одно и то же целое.

9. Обе части сравнения и модуль можно разделить любой их общий делитель.

10. Если сравнение 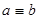 имеет место по нескольким модулям, то оно имеет место и по модулю, равному общему наименьшему кратному этих модулей.

11. Если сравнение имеет место по модулю , то оно имеет место и по модулю 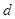, равному любому делителю числа .

12. Если одна часть сравнения и модуль делятся на какое-либо число, то и другая часть сравнения должна делиться на то же число.

Первообразные корни. При 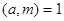 существуют положительные  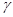с условием 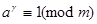, например (теорема Эйлера) 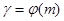.Наименьшее из них называется: показатель, которому  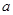принадлежит по модулю .

    Если 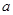 по модулю  принадлежит показателю 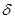, то числа  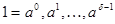по модулю  несравнимы.

    Если 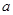 по модулю  принадлежит показателю 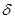, то 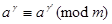 тогда и только тогда, когда  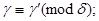в частности (при 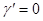), , 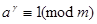тогда и только тогда, когда  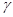делится на .

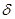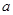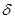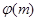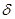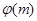    Пусть  по модулю  принадлежит показателю . Тогда  делится на . Таким образом, показатели, которым числа принадлежат по модулю , есть делители . Числа, принадлежащие показателю  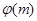(если такие существуют), называются первообразными корнями по модулю .

Символ Лежандра. Функция чисел 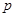и 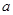, определенная для простых нечетных 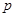и целых 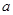, не делящихся на 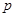называется символом Лежандра и обозначается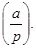

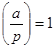, если сравнение  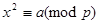разрешимо, в противном случае же случае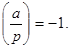

Символ Якоби. Символ Якоби является обобщением символа Лежандра и служит для упрощения вычисления последнего. Пусть 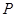 - нечетное натуральное число,  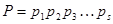- его разложение на простые множители. Для всякого целого 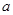, , 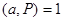символ Якоби определяется по формуле:

 

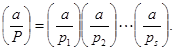
Цепные дроби. Цепная дробь – один из важнейших способов представления чисел и функций. Цепная дробь есть выражение вида

 

 

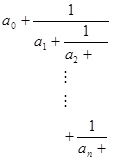
где 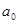- любое целое число,  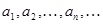- натуральные числа, называемые неполными частными.

Алгебраические основы

Понятие группы.

Группой называется непустое множество 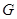 с алгебраической операцией * на нём, для которой выполняется первые 3 из четырёх следующих аксиом.

1). Операция * ассоциативна, т.е. для любых .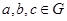

 

 

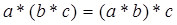
2). В G имеется единичный элемент (или единица) e такой, что для любого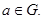

 

 

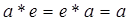
3). Для каждого a Î G существует обратный элемент 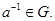 такой, что

 

 

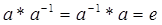
4). Для любых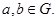

 

 

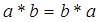
Если дополнительно группа удовлетворяет четвертой аксиоме, то группа называется абелевой или коммутативной.

Множество 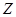 образует группу относительно операции сложения. То же можно сказать относительно рациональных чисел 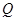, вещественных чисел  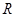и комплексных чисел .

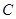Через 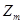 будет отличать аддитивную группу классов вычетов по модулю m.

Если взять все классы вычетов, взаимно простые с модулем m, и определить их умножение по модулю m, то получится группа, обозначаемая через 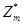. Число элементов конечной группы  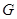называется порядком группы и обозначается через .

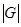Группа 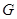 называется циклической, если она порождена одним элементом, т.е. в ней имеется такой элемент a, что любой другой элемент представим в виде 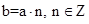. Если  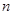– отрицательное, то под  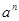понимается произведение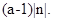

Циклическими являются группы 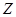 и 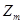. Группа 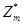– циклическая лишь в случае, когда по модулю m существует первообразный корень.

Циклическая группа всегда коммутативна.

Подгруппы групп.

Подмножество 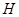 группы  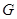называется подгруппой этой группы, если H образует группу относительно операции группы .

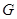Подгруппы группы 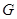, отличные от тривиальных групп 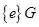, называется собственными подгруппами.

Гамоморфизмы групп.

Отображение 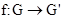 группы  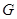в группу  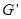называется гомоморфизмом, если оно согласовано с операциями на группах  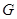и 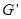, т.е.  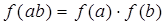для любых элементов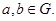

Кольца и поля.

Кольцом называется множество 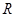 с двумя бинарными операциями, обозначаемыми символами “+” и “*”, такими что:

1). 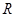 – абелева группа;

2). Операция умножения ассоциативна, т.е. для всех ;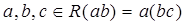

3). Выполняются законы дистрибутивности, т.е. для всех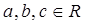

 

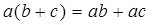 и ;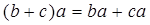

Подкольца.

Подмножество 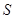 кольца  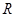называется подкольцом этого кольца, если оно замкнуто относительно имеющихся операций сложения и умножения и само образует кольцо относительно этих операций.

Гомоморфизмы колец.

Пусть 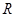 и 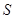 – кольца. Гомоморфизмом  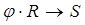называется отображение, для которого 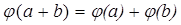, , 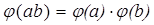 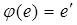при всех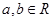

 

Генераторы случайных последовательностей