 |
Главная |
Электронная подпись (цифровая подпись).
|
из
5.00
|
Если 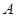 планирует подписывать документ Ц.П., то он должен выбрать параметры RSA.
планирует подписывать документ Ц.П., то он должен выбрать параметры RSA. 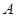 выбирает два простых числа
выбирает два простых числа 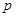 и
и 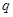 , вычисляет
, вычисляет 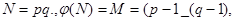 затем выбирает число
затем выбирает число 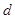 ,взаимно простое с
,взаимно простое с 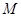 , и вычисляет
, и вычисляет 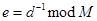 , далее публикует числа
, далее публикует числа 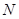 и
и 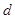 и хранит в секрете
и хранит в секрете 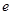 . Числа
. Числа 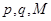 – более не понадобятся.
– более не понадобятся.
Пусть 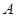 хочет подписать сообщение
хочет подписать сообщение 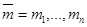 . Тогда
. Тогда 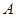 вычисляет хеш-функцию
вычисляет хеш-функцию 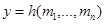 , которая ставит в соответствие сообщению
, которая ставит в соответствие сообщению 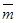 число
число 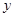 .
.
Практически невозможно изменить основной текст 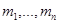 , не изменив
, не изменив 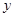 . Поэтому
. Поэтому 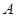 достаточно снабдить только число
достаточно снабдить только число 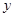 подписью, и эта подпись будет относиться ко всему сообщению
подписью, и эта подпись будет относиться ко всему сообщению 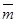 .
.
Далее 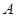 вычисляет число
вычисляет число 
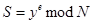 , т.е. она возводит число
, т.е. она возводит число 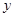 в свою секретную степень. Число
в свою секретную степень. Число 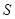 – цифровая подпись.
– цифровая подпись.
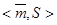 – вид сообщения с подписью.
– вид сообщения с подписью.
Теперь каждый, кто знает открытые параметры 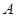 , т.е.
, т.е. 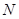 и
и 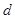 , может проверить подлинность его подписи.
, может проверить подлинность его подписи.
Для этого необходимо вычислить значение хеш-функции 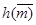 , т.е. число
, т.е. число 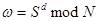 , и проверить равенство
, и проверить равенство 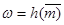 .
.
/*Пример*/ Электронная подпись RSA.
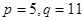
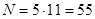
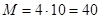
Пусть 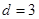
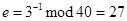 (алгоритм Евклида).
(алгоритм Евклида).
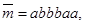
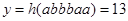 (допущение)
(допущение)
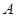 вычисляет
вычисляет 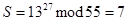
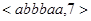 – сообщение с подписью
– сообщение с подписью
Вычисляем значение хеш-функции, получим 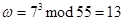
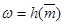
Подпись верна.
Определение Хеш-функции.
Хеш-функцией называется любая функция 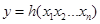 , которая строке сообщения
, которая строке сообщения 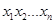 произвольной длины
произвольной длины 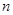 ставит в соответствие целое число фиксированной длины.
ставит в соответствие целое число фиксированной длины.
Криптографические алгоритмы
Шифр Эль-Гамаля
Пусть имеются абоненты 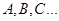 , которые хотят передавать друг другу зашифрованные сообщения, не имея никаких защищённых каналов связи.
, которые хотят передавать друг другу зашифрованные сообщения, не имея никаких защищённых каналов связи.
Для всей группы абонентов выбирается некоторое большое простое число 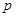 и число
и число 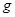 , такие, что различные степени
, такие, что различные степени 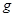 – различные числа по модулю
– различные числа по модулю 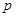 . Числа
. Числа 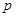 и
и 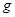 передаются абонентам в открытом виде.
передаются абонентам в открытом виде.
Затем каждый абонент выбирает своё секретное число 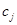 ,
, 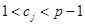 , и вычисляет соответствующе ему открытое число
, и вычисляет соответствующе ему открытое число 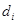 ,
,
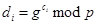 (
( 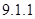 )
)
В результате получаем следующую таблицу ().
| Абонент | Открытый ключ | Секретный ключ |
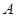
| 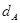
| 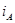
|
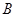
| 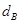
| 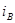
|
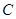
| 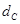
| 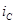
|
Табл(). Ключи пользователей в системе Эль=Гамаля.
Алгоритм передачи сообщения 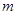 от
от 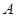 к
к 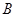 выглядит следующим образом: будем считать, что сообщение
выглядит следующим образом: будем считать, что сообщение 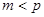 .
.
Шаг 1. Алиса формирует случайное число 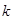 ,
, 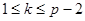 , вычисляет числа:
, вычисляет числа:
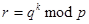 (9.1.2)
(9.1.2)
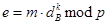 (9.1.3)
(9.1.3)
и передаёт пару чисел 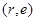 абоненту Бобу.
абоненту Бобу.
Шаг 2. Боб, получив 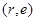 , вычисляет
, вычисляет
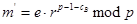 (9.1.4)
(9.1.4)
/*Пример*/
Алиса хочет передать Бобу сообщение 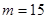 . Допустим
. Допустим 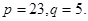 Пусть Боб выбрал для себя секретное число
Пусть Боб выбрал для себя секретное число 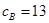 и вычислил по формуле (9.1.1)
и вычислил по формуле (9.1.1)
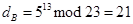
Алиса выбирает случайное число 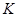 , например
, например 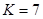 , и вычисляет по (9.1.2) и (9.1.3):
, и вычисляет по (9.1.2) и (9.1.3):
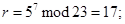
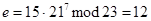 .
.
Теперь Алиса посылает Бобу шифрограмму (17,12). Боб вычисляет по формуле (9.1.4):
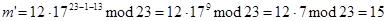
Боб расшифровал сообщение
Электронная подпись на базе Эль-Гамаля.
Алиса выбирает большое простое число 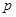 и число
и число 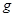 , такие, что различные степени
, такие, что различные степени 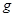 – это различные числа по модулю
– это различные числа по модулю 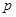 . Эти числа передаются или хранятся в открытом виде и могут быть общими для целой группы пользователей. Алиса выбирает случайное число
. Эти числа передаются или хранятся в открытом виде и могут быть общими для целой группы пользователей. Алиса выбирает случайное число 
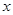 ,
, 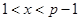 , которое она держит в секрете. Это её секретный ключ.
, которое она держит в секрете. Это её секретный ключ.
Затем она вычисляет число
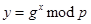 (9.1.5)
(9.1.5)
Это число 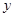 Алиса публикует в качестве открытого ключа. Заметим, что при больших
Алиса публикует в качестве открытого ключа. Заметим, что при больших 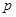 , зная
, зная 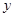 , невозможно найти
, невозможно найти 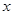 (это задача дискретного логарифмирования).
(это задача дискретного логарифмирования).
Теперь Алиса может подписывать сообщения. Допустим, она хочет подписать сообщение 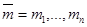 . Опишем последовательность действий для построения подписи.
. Опишем последовательность действий для построения подписи.
Вначале Алиса вычисляет значение хеш-функции для сообщения 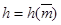 , которое должно удовлетворять неравенству
, которое должно удовлетворять неравенству 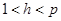 . Затем Алиса случайным образом выбирает число
. Затем Алиса случайным образом выбирает число 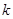
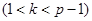 , взаимно простое число с
, взаимно простое число с 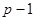 , и вычисляет число:
, и вычисляет число:
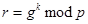 (9.1.6)
(9.1.6)
Далее Алиса вычисляет числа:
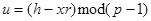 (9.1.7)
(9.1.7)
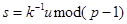 (9.1.8).
(9.1.8).
Под 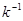 в (9.1.8) подразумевается число, удовлетворяющее уравнению
в (9.1.8) подразумевается число, удовлетворяющее уравнению
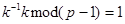 (9.1.9)
(9.1.9)
Такое 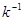 существует, так как
существует, так как 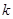 и
и 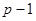 взаимно просты, и может быть найдено по алгоритму Евклида. Наконец Алиса формирует подписанное сообщение
взаимно просты, и может быть найдено по алгоритму Евклида. Наконец Алиса формирует подписанное сообщение
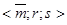 (9.1.10).
(9.1.10).
Получив сообщение Боб заново вычисляет значение хеш-функции 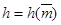 и проверяет подпись, используя равенство
и проверяет подпись, используя равенство
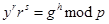
 (9.1.11)
(9.1.11)
/*Пример*/
Пусть общие параметры для некоторого сообщества пользователей 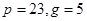 . Алиса выбирает свой секретный ключ
. Алиса выбирает свой секретный ключ 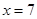 и вычисляет открытый ключ
и вычисляет открытый ключ 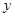 по формуле (9.1.5):
по формуле (9.1.5):
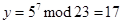
Пусть Алиса создала документ 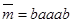 и хочет его подписать. Прежде всего Алиса вычисляет хеш-функцию, пусть её значение будет равно
и хочет его подписать. Прежде всего Алиса вычисляет хеш-функцию, пусть её значение будет равно 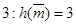 . Затем Алиса генерирует случайное число
. Затем Алиса генерирует случайное число 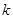 , например,
, например, 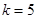 .
.
|
из
5.00
|
Обсуждение в статье: Электронная подпись (цифровая подпись). |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

