 |
Главная |
ЭНТРОПИЯ ИСТОЧНИКА СООБЩЕНИЙ
|
из
5.00
|
Получатель знает весь набор возможных сообщений, которые могут быть ему направлены, но какое именно сообщение передано ему сейчас – для него тайна. Именно в этом и заключается неопределенность состояния получателя. Если сообщение принято и есть уверенность, что понято правильно, то неопределенность исчезает. Другими словами сообщение содержало в себе ровно столько информации, сколько было неопределенности у получателя.
Таким образом, центральным вопросом становится способ определения меры неопределенности сообщения. Эта величина называется энтропией (точно также как в статистической термодинамике).
Если источник информации  , располагающий алфавитом из
, располагающий алфавитом из 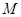 букв, передал «случайно для себя» букву
букв, передал «случайно для себя» букву 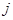 , то количество переданной информации составит, согласно Шеннону, величину
, то количество переданной информации составит, согласно Шеннону, величину  . Чем больше вероятность
. Чем больше вероятность  , тем меньшее количество информации было передано. Для лучшего понимания этого приведем пример. Хороший (успевающий) студент пошел сдавать экзамен. Априори известно, что с вероятностью
, тем меньшее количество информации было передано. Для лучшего понимания этого приведем пример. Хороший (успевающий) студент пошел сдавать экзамен. Априори известно, что с вероятностью  он сдаст экзамен (по крайней мере, статистика предшествующих сессий давала основания так полагать), а с вероятностью
он сдаст экзамен (по крайней мере, статистика предшествующих сессий давала основания так полагать), а с вероятностью  – «провалится». Какое количество информации мы получим, узнав о результате экзамена? Если экзамен сдан, то
– «провалится». Какое количество информации мы получим, узнав о результате экзамена? Если экзамен сдан, то  бит. Мы получили маленькое количество информации, да это и понятно, мы и без того знали, что студент хороший. Но если он «провалил» экзамен, то это неожиданная новость. Она несет в себе много информации -
бит. Мы получили маленькое количество информации, да это и понятно, мы и без того знали, что студент хороший. Но если он «провалил» экзамен, то это неожиданная новость. Она несет в себе много информации - 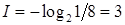 бита.
бита.
Таким образом, количество передаваемой информации зависит от того, какое именно сообщение передано, а это сообщение случайно! Поэтому
 (1)
(1)
носит название случайной энтропии. Обычно в теории информации работают со средними значениями, поэтому источник принято характеризовать средней (больцмановской) энтропией, определяемой по формуле:
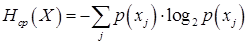 . (2)
. (2)
Здесь под символом  понимается
понимается  – все множество реализаций источника, т.е. его алфавит. Далее значок среднего будем опускать, понимая под энтропией именно среднюю энтропию, энтропию конкретного сообщения будем оговаривать отдельно.
– все множество реализаций источника, т.е. его алфавит. Далее значок среднего будем опускать, понимая под энтропией именно среднюю энтропию, энтропию конкретного сообщения будем оговаривать отдельно.
Можно показать, что средняя энтропия максимальна, если все сообщения равновероятны, т.е.
 и
и  . (3)
. (3)
Алфавит может иметь вероятностное распределение, далекое от равномерного. Если некоторый исходный алфавит содержит  символов, то его имеет смысл сравнить с «оптимизированным алфавитом», вероятностное распределение которого равномерно. Разность между максимально возможным значением энтропии сообщения –
символов, то его имеет смысл сравнить с «оптимизированным алфавитом», вероятностное распределение которого равномерно. Разность между максимально возможным значением энтропии сообщения –  и средней энтропией рассматриваемого источника –
и средней энтропией рассматриваемого источника –  принято называть избыточностью источника сообщений
принято называть избыточностью источника сообщений  :
:
 . (4)
. (4)
Избыточность показывает, насколько в среднем неплотно, при заданном алфавите, «упакована» информация в сообщениях источника. В частности избыточность современного английского текста составляет 50%, избыточность русского текста - 70%.
КОДЕР ИСТОЧНИКА
Для уменьшения избыточности источника  используют энтропийное кодирование – кодирование словами (кодами) переменной длины, при которой длина кода символа имеет обратную зависимость от вероятности появления символа в передаваемом сообщении. Обычно энтропийные кодировщики используют для сжатия данных коды, длины которых пропорциональны отрицательному логарифму вероятности символа. Таким образом, наиболее вероятные символы используют наиболее короткие коды.
используют энтропийное кодирование – кодирование словами (кодами) переменной длины, при которой длина кода символа имеет обратную зависимость от вероятности появления символа в передаваемом сообщении. Обычно энтропийные кодировщики используют для сжатия данных коды, длины которых пропорциональны отрицательному логарифму вероятности символа. Таким образом, наиболее вероятные символы используют наиболее короткие коды.
КОД ШЕННОНА–ФАНО
Код Шеннона – Фано представляет собой метод сжатия информации схожий с алгоритмом Хаффмана, который появился несколькими годами позже. Алгоритм использует коды переменной длины: часто встречающийся символ кодируется кодом меньшей длины, редко встречающийся — кодом большей длины. Коды Шеннона — Фано префиксные, то есть никакое кодовое слово не является префиксом (группой первых символов) любого другого слова. Это свойство позволяет однозначно декодировать любую последовательность кодовых слов.
Основные этапы создания кода.
1. Символы первичного алфавита М1 выписывают в порядке убывания вероятностей.
2. Символы полученного алфавита делят на две части, суммарные вероятности символов которых максимально близки друг другу.
3. В префиксном коде для первой части алфавита присваивается двоичная цифра «0», второй части — «1».
4. Полученные части рекурсивно делятся и их частям назначаются соответствующие двоичные цифры в префиксном коде.
Код Шеннона — Фано строится с помощью дерева. Построение этого дерева начинается от корня. Всё множество кодируемых элементов соответствует корню дерева (вершине первого уровня). Оно разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Эти подмножества соответствуют двум вершинам второго уровня, которые соединяются с корнем. Далее каждое из этих подмножеств разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Им соответствуют вершины третьего уровня. Если подмножество содержит единственный элемент, то ему соответствует концевая вершина кодового дерева; такое подмножество разбиению не подлежит. Подобным образом поступаем до тех пор, пока не получим все концевые вершины. Ветви кодового дерева размечаем символами 1 и 0, как в случае кода Хаффмана.
При построении кода Шеннона — Фано разбиение множества элементов может быть произведено, вообще говоря, несколькими способами. Выбор разбиения на уровне n может ухудшить варианты разбиения на следующем уровне (n + 1) и привести к неоптимальности кода в целом. Другими словами, оптимальное поведение на каждом шаге пути ещё не гарантирует оптимальности всей совокупности действий. Поэтому код Шеннона — Фано не является оптимальным в общем смысле, хотя и дает оптимальные результаты при некоторых распределениях вероятностей. Для одного и того же распределения вероятностей можно построить, вообще говоря, несколько кодов Шеннона — Фано, и все они могут дать различные результаты. Если построить все возможные коды Шеннона — Фано для данного распределения вероятностей, то среди них будут находиться и все коды Хаффмана, то есть оптимальные коды.
Кодирование Шеннона — Фано является достаточно старым методом сжатия, и на сегодняшний день оно не представляет особого практического интереса. В большинстве случаев длина последовательности, сжатой по данному методу, равна длине сжатой последовательности с использованием кодирования Хаффмана. Но на некоторых последовательностях могут сформироваться неоптимальные коды Шеннона — Фано, поэтому более эффективным считается сжатие методом Хаффмана.
Пример построения кодового дерева Шеннона - Фано
Исходные символы:
A (частота встречаемости 50),
B (частота встречаемости 39),
C (частота встречаемости 18),
D (частота встречаемости 49),
E (частота встречаемости 35),
F (частота встречаемости 24).

Рис.2. Кодовое дерево
Полученный код: A — 11, B — 101, C — 100, D — 00, E — 011, F — 010.
КОД ХАФФМАНА
Этот метод кодирования состоит из двух основных этапов:
– построение оптимального кодового дерева;
– построение отображения «код – символ» на основе построенного дерева.
Алгоритм построения кода Хаффмана.
1. Подсчитываются вероятности  появления символов
появления символов  первичного алфавита в исходном тексте (если они не заданы заранее).
первичного алфавита в исходном тексте (если они не заданы заранее).
2. Символы первичного алфавита выписывают в порядке убывания вероятностей.
3. Последние два символа в упорядоченном списке объединяют в один и вставляют его в соответствующей позиции, предварительно удалив символы, вошедшие в объединение. Вероятность возникшего нового символа равна суммарной вероятности удаленных. Затем вставляют новый символ в список остальных на соответствующее место (повторяют ранжирование списка по вероятности).
4. Предыдущий шаг повторяют до тех пор, пока в списке остается более одного символа.
Этот процесс можно представить как построение дерева, корень которого — символ с вероятностью 1, получившийся при объединении символов последнего шага, два его предшественника - символы из предыдущего шага.
Каждые два элемента, стоящие на одном уровне, нумеруются: 0 или 1. Коды получаются из путей - от первого потомка корня и до листка. При декодировании можно использовать то же самое дерево: считывается по одной цифре и делается шаг по дереву, пока не достигается лист. Затем выводится символ, стоящий в листе, и производится возврат в корень.
Построение дерева Хаффмана
Бинарное дерево, соответствующее коду Хаффмана, называют деревом Хаффмана. Задача построения кода Хаффмана равносильна задаче построения соответствующего ему дерева.
Общая схема построения дерева Хаффмана выглядит следующим образом.
1. Составляется список кодируемых символов.
2. Из списка выбирается 2 узла с наименьшим весом (под весом следует понимать частоту использования символа или вероятность его появления – чем чаще используется, тем больше весит ).
3. Сформируем новый узел и присоединим к нему, в качестве дочерних, два узла выбранных из списка. При этом вес сформированного узла положим равным сумме весов дочерних узлов.
4. Удалим выбранные узлы из списка.
5. Добавим вновь сформированный узел к списку.
6. Если в списке больше одного узла, то повторить п.п. 2-6.
Пример построения кода и дерева Хаффмана
Рассмотрим на примере источника с алфавитом мощностью 9 , задаваемого множеством пар  , метод кодирования по Хаффману. Конкретные значения этого множества представлены в табл. 4.
, метод кодирования по Хаффману. Конкретные значения этого множества представлены в табл. 4.
Таблица 4
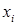
| 
| 
| 
| 
| 
| 
| 
| 
| 
|

| 0.20 | 0.15 | 0.15 | 0.12 | 0.10 | 0.10 | 0.08 | 0.06 | 0.04 |
Таблица 5
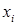
| 
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | Код. |

| 0.20 |
| 11 | |||||||

| 0.15 | 001 | ||||||||

| 0.15 | 011 | ||||||||

| 0.12 | 010 | ||||||||

| 0.10 | 101 | ||||||||

| 0.10 | 100 | ||||||||

| 0.08 | 0001 | ||||||||
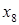
| 0.06 | 00001 | ||||||||

| 0.04 | 00000 | ||||||||
В рисунке табл. 5 приведены все объединения, указанные в алгоритме Хаффмана. Нетрудно убедиться, что «дерево», изображенное на рис. 3, получено простым поворотом на  рисунка табл. 5. Рассмотрим движение по ветвям дерева от корня к листьям. Договоримся, что при каждом повороте направо будем записывать «0», а при повороте налево - «1».
рисунка табл. 5. Рассмотрим движение по ветвям дерева от корня к листьям. Договоримся, что при каждом повороте направо будем записывать «0», а при повороте налево - «1».
|

Рис. 3. Схема реализации алгоритма Хафманна
При движении от корня к листу  мы дважды «повернем» направо, поэтому такому символу припишем кодовое слово -11. При движении к листу
мы дважды «повернем» направо, поэтому такому символу припишем кодовое слово -11. При движении к листу 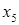 мы один раз повернем направо, затем налево и потом снова направо. Это дает кодовое слово – 101. Процедуру определения кодовых слов без труда можно продолжить.
мы один раз повернем направо, затем налево и потом снова направо. Это дает кодовое слово – 101. Процедуру определения кодовых слов без труда можно продолжить.
Дерево Хаффмана в стандартном виде представлено на рис. 4. На нем каждому повороту направо или налево предыдущей схемы поставлены в соответствие стрелочки  и
и  .
.


Рис. 4. Дерево Хаффмана для рассматриваемого примера
|
из
5.00
|
Обсуждение в статье: ЭНТРОПИЯ ИСТОЧНИКА СООБЩЕНИЙ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы


