Вариация, дисперсия баллов и дифференцирующая способность.

Если на какое-то задание правильно отвечают все тестируемые, то такое задание становится не тестовым. Испытуемые отвечали на него одинаково; между ними нет вариации. Соответственно, по данному заданию в матрице будут стоять одни единички.

Не тестовым надо считать и то задание, на которое нет ни одного правильного ответа; в матрице по нему ставят, соответственно, одни нули. Вариация по нему также равна нулю. Нулевая вариация означает практическую необходимость удаления задания из проектируемого теста. Оно, для данной группы, не тестовое. Возможно, в другой группе это задание заработает, но это будет задание уже другого, а не данного теста, если под тестом понимать метод и результат измерения знаний.

Удобной мерой вариации является значение дисперсии баллов, обозначаемой символом 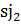 . Для заданий, в которых используется только дихотомическая оценка (1 или 0), мера вариации определяется по сравнительно простой формуле:

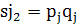 (5)

Значения дисперсии по каждому заданию, рассчитанные по этой формуле, представлены в пятой строке нижней части таблицы 2.

Помимо вариации баллов в каждом задании считается вариация тестовых баллов испытуемых, набранных ими в тесте, по всем заданиям. Расчет показателей вариации тестовых баллов начинается с определения суммы квадратов отклонений значений баллов от среднего арифметического тестового балла ( 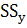), по формуле:

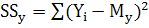 (6)

Для данных таблицы 2:

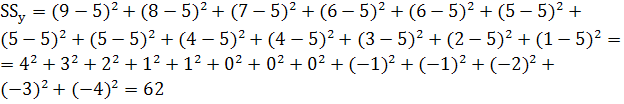 (7)

У показателя SSy тоже есть недостаток, который заключается в его зависимости от числа испытуемых: при прочих равных условиях, чем больше группа, тем большей оказывается 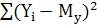, что делает этот показатель несопоставимым для групп с разным числом испытуемых. Поэтому для исправления отмеченного недостатка используют второй прием - делят  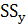на число испытуемых в группе. В результате получается стандартный показатель вариации тестовых баллов, называемый дисперсией  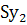или, по-старому, вариансой.

Для тестовых баллов в столбце 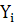 табл. на рис.2 дисперсия вычисляется по формуле:

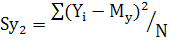 (8)

При N, равном тринадцати испытуемым, дисперсия равна:

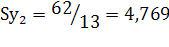 (9)

Для удобства в интерпретации тестовых результатов вместо дисперсии часто используется стандартное отклонение тестовых баллов от средней арифметической. Оно обозначается символом Sy и вычисляется как корень квадратный из значения sy2.

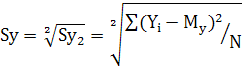 (10)

Стандартное отклонение Sy является общепринятой мерой вариации тестовых баллов.

Подставляя наши данные, получаем

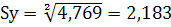 (11)

Дифференцирующая способность является четвертым требованием к тестовым заданиям.

Если на какое-то задание правильно отвечают все тестируемые, то такое задание не дифференцирует сильных от слабых и потому ему в тесте делать нечего. Нет в тесте места и тем заданиям, на которые нет ни одного правильного ответа; в матрице по ним ставят одни нули.