 |
Главная |
ДИСЦИПЛИНА «МАТЕМАТИКА»
|
из
5.00
|
Вопросы для оценки качества освоения курса
1. Понятие матрицы. Виды матриц.
2. Операции над матрицами (умножение матрицы на число; сложение, вычитание, умножение матриц, возведение в степень, транспонирование матриц).
3. Определители квадратных матриц.
4. Минор элемента матрицы, алгебраическое дополнение элемента матрицы.
5. Свойства определителей.
6. Понятие обратной матрицы, необходимое и достаточное условие существования обратной матрицы, алгоритм вычисления обратной матрицы.
7. Понятие ранга матрицы.
8. Понятие системы линейных уравнений (совместная, несовместная, определенная, неопределенная система).
9. Решение системы линейных уравнений методом обратной матрицы и с помощью формул Крамера.
10. Уравнение линии на плоскости.
11. Уравнение прямой с угловым коэффициентом.
12. Уравнение прямой, проходящей через данную точку в данном направлении.
13. Уравнение прямой, проходящей через две данные точки (каноническое уравнение прямой).
14. Уравнение прямой в отрезках.
15. Общее уравнение прямой.
16. Условия параллельности и перпендикулярности прямых.
17. Расстояние от точки до прямой.
18. Уравнение прямой, проходящей через точку параллельно направляющему вектору.
19. Абсолютная величина действительного числа, окрестность точки.
20. Понятие функции, зависимая переменная, независимая переменная (аргумент), область определения функции, область значений функции, способы задания функции.
21. Основные свойства функций.
22. Явная, неявная функции; обратная, сложная функции.
23. Преобразование графиков.
24. Понятие числовой последовательности, предел числовой последовательности, геометрический смысл предела числовой последовательности.
25. Предел функции в бесконечности и в точке.
26. Бесконечно малые величины, их связь с пределами функций, их свойства.
27. Бесконечно большие величины, их свойства, связь между бесконечно малыми и бесконечно большими величинами.
28. Основные теоремы о пределах, признаки существования предела.
29. Замечательные пределы.
30. Непрерывность функции, свойства непрерывных функций в точке, свойства непрерывных функций на отрезке.
31. Определение производной, зависимость между непрерывностью и дифференцируемостью функции.
32. Правила дифференцирования.
33. Производная сложной и обратной функции.
34. Производные высших порядков.
35. Основные теоремы дифференциального исчисления.
36. Правило Лопиталя.
37. Возрастание и убывание функций.
38. Экстремум функции.
39. Наибольшее и наименьшее значения функции на отрезке.
40. Выпуклость функции точки перегиба.
41. Асимптоты графика функции.
42. Понятие дифференциала функции, дифференциалов высших порядков.
43. Первообразная функция и неопределенный интеграл.
44. Свойства неопределенного интеграла.
45. Методы замены переменной.
46. Метод интегрирования по частям.
47. Интегрирование простейших рациональных дробей.
48. Интегрирование некоторых видов иррациональностей.
49. Интегрирование тригонометрических функций.
50. Понятие определенного интеграла, его геометрический смысл.
51. Свойства определенного интеграла.
52. Формула Ньютона-Лейбница.
53. Понятие несобственного интеграла.
54. Приближенное вычисление определенного интеграла (формула трапеций).
55. Понятие функции нескольких переменных.
56. Окрестность точки (двумерный случай), график функции двух переменных.
57. Передел функции двух переменных.
58. Понятие непрерывности функции двух переменных.
59. Частная производная функции нескольких переменных.
60. Дифференциал функции двух переменных.
61. Понятие дифференцируемой функции двух переменных в точке.
62. Достаточное условие дифференцируемости.
63. Понятие производной по направлению.
64. Градиент функции.
65. Экстремум функции двух переменных, необходимое условие экстремума.
66. Критические (стационарные) точки функции двух переменных, достаточное условие экстремума.
67. Исследование функции двух переменных на экстремум.
68. Метод наименьших квадратов.
Литература
Высшая математика для экономистов: Учебн. пособие для вузов / Н.Ш.Кремер, Б.А.Путко, И.М.Тишин, М.Н.Фридман; Под ред. Н.Ш.Кремера. – М.: Банки и биржи, ЮНИТИ, 1997. – 439 с.
Контрольная работа № 2
Вариант 1
1. Длительность лечения в стационаре 45 больных (в днях):
11, 14, 14, 17, 17, 19, 19, 19, 18, 18, 18, 18, 19, 19, 18, 18, 17, 17, 19, 24, 12, 13, 24, 23, 23, 24, 21, 22, 21, 23, 22, 21, 22, 20, 20, 20, 15, 15, 16, 20, 20, 16, 16, 20, 26.
Построить гистограмму частот распределения длительности лечения, сгруппировав данные в 5 интервалов.
2. Частота пульса у 10 лиц:
83, 91, 102, 95, 90, 100, 88, 81, 86, 84.
Сделайте интервальную оценку частоты пульса с надежностью 0,95.
3. Число состоящих на диспансерном учете больных у 9 участковых врачей: 114, 123, 136, 148, 130, 151, 141, 143, 120.
По приведенным данным оценить генеральную среднюю и генеральную дисперсию числа диспансерных больных.
4. Оценить характер связи между числом послеоперационных осложнений (Y) и временем (Х), прошедшим от момента приступа холецистита до начала операции
| X (час) | 2 | 4 | 6 | 11 | 12 | 16 | 19 | 22 | 24 |
| Y | 6 | 8 | 12 | 19 | 20 | 24 | 28 | 34 | 46 |
Записать уравнение регрессии Y по Х.
Вариант 2
1. Частота дыхания у 47 мужчин в возрасте 40-45 лет:
12, 12, 17, 12, 14, 13, 13, 14, 14, 15, 15, 16, 16, 16, 19, 19, 20, 20, 20, 20, 21,19, 13, 15, 12, 15, 17, 16, 17, 13, 16, 17, 18, 16, 18, 14, 15, 14, 17, 18, 14, 18, 20, 17, 18, 19, 22.
Построить гистограмму относительных частот распределения частоты дыхания, сгруппировав данные в 5 интервалов.
2. Частота дыхания у 8 мужчин в возрасте 35 лет:
19, 22, 21, 15, 16, 20, 25, 19.
Найти доверительный интервал для среднего значения частоты дыхания с доверительной вероятностью 0,95.
3. Уровни систолического (Х) и диастолического (Y) давления (в мм рт.ст.) у 12 здоровых юношей в возрасте 18 лет составили:
| X | 120 | 105 | 115 | 115 | 110 | 110 | 120 | 120 | 120 | 125 | 110 | 125 |
| Y | 80 | 65 | 70 | 65 | 65 | 70 | 75 | 75 | 70 | 75 | 70 | 80 |
Существует ли корреляционная связь между X и Y? Оценить ее количественно. Записать уравнение регрессии Y по Х.
4. При измерении размеров вируса орнитоза получены следующие величины (в мкм): 0,34; 0,45; 0,20; 0,29; 0,40. По приведенным данным оценить генеральную среднюю и генеральную дисперсию.
Вариант 3
1. Частота пульса у 55 студентов перед экзаменом составила:
64, 74, 78, 74, 74, 74, 60, 66, 62, 64, 68, 70, 66, 70, 68, 62, 68, 70, 72, 60, 76, 70, 74, 62, 70, 72, 72, 64, 70, 72, 66, 76, 68, 70, 58, 76, 74, 76, 76, 72, 76, 82, 74, 79, 78, 78, 76, 78, 76, 80, 80, 80, 78, 78, 81.
Построить гистограмму распределения частоты пульса, сгруппировав данные в 6 интервалов.
2. На 15 лекциях по математической статистике на одном из потоков присутствовало студентов:
104, 113, 120, 98, 105, 88, 102, 110, 101, 99, 104, 98, 105, 97, 108.
Найти среднюю выборочную и исправленную дисперсию числа студентов на лекции.
3. Оценить характер связи между ростом (Х) и массой (Y) тела студентов в возрасте 20 лет.
| X(см) | 155 | 180 | 158 | 160 | 170 | 165 | 167 | 162 | 171 | 174 | 168 | 176 |
| Y(кг) | 53 | 84 | 55 | 57 | 79 | 57 | 58 | 60 | 63 | 66 | 67 | 72 |
Записать уравнение регрессии Y по Х.
4. В результате измерения систолического артериального давления (в мм рт.ст.) у 11 детей в возрасте 7 лет получены следующие данные:
90, 105, 95, 110, 115, 120, 120, 120, 115, 100, 120.
Найти доверительный интервал для среднего значения систолического давления с надежностью 0,95.
Вариант 4
1. Длительность нетрудоспособности (в днях) у 35 больных с ОРЗ:
3, 5, 2, 3, 4, 5, 6, 6, 6, 9, 6, 5, 7, 6, 6, 7, 5, 9, 10, 8, 7, 14, 13, 5, 6, 7, 8, 7, 5, 6, 4, 9, 8, 7, 12.
Построить гистограмму относительных частот распределения длительности нетрудоспособности, сгруппировав данные в 4 интервала.
2. У 12 матерей, имеющих пороки сердца, родились дети с массой тела (в кг): 3,0; 2,5; 2,6; 3,0; 3,1; 2,9; 2,8; 2,6; 2,3; 2,9; 3,2; 2,7.
По приведенным данным оценить выборочную среднюю и выборочную дисперсию массы тела новорожденных.
3. Смертность (Y) от сосудистых поражений головного мозга на 10000 женщин в зависимости от возраста (Х) составила:
| Х год | 17 | 22 | 27 | 32 | 37 | 42 | 47 | 52 | 57 | 62 | 72 | 77 | 80 |
| Y % | 5 | 5,5 | 5,6 | 5,7 | 5,6 | 7,6 | 7,7 | 9,3 | 10,7 | 10,4 | 14,1 | 15,0 | 23,2 |
Оценить характер связи между Х и Y . Записать уравнение регрессии Y по Х.
4. Для оценки функционального состояния получены следующие значения пульса на лучевой артерии лиц среднего возраста:
60, 62, 63, 64, 65, 68, 72, 74.
Найти доверительный интервал для среднего значения пульса с надежностью 0,95.
Вариант 5
1. Число состоящих на диспансерном учете больных у 33 невропатологов поликлиник крупного города:
64, 60, 66, 62, 64, 68, 70, 66, 70, 68, 62, 68, 70, 72, 60, 76, 70, 74, 62, 70,
72, 72, 64, 70, 72, 66, 76, 68, 70, 58, 76, 74, 76, 82, 76, 72, 76, 74, 79, 78,
74, 78, 74, 74, 74, 78, 76, 78, 76, 80, 80, 80, 78, 78, 81.
Построить гистограмму относительных частот распределения числа больных, сгруппировав данные в 6 интервалов.
2. Сделать интервальную оценку роста 10 мальчиков в возрасте 2 лет (в см) по полученным данным: 90, 92, 95, 91, 93, 96, 94, 93, 89, 97. Надежность взять равной 0,95.
3. Измерение веса Х (кг) девочек в возрасте 10 лет дало следующие результаты:
| X | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
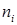 (частота) (частота)
| 2 | 1 | 6 | 8 | 21 | 20 | 18 | 12 | 3 | 4 | 2 | 3 |
Найти выборочную среднюю и дисперсию веса девочек.
4. Число осложненных родов (Y%) в зависимости от возраста рожениц (Х) дано в таблице:
| X | 16 | 18 | 22 | 25 | 30 | 35 | 40 |
| Y(%) | 5 | 3 | 4 | 5 | 8 | 12 | 20 |
Оценить характер связи между Х и Y. Записать уравнение регрессии Y по Х.
Вариант 6
1. Лихорадочный период при пневмонии у 32 больных (число дней):
3, 8, 14, 14, 7, 6, 4, 12, 13, 3, 4, 5, 10, 11, 15, 10, 10, 11, 12, 8, 9, 7, 7, 8, 9, 9, 7, 8, 12, 6, 10, 9.
Построить гистограмму относительных частот распределения лихорадочного периода, сгруппировав данные в 4 интервала.
2. Под наблюдением 7 участковых педиатров детской поликлиники состояло детей первого года жизни: 52, 60, 53, 64, 62, 54, 61.
Найти среднюю выборочную и исправленную дисперсию числа детей, находящихся под наблюдением.
3. В результате измерений диаметра 15 эритроцитов больного получены следующие данные (мкм): 5,1; 5,8; 4,6; 4,7; 4,5; 5,1; 5,9; 6,1; 6,7; 4,1; 3,8; 6,0; 5,9; 5,7; 6,8. Найти доверительный интервал для среднего значения диаметра эритроцита с надежностью 0,99.
4. Существует ли связь между дозой принимаемого препарата Х (мг) и скоростью выздоровления Y (дней). Оценить связь.
| X | 3,5 | 2 | 2 | 1,2 | 1,4 | 1,4 | 0,5 |
| Y | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
Записать уравнение регрессии Y по Х.
Вариант 7
1. Частота дыхания у 47 мужчин в возрасте 40-45 лет:
12, 15, 13, 14, 15, 16, 16, 19, 19, 20, 20, 20, 19, 14, 15, 12, 15, 13, 14, 12, 18, 12, 17, 16, 18, 13, 16, 17, 17, 14, 15, 17, 18, 14, 15, 14, 16, 18, 14, 18, 20, 16, 18, 19, 22, 21, 20.
Построить гистограмму относительных частот распределения частоты дыхания, сгруппировав данные в 5 интервалов.
2. Частота пульса у 10 лиц:
81, 90, 101, 95, 91, 100, 88, 80, 85, 85.
Сделайте интервальную оценку частоты пульса с надежностью 0,95.
3. Измерение веса Х (кг) девочек в возрасте 10 лет дало следующие результаты:
| X | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
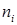 (частота) (частота)
| 1 | 3 | 5 | 9 | 20 | 20 | 19 | 11 | 4 | 3 | 2 | 3 |
Найти выборочную среднюю и дисперсию веса девочек.
4. Оценить характер связи между ростом (Х) и массой (Y) тела студентов в возрасте 20 лет.
| X(см) | 157 | 180 | 158 | 160 | 170 | 165 | 167 | 162 | 171 | 174 | 168 | 176 |
| Y(кг) | 55 | 82 | 58 | 57 | 79 | 58 | 59 | 60 | 64 | 65 | 67 | 72 |
Записать уравнение регрессии Y по Х.
Вариант 8
1. Число состоящих на диспансерном учете больных гипертонической болезнью у 50 участковых терапевтов города:
21, 22, 20, 24, 25, 25, 26, 26, 27, 25, 25, 27, 24, 22, 23, 24, 39, 23, 40, 22, 25, 30, 26, 24, 25, 24, 25, 26, 28, 24, 30, 25, 26, 27, 30, 31, 34, 31, 35, 32, 30, 30, 25, 35, 28, 38, 39.
Построить гистограмму частот распределения больных, сгруппировав данные в 5 интервалов.
2. Рост мужчин (Х) в возрасте 40 лет дан в следующей таблице:
| X | 162 | 168 | 176 | 180 | 191 |
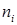 (частота) (частота)
| 10 | 25 | 12 | 10 | 3 |
Найти среднюю выборочную и дисперсию роста мужчин.
3. Вес новорожденных Х (кг) составляет:
| X | 2,4 | 2,6 | 3,0 | 3,2 | 3,5 | 4,0 |
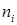 (частота) (частота)
| 1 | 8 | 12 | 10 | 5 | 1 |
Найти доверительный интервал для среднего значения веса новорожденных с надежностью 0,95.
4. Оценить характер связи между Х и Y:
| X | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 |
| Y | 0 | 0,3 | 1 | 1 | 2 | 2 | 2,75 | 3 | 3,5 | 4 | 4 |
Записать уравнение регрессии Y по Х.
Вариант 9
1. Длительность лечения в стационаре 45 больных пневмонией (в днях):
11, 12, 13, 24 , 24, 23, 23, 23, 22, 21, 24, 21, 22, 21, 14, 14, 22, 20, 20, 20, 15, 15, 20, 20, 20, 16, 16, 16, 17, 17, 19, 19, 19, 18, 18, 18, 18, 19, 19, 18, 18, 17, 17, 19, 26.
Построить гистограмму частот распределения длительности лечения, сгруппировав данные в 5 интервалов.
2. Частота пульса у 10 лиц:
80, 90, 100, 92, 90, 102, 88, 80, 85, 83.
Сделайте интервальную оценку средней частоты пульса с надежностью 0,95.
3. Число состоящих на диспансерном учете больных у 9 участковых врачей: 155, 132, 150, 140, 114, 122, 136, 145, 120.
По приведенным данным оценить генеральную среднюю и генеральную дисперсию числа диспансерных больных.
4. Оценить характер связи между числом послеоперационных осложнений (Y) и временем (Х), прошедшим от момента приступа холецистита до начала операции
| Х(час) | 2 | 4 | 7 | 10 | 13 | 16 | 19 | 22 | 24 |
| Y | 5 | 8 | 11 | 20 | 21 | 23 | 28 | 34 | 45 |
Записать уравнение регрессии Y по Х.
Вариант 10
1. Частота дыхания у 47 мужчин в возрасте 40-45 лет:
16, 16, 16, 20, 20, 20, 12, 12, 17, 12, 14, 13, 15, 19, 19, 19, 13, 15, 12, 15, 13, 14, 14, 15, 14, 14, 15, 16, 17, 16, 17, 13, 16, 17, 18, 18, 17, 18, 14, 18, 20, 20, 21, 22, 17, 18, 19.
Построить гистограмму относительных частот распределения частоты дыхания, сгруппировав данные в 5 интервалов.
2. Частота дыхания у 8 мужчин в возрасте 35 лет:
15, 16, 19, 20, 22, 21, 24, 19.
Найти доверительный интервал для среднего значения частоты дыхания с доверительной вероятностью 0,95.
3. Уровни систолического (Х) и диастолического (Y) давления (в мм рт.ст.) у 12 здоровых юношей в возрасте 18 лет составили:
| X | 120 | 105 | 115 | 115 | 110 | 110 | 120 | 120 | 120 | 125 | 110 | 125 |
| Y | 80 | 70 | 70 | 65 | 70 | 65 | 75 | 70 | 74 | 75 | 70 | 80 |
Существует ли корреляционная связь между X и Y? Оценить ее количественно. Записать уравнение регрессии Y по Х.
4. При измерении размеров вируса получены следующие величины (в мкм): 0,35; 0,44; 0,20; 0,30; 0,39. По приведенным данным оценить генеральную среднюю и генеральную дисперсию.
|
из
5.00
|
Обсуждение в статье: ДИСЦИПЛИНА «МАТЕМАТИКА» |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

