V . Диофантовы уравнения и алгебраические кривые (10 задач)

1. Найти все пифагоровы тройки (a, b, c), у которых c £ 30.
2. Доказать, что коника 3X ² + 6Y ² = 4 имеет рациональную точку. Найти все её рациональные точки.
3. На эллиптической кривой Y ² = X ³ – X найти точки порядка два, т.е. такие точки P, что 2P = O.
4. Найти многочлен, корнями которого являются координаты точек порядка три эллиптической кривой
   Y ² = X ³ + 1, т.е. таких точек P, что 3P = O.
5. Рассмотрим точку P = (3, 8) на кубической кривой  Y ² = X ³ – 43X + 166 над Q. Вычислить 2P, 3P, 4P и 8P. Сравнить 8P и P. Что из этого следует?

6. Найти многочлен, корнями которого являются абсциссы точек P  порядка 3 эллиптической кривой E над Q с уравнением Y ² = X ³ + 10X.

7. Вычислить группу C(F_p) для кривой y² = x³ + x + 1 и простых p = 3, 7, 11 и 13.

1. Найти точку пересечения параллельных прямых

L₁ : X + 2Y – Z = 0                   и                   L₂ : 2X + 4Y + Z = 0 

в P²(R).

1. Найти проективное замыкание окружности X ² + Y ² = 1 в P ²(C).

10. Найти все аффинные части проективной кривой X ² – YZ + 2XZ = 0.

11. *Кубическая кривая U ³ + V ³ = a (a ¹ 0) имеет рациональную точку (1 : -1 : 0) в бесконечности (т.е. это есть точка проективного замыкания данной кривой с однородным уравнением U ³ + V ³ = a W ³). Принимая эту рациональную точку за нейтральный элемент O, можно определить алгебраическую операцию над точками кривой, превращающую множество точек в группу. Вывести формулу для суммы P₁ + P₂ двух точек P₁ = (u₁, v₁) и P₂ = (u₂, v₂). Вывести формулу удвоения 2P точки P = (u, v).

12. *Проверить, что если u и v удовлетворяют соотношению U ³ + V ³ = a, то выражения

x =           и     y =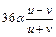

удовлетворяют соотношению Y ² = X ³ – 432a ². Предыдущие формулы задают преобразование кривой U ³ + V ³ = a в кривую Y ² = X ³ – 432a ². На каждой их этих кубических кривых определён групповой закон. Доказать, что указанное преобразование является изоморфизмом групп.

13. Вычислить значения квадратичного характера c(a) для всех a Î F_p, p = 5, 7, 11.

14. Пусть p – нечётное простое числа,  a, b, c Î Z,  p∤a. Доказать, что число решений сравнения  

aX ² + bX + c º 0 (mod p)

задаётся формулой N = 1 + c(D), где D = b² – 4ac.

15. Пусть p – нечётное простое число. Показать, что число решений сравнения X ² – Y ² º a (mod p) равно

N = p + .

16. *Пусть p ³ 3 есть простое число, а m ³ 1 есть целое, взаимно простое с p – 1. Доказать, что отображение x a x^m является изоморфизмом     на себя, уравнение x^m + y^m + z^m = 0 имеет в точности p + 1 проективное решение, где x, y, z Î F_p.

 

V I . Элементы теории дифференциальных уравнений (10 задач)

1.

V II . Комбинаторика (10 задач)

1. Нужно распределить преподавание в шести классах между тремя преподавателями. Сколькими способами можно произвести распределение, если каждый должен получить два класса?
2. *Доказать равенство

 

 

V I II . Заключение: множества, логика, аксиоматические теории (10 задач)

1. Пусть A, B и C – подмножества множества E. Доказать следующие равенства

· E \ (A \ B) = (E \ A) È (A Ç B),

· (E \ A) È (E \ (B È C)) = (E \ (A Ç B)) Ç (E \ (A Ç C)).

Примеры. 1) Пусть f(x) = x², g(y) = sin y. Тогда (g ◦ f)(x) = sin x², (f ◦ g)(y) = sin²y.

Примеры. 1) Отображение f : [0, ¥) ® R, x a x², как нетрудно видеть, инъективно. В то же время отображение f : R ® R, x a x² инъективным не является.

2) Отображение f : [-p / 2, p / 2] ® R, x a sin x является инъективным.

Примеры. 1) Отображение f : R ® [0, ¥), x a x² сюрьективно. В то же время отображение f : R ® R,
x a x² сюрьективным не является.

2) Отображение f : R ® [-1, 1], x a sin x является сюрьективным.

Примеры.

2) Отображение f : [0, ¥) ® [0, ¥), x a x² биективно.

3) Отображение f : [-p / 2, p / 2] ® [-1, 1] биективно.

4) Отображение f : {1,..., 5} ® {1,..., 5}, задаваемое таблицей

есть биекция множества {1,..., 5} на себя.

Примеры. 1) Для функции f : [0, ¥) ® [0, ¥), x a x² обратной является функция 

f ^-1 : [0, ¥) ® [0, ¥), x a .

2) Для функции f : [-p / 2, p / 2] ® [-1, 1], x a sin x существует обратная функция

f ^-1 : [-1, 1] ® [-p / 2, p / 2],

называемая арксинусом и обозначаемая y = arcsin x.

3) Функция f ^-1, обратная к биекции f из примера 4) к определению 1.3.7, задаётся таблицей

.

 

IX. Разное

 

1. Найти образ точки x = (1, 2) Î A²(R) при помощи проективного преобразования с матрицей M = .

[1] Знаком * отмечены чуть более трудные и длинные задачи.