Критерий относительных значений вероятностей состояний природы с учетом выигрышей (рисков)

 В практике принятия решений часто встречается случай, когда нам неизвестны вероятности состояний природы, но мы имеем представление о том, какие состояния природы более правдоподобны, какие менее правдоподобны, а какие равноправдоподобны. Поэтому мы можем расположить (неизвестные) вероятности состояний природы в виде убывающей или возрастающей последовательности. Для простоты предположим, что расположение q₁, ..., q_n уже и есть монотонная последовательность. Если, например, эта последовательность строго убывает, то правдоподобнее всех состояние П₁ затем по степени правдоподобности следует состояние П₂, и т. д., наименьшей правдоподобностью обладает состояние П _n. Не зная, на сколько одна вероятность состояния природы отличается от другой, мы можем предположительно придать им относительные значения, пропорциональные членам некоторой (подходящей на наш взгляд) монотонной последовательности положительных чисел τ₁, ..., τ_n, т.е.

                           q₁ : q₂ : q₃ : ... : q_n = τ₁ : τ₂ : τ₃ : ... : τ_n .                                      (18)

Из (18) следует, что если q₁ , ..., q_n убывающая, соответственно возрастаю­щая, последовательность, то убывающей, соответственно возрастающей, является и последовательность τ₁ , ..., τ_n.

При этом следует учитывать нормировочное равенство

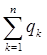                                        =1                                 (19)

Вероятность j-ого столбца определяется по формуле:

                                       q_j = 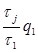, j=1, …, n                                   (20)

Из (20) и (19) получим:

                             1 = 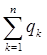 =  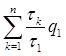= 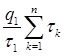.                 (21)

Из (21) выразим q₁ вероятность возникновения состояния природы П₁:

                                          q₁ = 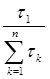.                                   (21)

Тогда:

                                           q_j = 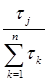.                                   (22)

Мы нашли значения вероятностей q_j, j=1, …, n, состояний природы.

Критерий Байеса относительно выигрышей при вероятностях состояний природы назовем критерием относительных значений вероятностей состояний природы с учетом выигрышей. При этом критерии показателем эффективности стратегии А _i является величина ā _i, получающаяся из равенства (6) подстановкой в него вероятностей (22):

                                 ā _i = 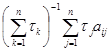, i=1, …, m.                         (23)

Так как множитель 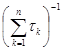  не зависит от номера i,то в качестве показателя эффективности стратегии А _i вместо величины (23) можно рассматривать величину:

                                  ā _i = 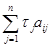, i=1, …, m.                                   (23)

Оптимальной среди чистых стратегий по рассматриваемому критерию является стратегия с максимальным показателем эффективности (23).

Критерий Байеса относительно рисков при вероятностях состояний природы назовем критерием относительных значений вероятностей состояний природы с учетом рисков. При этом показатель неэффективности стратегии подсчитывается по формуле (6), вероятности q₁ , ..., q_n в которой представлены формулой (2.20.31):

                                  ṝ_i = 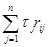, i=1, …, m.                                     (24)

Оптимальной среди чистых стратегий по обсуждаемому критерию является стратегия с минимальным показателем неэффективности (24).