 |
Главная |
Краевая задача и ее оператор
|
из
5.00
|
Уравнения в частных производных математической физики распадаются на два большие класса. Уравнения первого класса описывают процессы, в которых искомые величины заметно меняются с течением времени, то есть являются функциями пространственных координат и времени. Наиболее простой и важный представитель этого класса – волновое уравнение, частным случаем которого является уравнение колебания струны. Другой важный пример – уравнение теплопроводности.
Уравнения второго класса описывают явления стационарные. Чаще всего эти уравнения принадлежат к эллиптическому типу. Одна из простейших стационарных задач – задача о распределении температуры в ограниченном теле 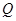 с границей
с границей 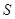 в случае отсутствия в теле источников тепла. Температура тела
в случае отсутствия в теле источников тепла. Температура тела 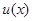 удовлетворяет уравнению Лапласа с тремя независимыми переменными
удовлетворяет уравнению Лапласа с тремя независимыми переменными
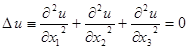 (1)
(1)
Принимаем, что на границе 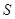 тела
тела 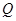 температура - известная функция координат (краевые условия 1 рода):
температура - известная функция координат (краевые условия 1 рода):
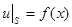 (2)
(2)
Задачу о распределении температур можно сформулировать так:
Найти функцию 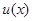 , которая удовлетворяет уравнению Лапласа (1) внутри области
, которая удовлетворяет уравнению Лапласа (1) внутри области 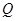 и принимает заданные значения (2) на ее границе
и принимает заданные значения (2) на ее границе 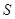 (Задача Дирихле для уравнения Лапласа).
(Задача Дирихле для уравнения Лапласа).
Условия на границе могут быть и другого типа. Если поток тепла через границу пропорционален разности температур внешней среды 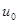 и границы тела
и границы тела 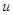 (
( 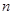 – внешняя нормаль к поверхности тела
– внешняя нормаль к поверхности тела 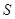 ), то получаем условия 3-ого рода:
), то получаем условия 3-ого рода:
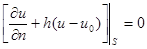 или
или 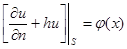 (3)
(3)
Если в условии (3) положить 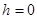 , то получаем краевое условие 2-ого рода
, то получаем краевое условие 2-ого рода
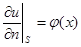 (4)
(4)
Задача интегрирования уравнения (1) с условием (4) называется задачей Неймана.
С краевой задачей математической физики можно связать некоторый оператор – «оператор данной краевой задачи», действующий в подходящем гильбертовом пространстве. При этом данная задача может быть записана в виде уравнения
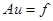 (5)
(5)
где 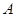 – оператор краевой задачи,
– оператор краевой задачи, 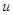 и
и 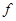 – элементы гильбертова пространства. Пример такой операторной задачи – однородная задача Дирихле для уравнения Пуассона (неоднородного уравнения Лапласа):
– элементы гильбертова пространства. Пример такой операторной задачи – однородная задача Дирихле для уравнения Пуассона (неоднородного уравнения Лапласа):
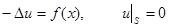 (6)
(6)
Решение задачи (6) ищем во множестве (линеале) 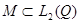 функций, обладающих следующими свойствами:
функций, обладающих следующими свойствами: 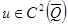 ,
, 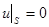 . На множестве М оператор
. На множестве М оператор 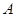 действует по формуле:
действует по формуле:
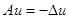 (7)
(7)
Формула интегрирования по частям и формулы Грина
При рассмотрении вариационных методов широко используются следующие соотношения.
Для функций 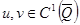 в
в 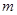 – мерной области
– мерной области 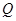 с кусочно-гладкой границей
с кусочно-гладкой границей 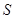 (
( 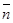 - вектор внешней нормали к поверхности
- вектор внешней нормали к поверхности 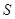 ) справедлива формула интегрирования по частям:
) справедлива формула интегрирования по частям:
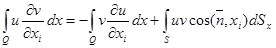 (8)
(8)
Рассмотрим далее дифференциальный оператор:
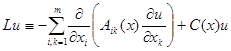 (9)
(9)
Первая формула Грина
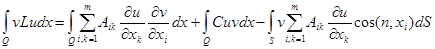 (10)
(10)
Вторая формула Грина
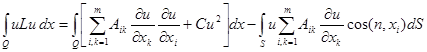 (11)
(11)
Третья формула Грина
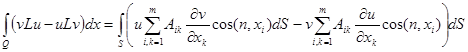 (12)
(12)
Соответствующие формулы Грина для оператора Лапласа
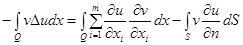 (10`)
(10`)
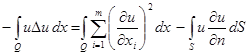 (11`)
(11`)
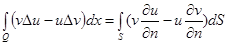 (12`)
(12`)
|
из
5.00
|
Обсуждение в статье: Краевая задача и ее оператор |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

