Применение собственных элементов сходного оператора.

Понятие о невязке

Если дано уравнение

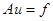                 (1)

и 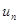 - какое-либо его приближенное решение, то разность  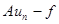называется невязкой этого приближенного решения. Пусть  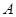- положительно определенный оператор, действующий в гильбертовом пространстве 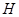, и 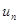 - приближенное решение уравнения (1) по Ритцу. Будем считать, что координатные элементы принадлежат области  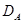определения оператора 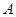, тогда  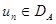и выражение  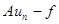- невязка – имеет смысл. В случае ограниченного оператора невязка стремится к нулю:

.

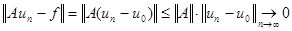При некотором специальном выборе координатной системы невязка также может стремиться к нулю.

Сходные операторы

Самосопряженные положительно определенные операторы 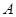 и 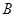, действующие в одном и том же гильбертовом пространстве, называются сходными, если .

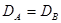Теорема о невязке

Пусть 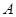 и 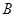 - сходные положительно определенные операторы, действующие в сепарабельном гильбертовом пространстве 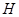, и пусть оператор  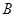имеет дискретный спектр. Если систему  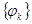собственных элементов оператора  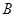принять за координатную для уравнения (1) и если

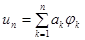         (2)

есть 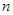-е приближение по Ритцу к точному решению уравнения (1), то невязка  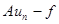стремится к нулю при .

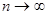Примеры сходных операторов

	Краевые условия			Дополнительные условия
1.	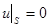.	.	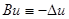.	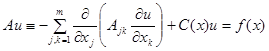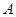- невырожденный оператор
2.	.	, .	.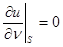

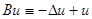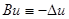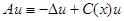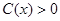
Решение методом Ритца краевых задач для обыкновенных дифференциальных уравнений

Рассмотрим краевую задачу

,

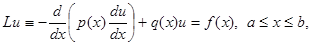
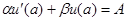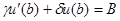
при условиях:

,   .

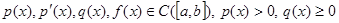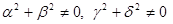Граничные условия определяют выбор последовательности координатных функций.

1. 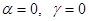, т.е. граничные условия имеют вид 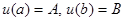. Приближенное решение ищется в виде:

,

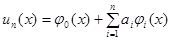где 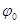 - любая достаточно гладкая функция, удовлетворяющая заданным граничным условиям, например 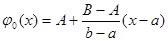. Координатные функции  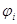- любые достаточно гладкие линейно независимые функции, удовлетворяющие соответствующим однородным условиям 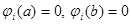. В качестве таких функций  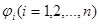можно взять функции

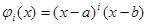
или

.

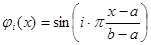2. В случае граничных условий 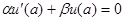,  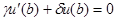можно взять в качестве координатных функции

,

,

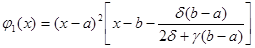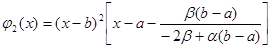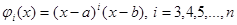
Ортонормирование по Шмидту

Пусть

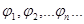,        (1)

- конечная или бесконечная последовательность элементов гильбертова пространства, и пусть при любом 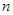 элементы  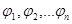линейно независимы. Положим

,                            .

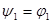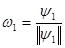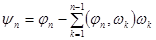
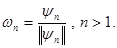
Последовательность 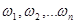 ортонормирована, при этом  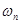линейно выражается через 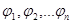, а 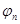 - линейно выражается через .

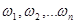Пример:

Провести ортогонализацию для базиса 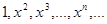 в случае интервала .

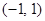Ответ: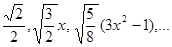

Вычисление скалярных произведений (A j_i, j_k) в случае уравнения для оператора

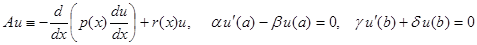(13)

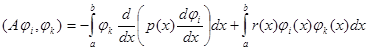
Если в первом интеграле провести интегрирование по частям, то получим эквивалентные соотношения:

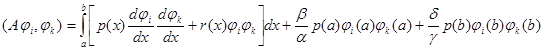
Возможный выбор базиса для оператора (13):

Граничные условия	Базис

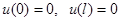
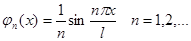
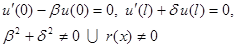
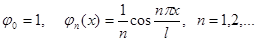
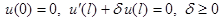
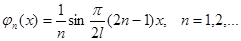
Метод Галеркина.

Рассмотрим H – сепарабельное гильбертово пространство, M – его плотное подмножество.

Известно, что если для некоторого u ÎH и "v Î M выполняется (u, v) = 0, тогда u = 0 в H.

Пусть {j _k} – базис в H, k = 1, 2, ¼Тогда если (u, j _k) = 0, k = 1, 2, ¼ то опять u = 0 в H. 

По нашему предположению {j _k} образует базис в H , тогда множество N всех элементов вида

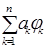                                                      (14)

( n – произвольное целое положительное число, a_k – произвольные вещественные числа ) является плотным в H . А так как для всех k выполняется (u, j _k) = 0, то

(u, 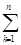a_k j _k) = 0

для всех элементов (14) из N ,откуда следует (13).

Пусть Аu = f – уравнение в H.

Если мы найдем элемент u₀Î D_A такой, что выполняется условие:

(Au₀ – f, j _k) = 0 " k = 1, 2, ¼,                           (15)

то из (13) следует, что

Au₀ – f = 0 в H ,                                                   (16)

т.е. u₀Î D_A – решение уравнения Аu = f в H.

Это рассуждение, ведущее к утверждению, что из (15) следует (16), составляет идею метода Галёркина.

Пусть базис {j _k} и область определения D_A оператора A таковы, что любая линейная комбинация (14) элементов этого базиса принадлежит D_A , и пусть приближенное решение u_n уравнения Аu = f ищется в виде

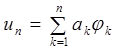,                                          (17)

где n – произвольное, но фиксированное число, а a_k – пока неизвестные постоянные. В методе Галёркина эти постоянные определяются из условий

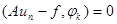, " k = 1, 2, ¼,n,                    (18)

аналогичных (15). Условия (18) представляют собой n уравнений для n неизвестных постоянных a₁, …, a_n.

Преобразуем 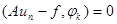, k = 1, 2, ¼ ,n (подставив (17):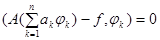

Если оператор A линеен, то условия (18) принимают вид

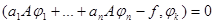, k = 1,…, n,                                       (19)

Если оператор A ещё и положителен (и поэтому симметричен), то систему (19) можно записать в виде

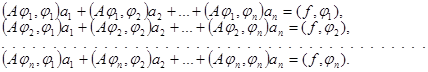      (20)

которая совпадает по форме с системой (12), полученной с помощью метода Ритца. Таким образом, выполнение предположений, необходимых для сходимости метода Ритца, означает также выполнение предположений, необходимых для сходимости метода Галёркина.

Замечание. В случае положительно определённых операторов метод Галёркина не дает ничего нового по сравнению с методом Ритца; эти два метода ведут к решению одинаковых систем линейных уравнений и к одинаковым последовательностям приближенных решений. Однако возможности применения метода Галёркина существенно шире, чем у метода Ритца. В методе Галёркина, характеризуемом условием (18), заранее не налагается на оператор A никаких существенных ограничений: не является необходимым, чтобы оператор A был положительно определенным, а тем более симметричным, но самое главное то, что он может быть нелинейным. Поэтому метод Галёркина может применяться даже в случае очень общих операторов.