Положительные и положительно определенные операторы

Симметричный оператор 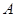 называется положительным, если для

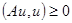         (1)

причем 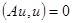 выполняется тогда и только тогда, когда .

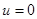Пример 1: , , .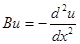

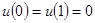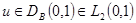Докажем, что оператор 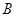положителен.

а)    симметричность

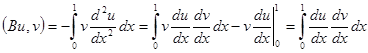
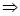
б)       

    

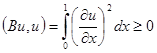
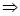
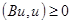
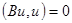
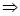
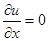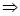
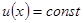
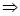
Если ,  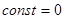(в соответствии с условиями на границе).

Пример 2: , , .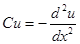

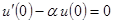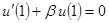а)    симметричность

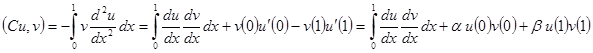
б) 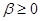  , 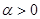. Докажем, что оператор С – положительно определенный

.

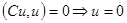
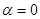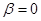, . Докажем, что оператор  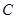не является положительно определенным

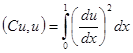. Если 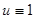, то 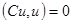 (не выполняется определение, хотя граничные условия выполняются).

Пример 3: , ,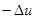

 

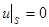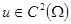
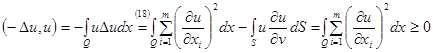
Рассмотрим задачу определения прогиба мембраны, закрепленной по краям:

,  

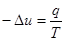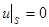
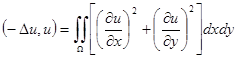 – пропорционально потенциальной энергии мембраны.

Потенциальная энергия мембраны, изогнутой как угодно, положительна, иначе говоря, невозможно изогнуть мембрану, не затратив на это энергии.

Пусть некоторая физическая система под действием внешней причины 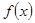, приобретает смещение  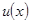и пусть

,

где 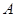 – положительный оператор. Тогда величина  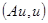пропорциональна величине энергии, которую необходимо затратить, чтобы сообщить системе смещение .

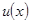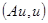 – энергия функции  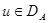(для положительного оператора ).

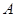Симметричный оператор 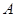 называется положительно определенным, если для  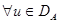справедливо неравенство

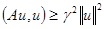                (11)

где 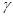 – положительная постоянная.

Если оператор положительно определенный, то он положительный, обратное не всегда верно.

 

Пример 4: , .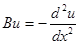

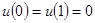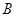 – положительный оператор. Докажем его положительную определенность.

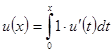 (с учетом )

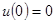Неравенство Буняковского: 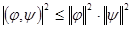. Примем , :

.

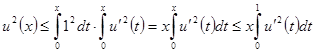
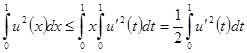
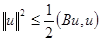
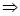
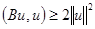 Энергетическое пространство положительно определенного оператора

Оператор 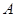 - положительно определенный оператор,  – линеал (область определения линейного оператора). Введем 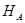 – энергетическое пространство оператора  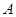(полное гильбертово пространство, совпадающее с 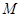) с обозначениями:

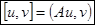.                                         (1)  - энергетическое произведение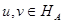

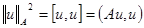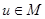,                 (4)  - энергетическая норма .

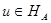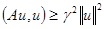.                                       (5)

 

Теорема 1.

Все элементы пространства 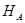 принадлежат также к пространству .

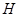(Точнее: каждому элементу из 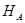 можно привести в соответствие один и только один элемент из 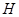, причем разным элементам из  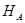соответствуют разные элементы из .)

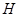Сходимость в энергетическом пространстве – сходимость по энергии ( ).

Теорема 2.

Если 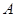 – положительно определенный оператор и  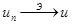по энергии, то одновременно  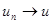в метрике исходного пространства :

 

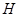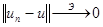
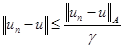
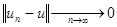
 Энергетическое пространство только положительного оператора

Оператор положительный, но не положительно определенный, называется только положительным. Не все элементы энергетического пространства только положительного оператора принадлежат исходному пространству.

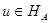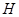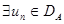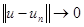Элемент  принадлежит исходному пространству  тогда и только тогда, когда , что  и 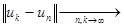0. При этом последовательность  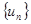стремится к тому же элементу 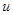в пространстве :

.

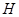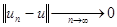Теорема.

Для того, чтобы энергетическое пространство положительного оператора было сепарабельным, необходимо и достаточно, чтобы было сепарабельным исходное гильбертово пространство.     

(Сепарабельное пространство - плотное, счетное, 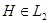 – сепарабельное пространство).

Итак:

Положительный оператор :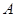

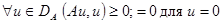
Положительно определенный оператор 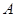:  , что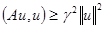

 Главные и естественные краевые условия

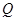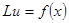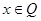, , ,                         (1)

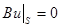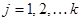,                             (2)

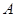 – оператор задачи (1), (2) в пространстве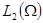

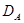 – множество функций из  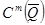и удовлетворяет (2) (  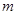–порядок уравнения (1)).

Пусть 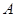 – положительный оператор,  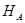– энергетическое пространство. Краевые условия, которым обязательно удовлетворяют функции из области определения оператора и необязательно – функции из энергетического пространства 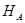, называются естественными для дифференциального оператора 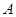. Краевые условия, которым обязательно удовлетворяют функции из энергетического пространства – главные условия.

1) 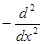, , 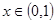,  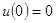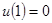– главные (геометрические, кинематические)

2) 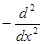, , 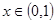,  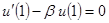– естественные (динамические)

Пример 5

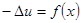          (3)

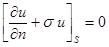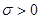,                           (4)

Докажем, что для уравнения (3) краевое условие (4) – естественное.

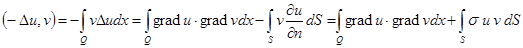 – симметрично относительно , .

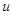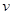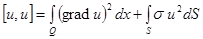 – имеет смысл  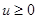для любых 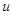, необязательно удовлетворяющих (3).

Построим функционал .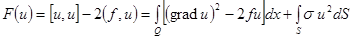

Покажем, что точное решение задачи (3), (4) 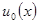 – реализует 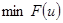. Используем принцип виртуальных перемещений  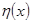с параметром .

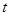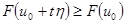 – имеет  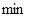при 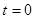 и фиксированном .

.

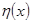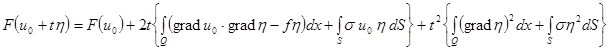При 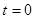 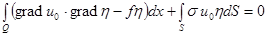                      (5)

По формуле Грина

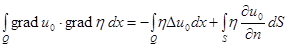
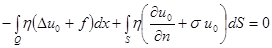, для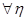

,        ,

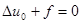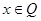
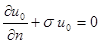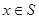
Метод Ритца.

Пусть 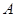 – положительно определенный оператор на линеале  в сепарабельном пространстве 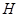, и 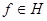. Пусть  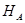– гильбертово пространство. Рассмотрим в  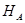базис 

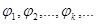.                                           (1)

Обобщенное решение уравнения 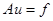 – это элемент 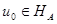, который минимизирует в  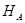функционал

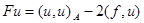,                                    (2)

т.е. элемент 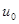, для которого

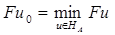                                   .                                     (3)

Выберем целое положительное число 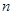, и будем искать аппроксимацию  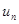элемента  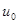в виде

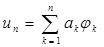,                                              (4)

где 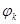 элементы базиса (1) , а  – неизвестные пока вещественные постоянные. Эти постоянные определяются из условия

Fu_n = min,                                                        (5)

которое означает, что среди всех аппроксимаций вида

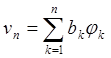,                                       (6)

где b_k – произвольные вещественные постоянные (т.е. в n-мерном подпространстве, порождаемом элементами j₁, …, j_k,), функционал F принимает минимальное значение в точности на аппроксимации (4). По предположению, (1) образует базис в H_A , так что обобщенное решение u₀можно с произвольной точностью аппроксимировать соответствующей линейной комбинацией его элементов. Кроме того, условие (5) аналогично (3). Поэтому приближение (4) с постоянными, определенными в соответствии с (5), будет достаточно мало отличаться от искомого решения u₀ в H_A, если n будет достаточно велико.

Постоянные b_k в (4) определяются подстановкой (6) вместо u в (2):

F v_n = (b₁ j₁ +…+ b_n j _n, b₁j₁ +…+ b_n j _n)_A – 2(f, b₁j₁ +…+ b_n j _n)=     

=(j₁, j₁)_A b₁² + (j₁, j₂)_A b₁ b₂ +…+ (j₁, j _n)_A b₁ b_n +            

+(j₂, j₁)_A b₂ b₁ + (j₂, j₂)_A b₂² +…+ (j₂, j _n)_A b₂ b_n +…              

+(j _n, j₁)_A b_n b₁ + (j _n, j₂)_A b_n b₂ +…+ (j _n, j _n)_A b_n²–              

–2(f, j₁) b₁ – 2(f, j₂) b₂ –…– 2(f, j _n) b_n ,         (7)

а с учетом симметрии скалярного произведения:

F v_n =(j₁, j₁)_A b₁² + 2(j₁, j₂)_A b₁ b₂ +…+ 2(j₁, j _n)_A b₁ b_n +                        

+ (j₂, j₂)_A b₂² +…+ 2(j₂, j _n)_A b₂ b_n +…+ (j _n, j _n)_A b_n²–             

– 2(f, j₁)b₁ – 2(f, j₂)b₂ –…– 2(f, j _n)b_n .                       (8)

Скалярные произведения (j _i,, j_k)_A – это фиксированные числа, определяемые элементами заданного базиса. Следовательно, в результате подстановки функционал F становится квадратичной функцией переменных b₁,…,b_n. Необходимые условия существования минимума этой функции в точке (a₁,…,a_n) есть:

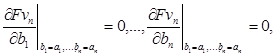                (9)

т.е. должны выполняться равенства

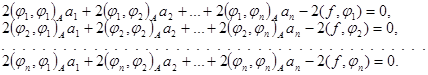      (10)

После простых преобразований эти уравнения можно записать в виде

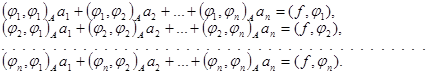      (11)

Система (11) – это система n уравнений для n искомых постоянных a₁,…,a_n. Так как по предположению j₁,…,j_n линейно независимы и определитель системы (11), являющийся определителем Грама, отличен от нуля, то существует единственное решение системы(11).

Замечание. Базис в H_A можно выбрать из элементов линеала D_A, так как это множество плотно в H_A. Тогда мы имеем (j _i, j_k)_A = (A j _i, j_k) для всех i, k=1,…,n,и систему (11) можно записать в виде

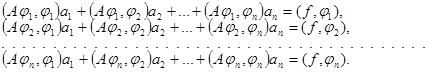(12)