Метод наименьших квадратов

Рассмотрим оператор A, положительно определенный на линеале D_A , который является плотным в сепарабельном гильбертовом пространстве H, и уравнение

Аu = f,

где f Î H . Пусть j₁, j₂,…,j _k Î D_A , k = 1, 2,… образуют базис в H, т.е. такую последовательность, что A j₁, A j₂,… образуют базис в H . Следовательно, для любого fÎH  и любого h> 0 можно найти положительное целое число m и постоянные c₁,…,c_m, что

,

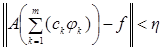или для линейного оператора :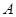

.

Метод наименьших квадратов состоит в нахождении приближенного решения u_n уравнения Аu = f  в виде

,                              (22)

где постоянные a_k определяются из условия

.                                    (23)

Если в (23) вместо  подставить сумму (22), то выражение(23) станет квадратичной функцией переменных . Необходимым условием минимума квадрата нормы является удовлетворение в точке (a₁,…, a_n) равенств

.

Аналогично методу Ритца, получим систему

(25)

Система (25) имеет единственное решение, поскольку ее определитель представляет собой определитель Грама, соответствующий первым n элементам последовательности (21), а эти элементы по предположению образуют базис в H , так что они линейно независимы в H .

 Метод Куранта.

Метод Куранта представляет собой некоторое сочетание метода Ритца и метода наименьших квадратов. Пусть заранее известно, что обобщенное решение  уравнения  принадлежит . Построим функционал

(1)

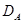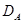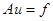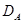где . Функционал  достигает минимума на  в точности на , поскольку  минимально на  в точности при  в соответствии с теоремой о минимуме квадратичного функционала;  так же минимально при , так как при этом . Таким образом, нахождение решения уравнения  эквивалентно нахождению элемента , минимизирующего в  функционал . Из формы функционала  видно, что его минимизация в 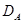 (например с помощью метода Ритца) труднее, чем минимизация исходного функционала  или . В тоже время метод Куранта сочетает преимущества метода Ритца и метода наименьших квадратов, и это положительно влияет на скорость сходимости решения.

В случае функционала (1) система уравнений для нахождения коэффициентов в приближении решения  приводится к виду

    (2)

Если мы строим минимизирующую последовательность для , например с помощью метода Ритца, то, очевидно, будем иметь сходимость в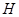

при .                        (2)

Если  и если известно, что как , так и  – достаточно гладкие в 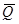 функции, то вместо функционала  можно рассматривать функционал

                        (3)

В этом случае вычисления, ведущие к нахождению  (например, по методу Ритца), будут более трудоемкими, но с другой стороны, сходимость последовательности  – очень быстрой. В частности из соотношений

            (4)

которые аналогичны соотношению (2), можно сделать выводы, касающиеся равномерной сходимости не только последовательности , но также и ее производных в рассматриваемой области.

 

 Метод Л.В.Канторовича приведения к обыкновенным дифференциальным уравнениям.

Найти решение уравнения (1)для положительного на 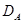 оператора  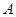с краевыми условиями (2)

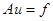                   (1)

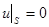                    (2)

Граница  области  представляет собой криволинейную трапецию, заданную соотношениями

.                         (3)

Решение задачи сведем к поиску минимума функционала:

                 (4)

Приближенное решение  будем искать в виде

, (5)

где  - заданные функции, удовлетворяющие условиям:

,  , ,    ,    (6)

а  – неизвестные функции, которые необходимо определить из условия минимума функционала (4). В качестве функций  можно брать, например, такие функции, удовлетворяющие условию (6)

1) 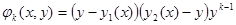,           2) .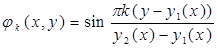

Подставим (5) в (4) , тогда

,

Если оператор 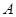 является дифференциальным оператором 2-ого порядка, то выражение под знаком интеграла преобразуется к виду

.

Выполняя интегрирование по переменной y, получим

,                   (7)

где  – известная функция своих аргументов. Для отыскания  решаем вариационную задачу о минимуме однократного интеграла.

Выписывая систему уравнений Эйлера

,  

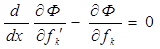и присоединяя краевые условия

,  ,

получим краевую задачу для системы линейных дифференциальных уравнений второго порядка, решая которую найдем , , а следовательно и .

Встречные методы

 Метод Трефтца.

Метод Трефтца позволяет оценивать снизу минимальное значение функционала энергетического метода. В методе Ритца приближенное решение ищется в классе функций, удовлетворяющих краевым условиям, но не удовлетворяющих дифференциальному уравнению. В противоположность этому в методе Трефтца приближенное решение ищется в классе функций, удовлетворяющих уравнению, но не удовлетворяющих краевому условию.

Рассмотрим краевую задачу (1),(2) для конечной области  с границей :

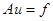                   (1)

                    (2)

Обозначим через  решение уравнения (1), и пусть  – линейно независимые решения соответствующего однородного уравнения, т. е.

(3)

Тогда линейная комбинация

                               (4)

будет снова решением уравнения (1): . Требуется так подобрать коэффициенты , чтобы функция  в каком-то смысле наиболее точно удовлетворяла граничным условиям (2). Например, можно подобрать  так, чтобы интеграл

                                (5)

принимал наименьшее значение. В этом случае для отыскания  получим систему линейных алгебраических уравнений

               (6)

Пусть  - точное решение задачи (1)–(2). Обозначим  - разность между приближенным и точным решением задачи. В методе Трефтца для решения задачи от  требуется, чтобы  обращала в минимум функционал .

В качестве примера рассмотрим следующую задачу:

,              .

Соответствующий функционал принимает вид

          (7)

т. е.  подбирают так, чтобы обращалась в минимум функция

                  (8)

Следовательно,  должны являться решением системы (9):

Этот интеграл нужно преобразовать так, чтобы неизвестное решение  в нем отсутствовало. Используя формулу Гаусса-Остроградского можно провести преобразования:

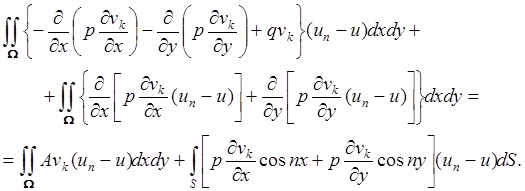(2.2.10)

Так как Av_k = 0, а u|_S = 0, то систему (2.2.9) можно переписать в виде

            (2.2.11)

В эту систему u(x, y) уже не входит. Решая ее, находим a₁,a₂,…,a_n , а следовательно и u_n(x, y).

Отметим, что если u_n(x, y) – приближенное решение краевой задачи, полученное по методу Треффтца, а u(x, y) – точное решение, то имеет место неравенство

F(u_n) £ F(u) = m,      где F(u) = (Au, u) - 2(u, f ),

т. е. метод Треффтца дает приближение к m снизу.

 Метод ортогональных проекций.

Будем искать функцию u(P), которая внутри конечной области W удовлетворяет уравнению Пуассона

– Du = f (P),                                                (2.1.1)

а на границе S области W – краевому условию

u|_S = 0.                                                    (2.1.2)

Для определенности будем считать, что функция f (P) имеет конечную норму, а W – двумерная область, так что

.

Формула из векторного анализа Du = div grad u позволяет записать уравнение (2.1.1) в виде

– div grad u = f (P).

Обозначим grad u = v. Наша задача будет решена, если мы найдем вектор v , так как восстановление функции по ее градиенту – дело достаточно простое. Теперь задачу можно сформулировать так : требуется найти вектор v(P), который удовлетворяет уравнению

– div v = f (P)                                             (2.1.3)

и представляет собой градиент некоторой скалярной функции, равной нулю на S.

Введем в рассмотрение пространство векторных функций, в котором скалярное произведение и норма определены формулами

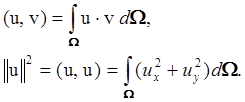
Для краткости обозначим это пространство через Ђ. Введем в Ђ два подпространства, которые обозначим через Ђ₁ и Ђ₂ . За Ђ₁ примем подпространство векторов, которые являются градиентами скалярных функций, равных нулю на S , за Ђ₂ — подпространство векторов, удовлетворяющих уравнению

div v = 0.

Дальнейшее основано на важной формуле

Ђ = Ђ₁ Å Ђ₂.

Эта формула содержит два утверждения:

1) Если вектор v₁ есть градиент некоторого скаляра, равного нулю на S, а вектор v₂ имеет дивергенцию, равную нулю, то эти векторы ортогональны в том смысле, что

2) Всякий вектор с конечной нормой можно представить в виде суммы двух векторов, из которых один есть градиент скаляра, равного нулю на S , а другой имеет равную нулю дивергенцию.

 

Теперь перейдем к изложению метода ортогональных проекций. Построим какой-либо вектор V(P), удовлетворяющий уравнению (2.1.3).

Положим V = v + w , где v – искомый вектор. Тогда

div w = div V – div v = 0,

так что w Î Ђ₂ . В то же время по условию задачи v Î Ђ₁ . Теперь ясно, что искомый вектор есть проекция вектора V на подпространство Ђ₁ – в этом и состоит метод ортогональных проекций.

Для построения проекции w выберем последовательность векторов y_i(P), удовлетворяющих уравнению div y_i = 0; если эта последовательность ортонормированна и полна в Ђ₂ , то

и решение нашей задачи дается формулой

                                     (2.1.4)

Проведем некоторый анализ формулы (2.1.4). Перепишем ее в виде

                   (2.1.5)

Все слагаемые справа (2.1.5) ортогональны: векторы y_n(P) ортогональны по условию, кроме того, v(P) и y_n(P) ортогональны, так как они принадлежат ортогональным подпространствам Ђ₁ и Ђ₂ . По свойствам ортогональности получим

                        (2.1.6)

Если в ряде (2.1.6) сохранить только конечное число m первых членов то правая часть равенства увеличится, и мы получим

                                (2.1.7)

Это соответствует замене точного решения (2.1.4) приближенным по формуле

По определению нормы векторной функции

Обозначая через u₀(P) функцию удовлетворяющую уравнениям (2.1.1) и (2.1.2), имеем v = grad u₀ и

                                   (2.1.8)

С другой стороны

                                                (2.1.9)

где F(u) = (–Du, u) - 2(u, f ) – функционал, используемый в энергетическом методе. Теперь из формул (3.1.7)–(3.1.9) следует

                              (2.1.10)

Теперь мы видим, что метод ортогональных проекций позволяет оценить снизу погрешность приближенного решения, построенного по методу Ритца.

Список литературы

1. Березин Н.С., Жидков Н.П. Методы вычислений, 2 том, М.: Физматгиз, 1962. 640с

2. Гавурин М.К.Лекции по методам вычислений. М. Наука.1971, 248с

3. Демидович Б.П., Марон И.А., Шувалова Э.З. Численные методы анализа. М.: Физматгиз, 1962. 368с

4. Митчелл Э., Уэйт Р. Метод конечных элементов для уравнений с частными производными. М. Мир, 1981. 216с.

5. Михайлов В.П. Дифференциальные уравнения в частных производных. М.: Наука, 1983.- 424 с

6. Михлин С.Г. Вариационные методы в математической физике. М. Наука.1970, 512с

7. Михлин С.Г. Численная реализация вариационных методов. М. Наука.1966, 432с

8. Ректорис К. Вариационные методы в математической физике и технике. М, Мир, 1985. 590с

9. Сегерлинд Л. Применение метода конечных элементов. М, Мир, 1979. 392с

10. Шуп Т. Решение инженерных задач на ЭВМ. М.: Мир, 1982.- 238 с.

11. Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление. М. Наука.1969, 424с