Модель популяции с наименьшей критической численностью

В рассмотренных моделях прирост численности (биомассы) популяции представлен линейным членом, пропорциональным численности. Строго говоря, это соответствует лишь тем популяциям, размножение которых происходит путем самооплодотворения (микроорганизмы). Если же в основе размножения лежит скрещивание, предполагающее встречи между особями разных полов одного и того же вида, то прирост будет тем выше, чем больше количество встреч между особями, а последнее пропорционально второй степени N. [4] Таким образом, для разнополой популяции в условиях неограниченных ресурсов можно записать:

=r×               (8)

Уравнение (8) хорошо описывает тот факт, что при низких плотностях популяций скорость размножения резко падает, так как вероятность встречи двух особей разных полов уменьшается при понижении плотности популяции пропорционально квадрату плотности. Однако при больших плотностях популяций скорость размножения лимитирует уже не число встреч особей противоположного пола, а число половозрелых самок в популяции. Кроме того, важно учесть время, в течение которого может состояться оплодотворение. Если это время больше времени, в течение которого особь способна к размножению, то популяция вымирает.

Пусть Т – среднее время между двумя последующими оплодотворениями, τ – среднее время вынашивания плода, постоянное для каждого вида, t_ср – среднее время, в течение которого может состояться оплодотворение:

t_ср = Т – τ. Вероятность встречи, ведущей к оплодотворению, тем больше, чем больше соотношение t_ср/Т. Тогда коэффициент размножения для разнополых популяций r, можно представить в виде:

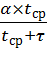= ,                  (9)

где α – коэффициент пропорциональности, t_ср – величина, уменьшающаяся при возрастании плотности популяции:t_ср = β/N, β = const.

Тогда,

Таким образом, уравнение, учитывающее фактор разнополости и количество самок, готовых к оплодотворению, имеет вид:

                           (10)

Графики численности в зависимости от времени (рис. 1 а) и скорости размножения как функции численности (рис. 1б) для уравнения (10) представлены на рис. 1.
В действительности плотность популяции не должна опускаться ниже некоторой критической величины. При падении плотности популяции ниже критической среднее время, в течение которого может состояться оплодотворение, становится больше времени жизни отдельной особи, точнее, времени, в течение которого особь способна к размножению. В этом случае популяция вымирает.[5]

Рис. 1. а - график зависимости численности от времени и б - скорости размножения как функции численности для уравнения (10)

Этот эффект может быть учтен, если в формулу (10) ввести член, пропорциональный численности популяции с коэффициентом γи описывающий смертность. Зависимость скорости роста популяции от ее численности при этом примет вид:

                      (11)

Уравнение (11) имеет два стационарных решения: ₁=0 и ₂=  (значения параметров модели задаются такими, чтобы величина L была положительной).

Исследуем устойчивость стационарных состояний графическим методом. Для этого необходимо определить знак функции:

Знаменатель функции положителен при положительных значениях N, меняет знак при прохождении через значение N = - β/τ. Числитель меняет знак при прохождении через стационарные точки _1,2 .В результате имеем при N > ₂ = L, в области 0 <N < L функция (рис. 1 а). При прохождении через точку ₁=0 скорость роста популяции модели (11) меняет знак с «плюса» на «минус», что означает устойчивость стационарного состояния ₁. При прохождении точки ₂  скорость роста меняет знак с «минуса» на «плюс», что позволяет сделать вывод о неустойчивости этого стационарного состояния.

В случае, когда начальная численность популяции лежит в пределах от 0 до L, скорость ее роста отрицательна, т.е. популяция вымирает. Если же начальная численность больше L – популяция неограниченно растет. Величина Lполучила название нижняя критическая численность (плотность). График зависимости численности популяции, описываемый моделью (11) от времени представлен на рис. 2 б.

Рис. 2. Модель популяции с наименьшей критической численностью. Зависимости скорости роста популяции от ее размера (а) и динамика численности популяции (б).

Величина нижней критической плотности L различна для разных видов. Наблюдения биологов показали, что это всего лишь одна пара особей на тысячу квадратных километров в случае ондатр и сотни тысяч особей для американского странствующего голубя. Заранее трудно было предугадать, что столь многочисленный вид перешел через критическую границу своей численности и обречен на вырождение. Однако это произошло, несмотря на все усилия по охране этих птиц.

Для голубых китов критическая граница общей численности оказалась равной десяткам - сотням. Хищническое истребление этих гигантских животных привело к тому, что их осталось слишком мало в Мировом океане. И хотя охота на них запрещена, надежд на восстановление популяции голубых китов практически нет.

Учтем в модели (11) важный фактор внутривидовой конкуренции. В этом случае получим общий закон, описывающий динамику разнополой популяции в условии ограничения ресурсов:

              (12)

Данное нелинейное уравнение, обладающее «триггерными» свойствами, в 1985 г. предложил А.Д.Базыкин. [6]

Уравнение имеет три стационарных значения:

.

Это нулевое решение ₁=0, а также два значения, обращающих в ноль квадратный трехчлен: ₂= L’ и ₃ = K’.Значения численности L’ и K’ являются критическими: ₂ = L – минимально возможная численность, ₃ = K’ – максимально возможная (параметры модели α,β, τ, γ, δ выбирают такими, чтобы величины L’ и K’ были положительными). Устойчивость стационарных состояний проверим, аналогично предыдущему случаю, графическим методом. Функция модели (12) в положительной области значений переменной N меняет знак с «плюса» на «минус» при переходе через ₁=0 (это стационарное состояние устойчиво), затем с «минуса» на «плюс» в точке ₂ = L’ (неустойчивое стационарное значение) и, наконец, опять с «плюса» на «минус» в точке ₃ = K’(устойчивое стационарное значение) (рис.3 а). График зависимости численности популяции, описываемый моделью (12) от времени представлен на рис. 3 б.

Рис. 3. Модель популяции с нижней и верхней критическими границами численности. Зависимость скорости роста популяции от ее размера (а) и динамика численности популяции (б).

При любых промыслах особый интерес представляет величина нижней критической границы, при переходе через которую популяция уже не сможет восстановиться. Модель позволяет дать некий методический рецепт определения не самой критической границы, но степени близости к ней численности вида.
Обратимся к рис. 3 б. Пусть численность вида в начальный момент времени была близка к максимально возможной. При t = 0 происходит одноразовое выбивание популяции. Если численность осталась значительно больше критической, восстановление происходит сначала быстро, а затем с монотонным замедлением (кривая 1). Если же оставшаяся популяция близка к критической точке, восстановление происходит сначала очень медленно, численность популяции надолго "застревает" вблизи критической точки, а затем уже, "набрав силы", более быстро приближается к стационарному уровню (кривая 2). Таким образом, наблюдая реакцию системы на возмущение, можно предсказать приближение ее к опасным границам.

Заключение.

Математические модели - не только средство для количественного описания явлений. Модель сложной системы - это математический образ, позволяющий формализовать и обобщить в терминах теории представления о многочисленных свойствах и характеристиках сложной системы. Расширение понятийного и образного круга не меньше чем количественные расчеты представляет собой ценный результат междисциплинарных исследований с применением аппарата математики и физики для изучения живых систем. В этом смысле популяционная динамика занимает особое место. При всей ограниченности "числа особей", как характеристики вида или сообщества, значение термина "численность" имеет четкий и универсальный смысл.

Описанная математическая модель популяции с наименьшей критической численностью имеет огромную практическую ценность, так как помогает определить, в каком состоянии (устойчивом или нет) будет находиться популяция в определенный промежуток времени, а также позволяет предсказать приближение размера популяции к опасным границам, дальше которых идет вырождение. 

Список литературы.

1. http://lww-infproekt0405.narod.ru/Modeli_11/Mod_biol.htm

2. http://mialo.narod.ru/ped/models/popul.htm

3. В. Д. Мятлев, Л. А. Панченко, Г. Ю. Ризниченко, А. Т. Терехин Теория вероятностей и математическая статистика. Математические модели. М., Академия, 2009, 320 с.

4. Ризниченко Г. Ю. Лекции по математическим моделям в биологии.

5. http://www.biophys.msu.ru/

6. А.Д.Базыкин. Математическая биофизика взаимодействующих популяций. М., Наука, 1985, 165 с.