Инфляционный рост суммы S при годовом уровне инфляции a подобен наращению суммы S по сложной годовой ставке процентов a .

 

Через год сумма S’_a будет больше суммы S в (1+a) раз. По прошествии ещё одного года S”_a будет больше суммы S’_a в (1+a) раз, т.е. больше суммы S в (1+a)² раз.

Через n лет сумма Sⁿ_a=S(1+a)ⁿ

Т.е.

 

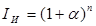Теперь, на основании изученных в предыдущих параграфах формул, необходимо выяснить, как влияет инфляция на величину процентной ставки и будущую сумму при разных методах начисления процентов.

 

Если в обычном случае первоначальная сумма P при заданной ставке процентов превращается за определённый период в сумму S, то в условиях инфляции для сохранения покупательной способности на том же уровне она должна превратиться в сумму S_a, что требует уже иной процентной ставки.

Такая ставка называется – ставка, учитывающая инфляцию.

 

Тогда, используя предыдущие обозначения, принимается:

i _a - ставка ссудного процента, учитывающая инфляцию;

d _a - учётная ставка, учитывающая инфляцию;

j _a - номинальная ставка сложного процента, учитывающая инфляцию;

и т.д.

 

Если задать годовой уровень инфляции a и простую годовую ставку ссудного процента i . Тогда для наращенной суммы S, превращающейся в условиях инфляции в S_a, используется формула:

 

Для данной суммы ещё можно записать следующее соотношение:

 

Для этих двух формул можно составить уравнение эквивалентности:

 

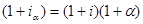Из этого уравнения следует, что

 

Эта формула называется формулой И. Фишера. В ней сумма a+i a - величина, которую нужно прибавить к реальной ставке доходности для компенсации инфляционных потерь. Эта величина называется инфляционной премией.

Применение формулы Фишера для различных способов начисления процента за несколько лет позволяет определить ставки с учётом инфляции. При этом всегда удобно пользоваться значением индекса инфляции за весь рассматриваемый период (I_И).

 

Простая декурсивная ставка:

 

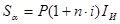Уравнение эквивалентности:

 

Отсюда:

Аналогично находится простая антисипативная ставка, учитывающая инфляцию:

 

Сложная декурсивная ставка:

 

 

 

Если начисление процентов происходит несколько раз в год (m раз), то для определения номинальной ставки, учитывающей инфляцию, имеем:

 

Отсюда:

 

Таким же образом получаем формулы для случая сложных учётных ставок:

 

Используя полученные формулы, можно находить процентную ставку, компенсирующую потери от инфляции, когда заданы процентная ставка, обеспечивающая желаемую доходность финансовой операции, и уровень инфляции в течение рассматриваемого периода.

Можно получить формулы, позволяющие определить реальную доходность финансовой операции, когда задан уровень инфляции и ставка процентов, учитывающая инфляцию.

Например, для сложной декурсивной ставки:

 

 

Подставив в последнюю формулу вместо индекса инфляции выражение (1+a)ⁿ, получим формулу:

 

Из этой формулы видно:

· если i_{c a} = a (доходность и уровень инфляции равны), то i_c =0, т.е. весь доход поглощается инфляцией;

· если i_{c a} < a (доходность вложений ниже уровня инфляции), то i_c <0, т.е. операция приносит убыток;

· если i_{c a} > a (доходность вложений выше уровня инфляции), то i_c >0, т.е. происходит реальный прирост вложенного капитала.

 

 

Аннуитеты

 

В большинстве современных коммерческих операций подразумеваются не разовые платежи, а последовательность денежных поступлений (или, наоборот, выплат) в течение определенного периода.

Это может быть серия доходов и расходов некоторого предприятия, выплата задолженностей, регулярные или нерегулярные взносы для создания разного рода фондов и т. д. Такая последовательность называется потоком платежей.

Поток однонаправленных платежей с равными интервалами между последовательными платежами в течение определенного количества лет называется аннуитетом (финансовой рентой).

Теория аннуитетов является важнейшей частью финансовой математики. Она применяется при рассмотрении вопросов доходности ценных бумаг, в инвестиционном анализе и т.д.

Наиболее распространенные примеры аннуитета: регулярные взносы в пенсионный фонд, погашение долгосрочного кредита, выплата процентов по ценным бумагам.

Аннуитеты различаются между собой следующими основными характеристиками:

· величиной каждого отдельного платежа;

· интервалом времени между двумя последовательными платежами (периодом аннуитета);

· сроком от начала аннуитета до конца его последнего периода (бывают и неограниченные по времени — вечные аннуитеты);

· процентной ставкой, применяемой при наращении или дисконтировании платежей.

Аннуитеты классифицируются по сроку платежей:

· аннуитет, для которого платежи осуществляются в начале соответствующих интервалов, носит название пренумерандо;

· если же платежи осуществляются в конце интервалов, мы получаем аннуитет постнумерандо (обыкновенный аннуитет) -пожалуй, самый распространенный случай.

 

Наибольший интерес с практической точки зрения представляют аннуитеты, в которых все платежи равны между собой (постоянные аннуитеты), либо изменяются в соответствии с некоторой закономерностью.

Такие аннуитеты и рассматриваются в рамках курса «Управление финансами». Подробное изучение других аннуитетов – прерогатива специализированных дисциплин.

Введем следующие обозначения:

Р –  величина каждого отдельного платежа;

i_c — сложная процентная ставка, по которой начисляются проценты;

S_k— наращенная сумма для k-го платежа аннуитета постнумерандо;

S — наращенная (будущая) сумма всего аннуитета постнумерандо (т. е. сумма всех платежей с процентами);

A_k — современная величина k-го платежа аннуитета постнумерандо;

А — современная величина всего аннуитета постнумерандо (т. е. сумма современных величин всех платежей);

S_П — наращенная сумма аннуитета пренумерандо;

А_П — современная величина аннуитета пренумерандо;

п — число платежей.

 

Рассмотрим аннуитет постнумерандо с ежегодными платежами Р в течение п лет, на которые начисляются проценты по сложной годовой ставке i_c,.

Рис.3 Будущая стоимость аннуитета постнумерандо

 

Сумма S ₁ для первого платежа, проценты на который будут начисляться, очевидно, (n-1) раз, составит по формуле сложной декурсивной ставки:

 

 

Для второго платежа (проценты на него будут начисляться на один год меньше) имеем:

 

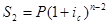и так далее. На последний платеж, произведенный в конце n-го года, проценты уже не начисляются, т. е.

 

Тогда для общей наращенной суммы имеем:

 

 

где k_{i , n} — коэффициент наращения аннуитета с параметрами i, п.

 

Он представляет собой сумму членов геометрической прогрессии, для которой первый член а₁ равен 1, а знаменатель (q) составляет (1+i_c).

Используя математическую формулу для суммы членов геометрической прогрессии:

 

 

запишем выражение в более удобном для вычислений виде:

 

Для коэффициента наращения, соответственно, имеем:

 

 

Современная величина А данного аннуитета определяется следующим образом.

 

Рис. 4 Современная величина аннуитета постнумсрандо

 

При заданной процентной ставке i_c современное значение каждого платежа будет определяться по формуле:

 

Это вытекает из рисунка.

Современная величина всего аннуитета, следовательно, составит:

 

где а _{i , n} — коэффициент приведения аннуитета с параметрами i , n.

Это выражение опять является суммой геометрической прогрессии, теперь уже с параметрами а₁= q =1/(1+ i_c ).

Получается выражение для современной величины А:

 

Из выражений для расчёта будущей и современной величины аннуитета очевидно, что они связаны между собой выражением:

 

 

Из полученных формул путём преобразования можно получить формулы для расчёта очередного платежа (Р) или срока аннуитета (п).

 

Для аннуитета пренумерандо с теми же параметрами расчёт аналогичен.

 

Рис.5. Будущая стоимость аннуитета пренумерандо

 

Очевидно, отличие от предыдущего случая состоит здесь в том, что период начисления процентов на каждый платеж увеличивается на один год, т. е. каждая наращенная сумма S_k увеличивается в (1+i_c) раз. Следовательно, для всей суммы S _П имеем:

 

Для коэффициента наращения аннуитета пренумерандо:

 

Для определения современных значений каждого платежа дисконтирование по заданной ставке i_c проводится на один раз меньше, чем в случае аннуитета пренумерандо. Поэтому каждая современная величина A_k будет больше в (1+i_c) раз.

Таким образом:

 

А для коэффициента приведения получаем:

 

Если срок аннуитета п не ограничен, мы получаем случай вечного аннуитета. Для аннуитета постнумерандо выражения для наращенной суммы не будет иметь экономического смысла, а современная величина будет рассчитываться следующим образом:

 

Для аннуитета пренумерандо, соответственно:

 

 

Таким образом, различие между двумя типами вечных аннуитетов, естественно, сказывается на определении их современной величины.

 

Ещё один важный вопрос при изучении потоков платежей — конверсия аннуитетов.

Под конверсией аннуитета понимается такое изменение начальных параметров аннуитета, после которого новый аннуитет был бы эквивалентен данному.

Два аннуитета считаются эквивалентными, если равны их современные величины, приведенные к одному и тому же моменту времени.

На практике необходимость рассчитать параметры эквивалентного аннуитета чаще всего возникает при изменении условий выплаты долга, погашения кредита или займа и т. п. При этом конверсия может произойти как в момент начала аннуитета (на этот момент и рассчитываются современные величины эквивалентных аннуитетов), так и после выплаты некоторой части аннуитета. В последнем случае все расчеты производятся на остаток долга в момент конверсии.

Наиболее распространенные случаи конверсии постоянных аннуитетов:

1. Через некоторый промежуток времени n ₀ (он может быть равен и 0) после начала аннуитета весь остаток долга может быть выплачен за один раз (выкуп аннуитета). Очевидно, что в этом случае величина выплачиваемой суммы будет равна современной величине остатка аннуитета, рассчитанной для срока п₁ = п — п₀.

2. Может возникнуть задача, обратная предыдущей: задолженность погашается частями, в виде выплаты постоянного аннуитета, и требуется определить один из параметров аннуитета при заданных остальных. Поскольку здесь известна сумма долга, т. е. современная величина аннуитета, с помощью формул, рассмотренных выше, находим неизвестный параметр.

3. Период выплаты долга может быть изменен при сохранении прежней процентной ставки. Величину Р₁ платежа для срока п₁ находим, используя уравнения эквивалентности (приравниваются современные значения аннуитетов).

Очевидно, что, если срок аннуитета увеличится, значение Р сократится, и наоборот.

4. В некоторых случаях может потребоваться объединение нескольких аннуитетов в один (консолидация аннуитетов). При этом объединяемые аннуитеты могут быть любыми, а в искомом объединяющем аннуитете один из параметров неизвестен при всех остальных занятых.

Могут встречаться и другие случаи применения конверсии аннуитетов.