Различные способы приведения квадратичных форм к каноническому виду и к нормальному виду.

Приведение квадратичной формы к каноническому виду методом Лагранжа.

Пусть дана квадратичная форма f ( x )=а(х,х). Вслед­ствие формулы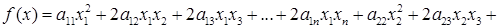

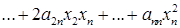
 мы можем в любом базисе записать f ( x ) в виде

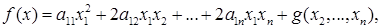                                  (1)

где g — квадратичная форма, не включающая x ₁ .

Запись вида (1) позволяет доказать возможность приве­дения квадратичной формы к каноническому виду по индук­ции.

Теорема. Каждую квадратичную форму с помощью невырожденного линейного преобразования можно привести к каноническому виду.

Замечание. Здесь речь идет о преобразовании пере­менных, именно числовых аргументов х₁,...,х_п многочлена (1). Но теорему можно понимать и геометрически, поскольку всякое невырожденное преобразование переменных можно рассматривать как преобразование координат при переходе к новому базису.

Доказательство теоремы. Квадратичная форма от одного переменного всегда имеет канонический вид 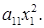 Примем как предположение индукции, что любую квадра­тичную форму от (n—1) числовых аргументов можно при­вести к каноническому виду невырожденным линейным пре­образованием (n—1) переменных.

Рассмотрим произвольную квадратичную форму f ( x ) от nчисловых аргументов:

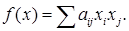
Пользуясь предположением индукции, докажем, что ее можно привести к каноническому виду невырожденным линейным преобразованием n переменных. Возможны два случая:

1) Первый случай. В квадратичной форме хотя f ( x ) хотябы один из коэффициентов а _ij при квадратах переменных отличен от нуля. Не нарушая общности, можем считать, что

именно а₁₁≠ 0. По данным коэффициентам формы f ( x ) coставим следующее линейное преобразование:

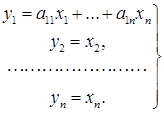                                                         (2)

Матрицу этого преобразования обозначим Q:

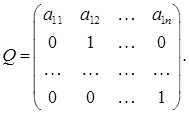
Преобразование (2) невырождено, так как Det Q = a₁₁ ≠ 0 . Отметим также, что невырожденность преобразования (2) вы­текает из его обратимости, которая в свою очередь сразу видна из формул (2).

Возведем в квадрат выражение y ₁ и разделим на a₁₁ ≠0:

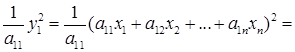
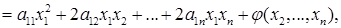
где 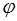— некоторая квадратичная форма аргументов х_2,...,х_п, т. е.  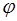 не включает x₁. Введем еще одну квадратичную фор­му  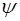тех же аргументов х₂,..., х_п, положив

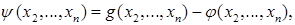
где g { x ₂ ,..., х_п) дана записью f ( x ) в виде (1). Тогда по­лучим

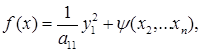
или, что то же самое,

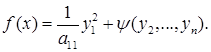
По предположению индукции существует такое невырож­денное преобразование переменных в числе п—1

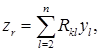
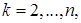                                                              (3)

которое приводит к каноническому виду форму :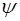 

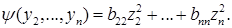
Дополним преобразование (3) так, чтобы в нем участво­вали все п переменных. Именно, положим

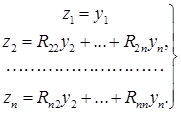                                                                          (4)

Преобразуем переменные x ₁ ..., x_n в переменные  у₁,... ...,у_п по формулам (2), а затем переменные y₁,…,у_п преобра­зуем по формулам (4). В результате получим преобразование переменных х₁..., х_п в переменные z₁,..., z_n которое при­водит исходную квадратичную форму к каноническому виду

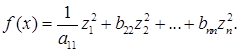
Последнее преобразование является невырожденным, так как представляет собой произведение невырожденных преобразо­ваний (2) и (4).

Второй случай. В квадратичной форме f ( x ) все, диагональные коэффициенты а _ii равны нулю. Тогда преды­дущие рассуждения неприменимы. Но какой-нибудь из коэф­фициентов отличен от нуля; пусть это будет а₁₂. Тогда квад­ратичная форма имеет вид

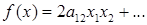                                                                         (5)

Сделаем преобразование:

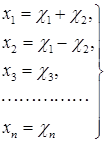                                                                                (6)

Преобразование (6) обратимо и, следовательно, является не­вырожденным.

Подставив величины (6) в квадратичную форму (5), по­лучим

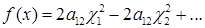                                                                     (7)

Слагаемое 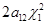 не может исчезнуть при приведении подобных членов, так как все члены квадратичной формы, которые не выписаны в выражении (5), не содержат произве­дения  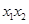и не могут в результате преобразования (6) дать величину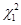

Далее квадратичную форму (7) можно невырожденным преобразованием привести к каноническому виду, поскольку дело свелось к первому случаю: коэффициент при 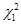 отличен от нуля.

Тем самым рассуждения индукции завершены и теорема доказана.

3 а м е ч а н и е. Из доказательства видно, что квадра­тичную форму с действительными коэффициентами можно привести к каноническому виду с помощью невырожденного линейного преобразования, которое также имеет действитель­ные коэффициенты.

Приведение квадратичной формы к каноническому виду методом Якоби.

Пусть дана квадратичная форма f ( x ), которая расписана в координатах в некотором базисе е₁,…, е_п:

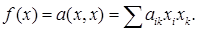
Как известно,

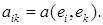
Составим матрицу квадратичной формы f ( x ):

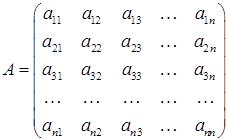
Рассмотрим так называемые главные миноры матрицы А:

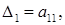
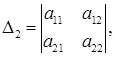
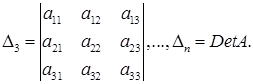                                                   (1)

Кроме того, для удобства записи дальнейших формул введем величину 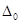считая 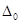=1.

Метод Якоби проходит в предположении, что все главные миноры матрицы А отличны от нуля:

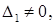
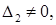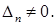                                      …                          (2)

При этих предположениях ищется специальный новый базис такой, чтобы

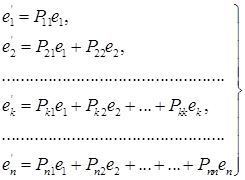                                                      (3)

Для того чтобы привести квадратичную форму f ( x ) к каноническому виду, достаточно для любого 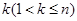 обеспечить условия

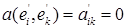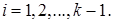                              при                   (4)

Тогда 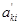 тоже будут равны нулю (вследствие симметрич­ности матрицы квадратичной формы), и отличными от нуля окажутся лишь коэффициенты при квадратах числовых аргу­ментов.

Заметим, что для выполнения условий (4) достаточно потребовать соблюдения равенств

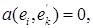
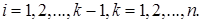                                              (5)

В самом деле, из (5) и (3) имеем

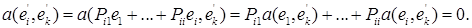
Для упрощения дальнейших выводов добавим к (5) дополни­тельное равенство

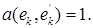                                                                                    (6)

При k = 1 условия (5) исчезают и остается только (6), из которого, с учетом первой строчки формул (3), находим

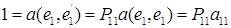
Отсюда

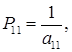
 поскольку .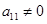

Учитывая обозначения (1), можно написать

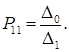
Дальше будем проводить рассуждение по индукции. Допустим, что уже определены все коэффициенты, входящие в первые k—1 строк формул (3). Для нахождения коэффи­циентов, входящих в строку с номером k , запишем условия (5), и (6) вместе

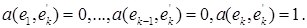                                                 (7)

Отсюда, используя (3), получим для искомых коэффициентов систему уравнений

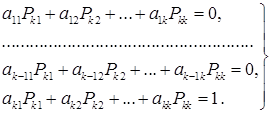                                                      (7а)

Определитель системы (7а) совпадает с 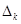и отличен от нуля вследствие предположения (2). Поэтому искомые коэффи­циенты Р _{k 1} , ..., Р _kk найдутся. Остается проверить, что по­строенное преобразование невырождено. С этой целью найдем из системы (7а) коэффициент P_kk . Применяя правило Крамера, получим

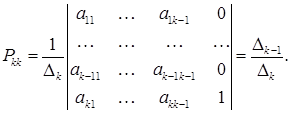                                                    (8)

Далее, используя треугольную структуру матрицы преобразо­вания (3), найдем определитель D этой матрицы:

.

Таким образом, 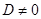, а значит, преобразование (3) невы­рождено.

Теперь мы можем определить и коэффициенты квадра­тичной формы в новом базисе 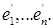 Достаточно вычис­лить лишь диагональные коэффициенты, так как осталь­ные заведомо равны нулю. Используя (3), (7) и (8), на­ходим

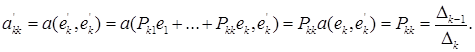
Значит, в базисе, который построен по методу Якоби,

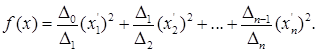
  Приведение квадратичных форм к нормальному виду.

Пусть квадратичная форма f ( x ) приведена к канониче­скому виду

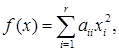                                                                                       (1)

где а₁₁,..., а _r ≠ 0, r — ранг f ( x ).

Допустим, что мы имеем дело с комплексным прост­ранством и разрешаем себе пользоваться  линейными

преобразованиями с комплексными коэффициентами. Положим

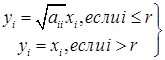                                                                             (2)

Из (1) и (2) получим

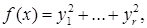                                                                                 (3)

считая, что у₁,..., у _r , у r +1,. .., у_п— новые координаты век­тора х. Выражение (3) называется нормальным видом квад­ратичной формы f ( x ). Заметив, что преобразование (2) невы­рождено, сделаем вывод:

В комплексном пространстве всякую квадратичную форму можно с помощью невырожденного линейного пре­образования привести к нормальному виду (3).