Положительно-определённая квадратичная форма

Определение 1. Форма f ( x ) называется положительно определенной, если f ( x ) > 0 для всех .

Заметим, что  всегда. В самом деле, так как =0*z и f ( x ) = а (х, х), где z — произвольный вектор, а (х, у) — билинейная функция, то

Квадратичная форма f ( x ) называется отрицательно определенной, если f ( x )<0 для любого .

Очевидно, что достаточно рассмотреть положительно опре­деленные формы, поскольку отрицательно определенные полу­чаются из них сменой знака.

Ограничиваясь квадратичными формами в конечномер­ных (n-мерных) пространствах, укажем прежде всего ряд простых необходимых признаков положительной определен­ности. Пусть в каком-нибудь базисе е₁ .,., е_п дана квадра­тичная форма

Как нам известно,

1) Если f ( x ) является положительно определенной, то  при всех i =1,2, ..., п.

2) Если форма f ( x ) положительно определена, то опре­делитель ее матрицы положителен:

Для доказательства приведем f ( x ) к каноническому виду. Пусть  — канонический базис, то есть базис, в кото­ром f ( x ) имеет канонический вид:

Согласно предыдущему признаку все

Обозначим через  определитель матрицы формы f ( x ) в каноническом базисе. Имеем

С другой стороны

значит,

Замечание. И это условие не является достаточным для положительной определенности квадратичной формы. Пример: форма

имеет  однако

3) В n-мерном пространстве каждая положительно опре­деленная форма имеет ранг п. Доказательство вытекает из неравенства

Теорема (критерий Сильвестра). Для положитель­ной определенности квадратичной формы необходимо и достаточно, чтобы все главные миноры ее матрицы были положительны.

Доказательство необходимости. Пусть форма f { x ) положительно определена. Возьмем произвольный базис 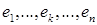построим линейную оболочку Будем теперь рассматривать квадратичную форму f { x ) не на вcём пространстве, а лишь на подпространстве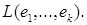

Если то  и

Все остальные члены, у коэффициентов которых хотя бы один из двух индексов больше k , исчезают за счет нулевых значений координат.

Форма f ( x ) на подпространстве является по­ложительно определенной, так как она положительно опре­делена на всем пространстве. Поэтому определитель формы f ( x ), рассматриваемой на  положителен:

Но — главный минор порядка k матрицы квадратичной формы f ( x ), индекс k может принимать значения 1, 2,..., п. Тем самым необходимость признака доказана.

Доказательство достаточности. Пусть  при k = 1,..., п.

Приведем квадратичную форму к каноническому виду методом Якоби. Получим

Бели , то хотя бы одна из координат , и, следо­вательно, . Теорема доказана.

Обратим внимание на двумерный случай. Пусть

где на этот раз числовые аргументы формы обозначены через х, у.

Условие Сильвестра сводится к неравенствам

Разумеется, в двумерном случае теорему Сильвестра можно установить без какой-либо специальной теории, поскольку для положительной определенности необходимо a > 0 и при а > 0

Приложение 1

Пример 1. Дана квадратичная форма . Привести её к каноническому виду.

Решение. Составим характеристическое уравнение

или . Корни этого уравнения . Собственные векторы, определяющие главные направления квадратичной формы найдём из системы:

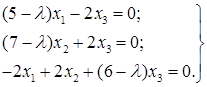                                                             (1)

Подставляя сюда поочередно значения  и беря каждый раз нормированное решение системы (1), получаем:

Формулы преобразования координат при переходе к этому базису:

В базисе  квадратичная форма имеет канонический вид

Пример 2. Привести к каноническому виду квадратичную форму

Решение. Составим уравнение

или . Отсюда . Канонический вид данной квадратичной формы

Для того чтобы найти базис, в котором форма имеет вид, необходима найти собственные векторы симметрического линейного преобразования с матрицей

Запишем систему уравнений, определяющую искомые собственные векторы:

                                                                     (1)

Подставляя сюда  и беря каждый раз нормированное решение системы (1), найдем векторы, определяющие главные направления квадратичной формы:

Они составляют нужный базис.

При переходе к базису  координаты всех векторов преобразуются по формулам:

Пример 3. Найти для квадратичной формы

её матрицу.

Решение. Для данной квадратичной формы запишем

 

Следовательно её матрица равна

.

Пример 4. Подвергнем форму  преобразованию

Мы получили форму

Подвергая её обратному преобразованию

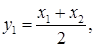
 приходим к исходной форме

Пример 5. С помощью линейных преобразований переменных преобразуем квадратичную форму  в канонический вид.

После преобразования

Перейдёт в форму с матрицей

т.е в форму

Квадратная матрица вида

у которой все элементы вне главной диагонали равны нулю, называется диагональной (канонической) матрицей.  

Приложение 2

Список используемой литературы

1. Александров П. С., Лекции по аналитической геомет­рии, пополненные необходимыми сведениями из алгебры, «Наука», 1968.

2. Ефимов Н. В., Линейная алгебра и многомерная геометрия, «Мир», 1961

3. Боревич З.И., Определители и матрицы, «Наука», 1986

4. Гантмахер Ф.Р., Теория матриц, «Дрофа», 2001

5. Шилов Г. Е., Математический анализ. Конечномерные линейные пространства, «Наука», 1969