 |
Главная |
Формулы преобразования и матрицы преобразования.
|
из
5.00
|
Переход от одной аффинной системы координат к другой с тем же началом. Аффинная координатная система, или аффинный репер о пространстве, есть тройка некомпланарных векторов 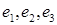 данных в определенном порядке и приложенных к точке О — началу репера.
данных в определенном порядке и приложенных к точке О — началу репера.
Тройка векторов 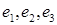 называется иногда базисом репера или координатной системы.
называется иногда базисом репера или координатной системы.
Если наряду с репером  который будем условно называть «старым», дан «новый» репер с началом О' и базисом
который будем условно называть «старым», дан «новый» репер с началом О' и базисом 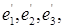 то возникает общая задача преобразования координат: по координатам произвольной точки М (произвольного вектора u) в одной из двух систем координат найти координаты той же Точки (того же вектора) в другой системе.
то возникает общая задача преобразования координат: по координатам произвольной точки М (произвольного вектора u) в одной из двух систем координат найти координаты той же Точки (того же вектора) в другой системе.
Предположим, что оба репера имеют одно и то же начало О. Тогда новый репер вполне определен, если заданы векторы  своими координатами (относительно старого базиса), т. е. если даны коэффициенты
своими координатами (относительно старого базиса), т. е. если даны коэффициенты 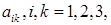 в равенствах
в равенствах
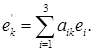 (1)
(1)
Матрица

называется матрицей перехода от базиса 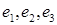 к базису
к базису  а также матрицей перехода от первого репера ко второму. Так как векторы
а также матрицей перехода от первого репера ко второму. Так как векторы 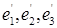 линейно независимы, то детерминант матрицы А* отличен от нуля — матрица перехода от одного базиса к другому есть всегда невырожденная матрица. Так как векторы
линейно независимы, то детерминант матрицы А* отличен от нуля — матрица перехода от одного базиса к другому есть всегда невырожденная матрица. Так как векторы  образуют базис, то каждый из векторов
образуют базис, то каждый из векторов 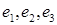 в свою очередь однозначно представим как линейная комбинация векторов
в свою очередь однозначно представим как линейная комбинация векторов 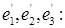
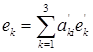 (1’)
(1’)
- уравнения (1) однозначно разрешимы относительно старых единичных векторов 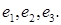
Посмотрим, как связаны между собой координаты x , у, г и х', у', г' произвольной точки М (произвольного вектора u = ОМ) в старой и новой координатных системах.
Вектор и=ОМ записывается, во-первых, как линейная комбинация векторов  с коэффициентами х, у, г и, во-вторых, как линейная комбинация векторов
с коэффициентами х, у, г и, во-вторых, как линейная комбинация векторов 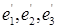 с коэффициентами х', у', г', так что имеем тождество
с коэффициентами х', у', г', так что имеем тождество

Вносим в это тождество выражения  из (1); получаем
из (1); получаем
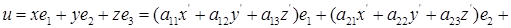
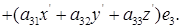
Но вектор u единственным образом представляется как линейная комбинация векторов  , следовательно, коэффициенты при векторах
, следовательно, коэффициенты при векторах  в левой и правой частях последнего равенства должны быть одни и те же, т. е.
в левой и правой частях последнего равенства должны быть одни и те же, т. е.
 (2)
(2)
Эти формулы и выражают старые координаты х, у, г точки М (вектора u ) через новые. Матрица
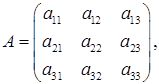 (3)
(3)
дающая это выражение, называется матрицей преобразования координат; она является транспонированной по отношению к матрице А* перехода от базиса  к базису
к базису 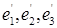 . Обе матрицы имеют один и тот же отличный от нуля детерминант.
. Обе матрицы имеют один и тот же отличный от нуля детерминант.
2. Переход от одной аффинной системы координат к другой с изменением начала координат. Общий случай перехода от репера  к реперу
к реперу 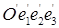 сводится к комбинации двух случаев переноса начала и только что разобранного случая перехода от одного базиса к другому. В самом деле, рассмотрим наряду с двумя реперами
сводится к комбинации двух случаев переноса начала и только что разобранного случая перехода от одного базиса к другому. В самом деле, рассмотрим наряду с двумя реперами  и
и  еще третий, «промежуточный», имеющий начало О' = ( x 0 , y 0 , z 0 ) и базис
еще третий, «промежуточный», имеющий начало О' = ( x 0 , y 0 , z 0 ) и базис 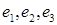 ; координаты точки относительно этого промежуточного репера обозначим через х", у", z ". Тогда х= x 0 + х", у= y 0 + у", z = z 0 + z ", где х", у", z " выражаются через х', у', z ' по формулам (2) (в которых, естественно, надо х, у, z (слева) соответственно заменить на х", у", z ". Получаем окончательно:
; координаты точки относительно этого промежуточного репера обозначим через х", у", z ". Тогда х= x 0 + х", у= y 0 + у", z = z 0 + z ", где х", у", z " выражаются через х', у', z ' по формулам (2) (в которых, естественно, надо х, у, z (слева) соответственно заменить на х", у", z ". Получаем окончательно:
в пространстве:
 (43)
(43)
на плоскости
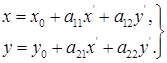 (42)
(42)
Это н есть общие формулы преобразования координат для двух произвольных аффинных координатных систем. Матрица

коэффициентов 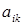 в равенствах (43) соответственно (42) называется матрицей преобразования координат.
в равенствах (43) соответственно (42) называется матрицей преобразования координат.
Переход от одной прямоугольной системы координат к другой
Случай прямоугольного репера на плоскости. Можно ограничиться реперами с общим началом. Базис прямоугольного репера состоит из двух взаимно перпендикулярных ортов. Такие базисы будем называть прямоугольными или ортонормальными.
Лемма. Пусть 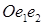 и
и 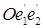 — два ортогональных репера на плоскости с общим началом О. Тогда поворотом репера
— два ортогональных репера на плоскости с общим началом О. Тогда поворотом репера 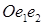 в несущей его плоскости вокруг точки О на некоторый угол
в несущей его плоскости вокруг точки О на некоторый угол  можно перевести репер
можно перевести репер 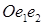 либо в репер
либо в репер 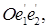 либо в репер
либо в репер 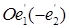 (рис. 59 и 60). Другими словами: репер
(рис. 59 и 60). Другими словами: репер  получается из репера
получается из репера  либо поворотом, либо поворотом и последующим отражением (относительно прямой, несущей вектор
либо поворотом, либо поворотом и последующим отражением (относительно прямой, несущей вектор 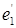 ).
).
Доказательство. Репер 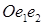 определяет некоторое положительное направление вращения плоскости, а именно то направление, в котором угол от ортаe1 до орта e2 равен
определяет некоторое положительное направление вращения плоскости, а именно то направление, в котором угол от ортаe1 до орта e2 равен  (а не
(а не  ).
).
Обозначим через  угол от орта e1 до орта е1’. Повернув репер
угол от орта e1 до орта е1’. Повернув репер  (в его плоскости) в положительном направлении на угол
(в его плоскости) в положительном направлении на угол  , мы совместим орт e1 с ортом е1’; тогда орт e2, будучи перпендикулярен к орту e1, либо совместится с ортом
, мы совместим орт e1 с ортом е1’; тогда орт e2, будучи перпендикулярен к орту e1, либо совместится с ортом  (рис. 59), либо
(рис. 59), либо
совместится с противоположным ему ортом —  (рис. 60). Утверждение доказано.
(рис. 60). Утверждение доказано.
Из доказанного следует, что относительно базиса e1 , e2 орт  имеет координаты cos
имеет координаты cos  , sin
, sin  :
:
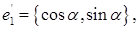
тогда как для  имеем две возможности:
имеем две возможности:
либо
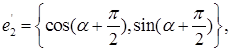
т.е
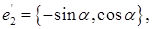
либо
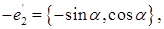
и тогда
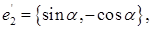
Матрица перехода от базиса 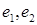 к базису
к базису 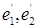 имеет вид:
имеет вид:
в первом случае
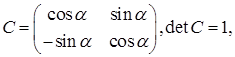 (I)
(I)
во втором
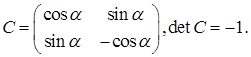 (II)
(II)
Базисы 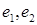 и
и 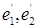 называются в первом случае одноименными или одинаково ориентированными, а во втором — разноименными или противоположно ориентированными.
называются в первом случае одноименными или одинаково ориентированными, а во втором — разноименными или противоположно ориентированными.
Так как detC = l в случае одноименных, detC= -1 в случае разноименных базисов, то только что высказанное определение можно сформулировать и так:
Определение. Два ортогональных базиса (репера) одно-именны, если матрица перехода от одного из них к другому имеет положительный детерминант, и разноименны, если этот детерминант отрицателен.
Формулы преобразования координат даются матрицами, транспонированными к матрицам перехода от одного базиса к другому; это будут формулы:
 в случае однименных базисов,
в случае однименных базисов,
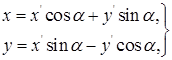 в случае разноименных базисов.
в случае разноименных базисов.
|
из
5.00
|
Обсуждение в статье: Формулы преобразования и матрицы преобразования. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

