 |
Главная |
Матрица квадратичных форм. Теорема о ранге матрицы
|
из
5.00
|
Теория
1.1 Введение. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
1.2 n-мерное векторное пространство. Преобразование . . . . . . . . . . . . . . . . . . 2
систем координат.
1.3 Определение квадратичных форм. Общий вид, . . . . . . . . . . . . . . . . . . . . . .4
канонический вид, нормальный вид.
1.4 Матрица квадратичнаых форм. Теорема о ранге матрицы.. . . . . . . . . . . . . 7
1.5 Различные способы приведения квадратичных форм к . . . . . . . . . . . . . . . .8
каноническому виду и к нормальному виду
1.6 Формулы преобразования и матрицы преобразования.. . . . . . . . . . . . . . . 14
1.7 Закон инерции квадратичных форм. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
1.8 Положительно-определённая квадратичная форма. . . . . . . . . . . . . . . .. . . 19
Приложения
2.1 Приложение 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
2.2Приложение 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
Введение
В данной работе мы рассмотрим квадратичные формы и основные операции над ними. А также в заключении моей работы решим пять задач по данной теме.
1.2 n -мерное векторное пространство. Преобразование систем координат.
Из правил сложения векторов и умножения вектора на число вытекают важные свойства, которые легко доказываются:
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4) 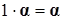 ;
;
5)  ; 6)
; 6)  ;
;
7) т×0 = 0; 8) если тa = 0, то или т = 0, или a = 0.
Совокупность всех п-мерных векторов, рассматриваемая с определёнными в ней операциями сложения векторов и умножения вектора на число, называется п-мерным векторным пространством.
Геометрический смысл сложения и умножения на число двумерных и трёхмерных векторов.
Вектор b называется линейной комбинацией векторов a1, a2, ¼, aп, если существуют такие числа т1, т2, ¼, т п, что
b = т1a1 + т2a2 ¼ + т пaп
Линейной оболочкой  системы векторов
системы векторов  называется множество всех линейных комбинаций этой системы векторов.
называется множество всех линейных комбинаций этой системы векторов.
Система векторов a1, a2, ¼, aп называется линейно зависимой, если найдутся такие числа т1, т2, ¼, т п, хотя бы одно из которых не равно нулю, что имеет место равенство
т1a1 + т2a2 ¼ + т пaп = 0.
Линейно независимая система п-мерных векторов
a1, a2,¼, a п (1)
называется максимальной линейно независимой системой, если добавление к ней любого п- мерного вектора b даёт линейно зависимую систему. Если (1) – максимальная линейно независимая система, то во всякой линейной комбинации векторов a1,a2,¼,a п,b, равной нулю, коэффициент при векторе b должен отличаться от нуля(!), и вектор b можно представить в виде линейной комбинации векторов a1, a2,¼, a п. Отсюда следует, что система пмерных векторов тогда и только тогда будет максимальной линейно независимой системой, если её векторы линейно независимы, а любой п-мерный вектор является линейной комбинацией этих векторов.
Теперь можно сделать заключение. В п-мерном пространстве всякая линейно независимая система, состоящая из п векторов, будет максимальной, а любая максимальная линейно независимая система векторов этого пространства состоит не более чем из п векторов.
Всякая линейно независимая система п-мерных векторов содержится хотя бы в одной максимальной линейно независимой системе. Действительно, если заданная система векторов не максимальна, то к ней можно присоединить один вектор так, что полученная система останется линейно независимой. Если новая система не максимальна, то к ней можно добавить ещё один вектор. Этот процесс может продолжаться до тех пор, пока в системе не будет п векторов.
Введём в геометрическом n-мерном пространстве произвольную систему и будем рассматривать переменные  как координаты точки М в этой системе. Тогда
как координаты точки М в этой системе. Тогда  есть значение квадратичной формы в точке М.
есть значение квадратичной формы в точке М.
Перейдём к новой системе координат по формулам:
 (2)
(2)
Здесь  - старые;
- старые;  - новые координаты одной и той же точки.
- новые координаты одной и той же точки.
Выясним, как изменится матрица квадратичной формы при переходе к новой системе координат. Запишем преобразование координат (2) в матричной форме
 (3)
(3)
Где X – матрица-столбец, составленная из старых координат; Y – матрица-столбец, составленная из новых координат; B – неособенная матрица с элементами. Подставив выражение (3) в равенство  , получим
, получим

Но, по правилу транспонирования произведения,  Следовательно,
Следовательно,
 (4)
(4)
Матрица  симметрична, так как
симметрична, так как  а Y – матрица-столбец, составленный из переменных
а Y – матрица-столбец, составленный из переменных  Поэтому выражение (4) является квадратичной формой от этих переменных. Её матрица равна
Поэтому выражение (4) является квадратичной формой от этих переменных. Её матрица равна  .
.
Таким образом, если в квадратичной форме с матрицей А перейти к новой системе координат, то в любых переменных квадратичная форма будет иметь матрицу  где B – матрица перехода.
где B – матрица перехода.

1.3 Определение квадратичных форм. Общий вид, канонический вид, нормальный вид.
Числовая функция а(х, у) двух векторных аргументов х, у называется билинейной, если она линейна по каждому аргументу, то есть




Здесь x, у, х1, х2, у1, у2—любые векторы пространства L , α —произвольное число.
Пусть L — линейное n-мерное пространство е1, ..., еп — базис в нем, и пусть аргументы билинейной функции разложены по этому базису:
 ,
,  .
.
Тогда
 (1)
(1)
Введем обозначения:
 (2)
(2)
Тогда получим
 (3)
(3)
Формула (3) выражает функцию а(х,у) в координатах по данному базису.
Многочлен в правой части формулы (3) называется билинейной формой. Вместе с ним билинейной формой называют и самую функцию а(х,у). Числа а ik называются коэффициентами данной формы в базисе е1, ..., еп. В качестве аргументов х, у можно рассматривать векторы как действительного, так и комплексного линейного пространства. Соответственно говорят, что форма а(х,у) дана в действительном или в комплексном пространстве. В последнем случае в качестве значений формы а(х, у) допускают комплексные числа; коэффициенты а ik этом случае также являются, вообще говоря, комплексными числами.
Пусть билинейная форма а(х,у) является симметричной: а(у,х)=а(х,у). Это равносильно тому, что в любом базисе симметрична ее матрица: А* = А. В самом деле,

Отождествим оба аргумента формы а(х,у). Тогда получим а(х,х) = а(х,у) при у = х.
Функция а(х, х) называется квадратичной формой, отвечающей данной симметричной билинейной форме а(х,у).
Исходная (симметричная) билинейная форма а(х, у) называется полярной для квадратичной формы а(х, х).
Докажем, что полярная билинейная форма однозначно определяется своей квадратичной формой.
Пусть дана числовая функция f ( x ) векторного аргумента. Предположим, что f { x ) есть некоторая квадратичная форма, т. е. f ( x ) = a ( x , x ), причем а{х,у) нам неизвестна. Чтобы найти ее, рассмотрим f ( x + y ), где х, у — произвольные векторы. Пользуясь свойствами билинейной формы и ее симметричностью, имеем


Отсюда получаем искомое выражение
 (4)
(4)
Формулу (4) можно принять за определение квадратичной формы. Именно можно сказать, что f ( x ) называется, квадратичной формой, если левая часть формулы (4) является билинейной функцией.
Следует заметить, что определение квадратичной формы не предусматривает наличия базиса; тем самым, оно применимов бесконечномерных пространствах.
Пример. Пусть L — линейное пространство функций, непрерывных на отрезке [0, 1].
Рассмотрим функцию

аргумент которой x = x ( t )ЄL .
Имеем
 (5)
(5)
Нетрудно непосредственно проверить, что в правой части равенства (5) стоит билинейная форма. Таким образом, f { x ) есть квадратичная форма в бесконечномерном пространстве L .
Вернемся к n-мерному случаю. В n-мерном пространстве рассмотрим квадратичную форму и запишем ее выражение через координаты аргументов.
Пусть а (х,у) = а (у, х), х=у. Тогда


……….…………………………
 (6)
(6)
Если принять во внимание симметричность коэффициентов, то члены суммы (6), кроме диагональных, естественно объединяются в пары. При этом получается часто употребляемая запись квадратичной формы в виде

 . (7)
. (7)
Заметим, что в первой строчке формулы (7) выписаны все члены, содержащие x 1 .
Ранг квадратичной формы по определению равен рангу ее матрицы: г = Rang A .
Канонический вид квадратичной формы. Если в некотором базисе окажется, что все коэффициенты aik = 0 при i ≠ k , то говорят, что в этом базисе квадратичная форма имеет канонический вид
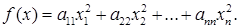
Приведение квадратичной формы к каноническому виду является важной задачей как в теоретических вопросах, так и в прикладной математике. Ниже рассмотрим два метода приведения квадратичной формы к каноническому виду: метод Лагранжа и метод Якоби.
Если Rang = r < n, то после надлежащего изменения номеров матрицу можно записать в виде
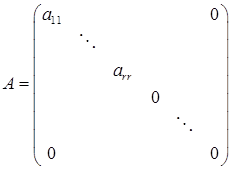 .
.
Замечание. Если привести к каноническому виду квадратичную форму, то одновременно приведется к диагональному виду и ее билинейная форма

Нормальный вид квадратичной формы
 (8)
(8)
считая, что у1,..., у r , у r +1,. .., уп— новые координаты вектора х. Выражение (8) называется нормальным видом квадратичной формы f ( x ).
В комплексном пространстве всякую квадратичную форму можно с помощью невырожденного линейного преобразования привести к нормальному виду (8).
Ограничимся теперь действительными пространствами и действительными линейными преобразованиями. Учитывая, что среди коэффициентов а ii могут быть отрицательные, положим
 (9)
(9)
Если первые k коэффициентов а ii положительны, а остальные отрицательны, то мы получим
 . (9*)
. (9*)
Выражение (9*) также называется нормальным видом формы f ( x ).
Матрица квадратичных форм. Теорема о ранге матрицы
Вся квадратичная форма может быть записана в виде


 (1)
(1)
…………………………………….

Ясно, что коэффициенты  формы
формы  в записи (1) определены одназначно. Составленная из них матрица
в записи (1) определены одназначно. Составленная из них матрица

Называется матрицей квадратичной формы 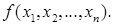 Ввиду
Ввиду  элементы матрицы A, расположенные симметрично относительно главной диагонали, равны между собой. Следовательно
элементы матрицы A, расположенные симметрично относительно главной диагонали, равны между собой. Следовательно  , т.е. A – симметричная матрица.
, т.е. A – симметричная матрица.
Очевидно, что для любой симметричной матрицы A всегда можно указать такую квадратичную форму, что её матрица совпадает с A. Если две квадратичные формы имеют одну и ту же матрицу, то эти формы могут отличаться друг от друга обозначением переменных, что не имеет существенного значения. Две такие квадратичные формы мы можем считать одинаковыми. Таким образом, квадратичные формы вполне определяются своими матрицами.
Теорема о ранге матрицы. Ранг произвольной матрицы равен максимальному порядку ее миноров, отличных от нуля.
Доказательство. Если Rang А = 0, то A — нулевая матрица, и у нее нет отличных от нуля миноров. Естественно считать в этом случае, что максимальный порядок отличных от нуля миноров равен нулю.
Пусть далее матрица А — не нулевая. Если некоторый ее минор М порядка rне равен нулю, а все миноры более высокого порядка равны нулю или отсутствуют вовсе, то М является базисным минором. По лемме о базисном миноре столбцы матрицы А, пересекающие минор М, линейно независимы. Поэтому Rang A ≥ r . По той же лемме любой столбец матрицы А линейно выражается через базисные столбцы. Отсюда, применяя лемму , находим, что Rang A ≤ r . Таким образом, Rang A = r , что и требовалось доказать.
|
из
5.00
|
Обсуждение в статье: Матрица квадратичных форм. Теорема о ранге матрицы |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

