 |
Главная |
Метод простой итерации
|
из
5.00
|
Заданная система
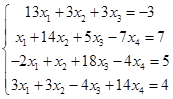
Метод Гаусса
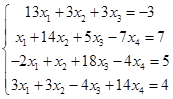 (1.1.)
(1.1.)
Прямой ход
Нормируем первое уравнение системы, разделив все члены уравнения на его первый коэффициент при 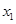 :
:
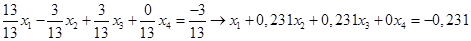 (1.2.)
(1.2.)
Умножим нормированное уравнение (1.2) на коэффициенты при х1 оставшихся уравнений системы (1.1).
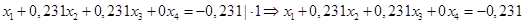 (1.3.)
(1.3.)
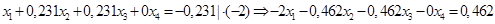 (1.4.)
(1.4.)
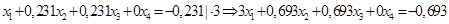 (1.5.)
(1.5.)
Вычтем полученные уравнения (1.3.), (1.4.), (1.5.) из второго, третьего и четвёртого уравнения системы (1.1.) соответственно, чтобы исключить из системы х1:
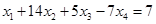
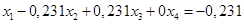 (1.6.)
(1.6.)
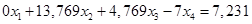
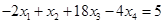
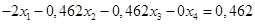 (1.7.)
(1.7.)
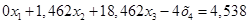
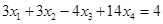
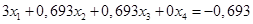 (1.8.)
(1.8.)
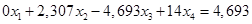
Получим новую систему уравнений:
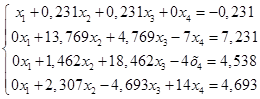 (1.9.)
(1.9.)
Рассмотрим систему уравнений (1.9).
Решим систему уравнений без первого уравнения системы (1.9.).
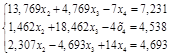 (1.10.)
(1.10.)
Нормируем первое уравнение системы (1.10.), разделив все члены уравнения на коэффициент при 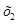 :
:
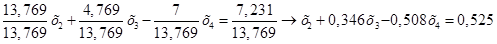 (1.11.)
(1.11.)
Умножаем нормированное уравнение (1.11.) на коэффициент при х2 оставшихся уравнений:
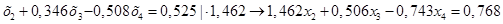 (1.12.)
(1.12.)
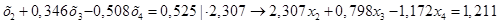 (1.13.)
(1.13.)
Вычтем полученные уравнения (1.12.), (1.13.) из второго и третьего уравнения системы (1.10.) соответственно, чтобы исключить из системы х2:
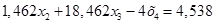
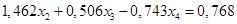 (1.14.)
(1.14.)
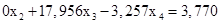
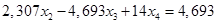
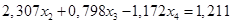 (1.15.)
(1.15.)
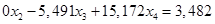
Получим новую систему уравнений:
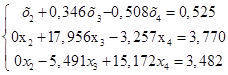 (1.16.)
(1.16.)
Рассмотрим систему (1.16) без первого уравнения:
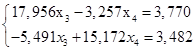 (1.17.)
(1.17.)
Нормируем первое уравнение системы (1.17.).
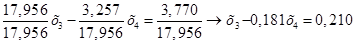 (1.18.)
(1.18.)
Умножаем полученное уравнение (1.18.) на коэффициент при х4 второго уравнения системы (1.17.):
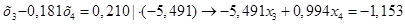 (1.19.)
(1.19.)
Вычтем полученное уравнение (1.19.) из второго уравнения системы (1.18.):
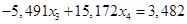
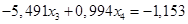 (1.20.)
(1.20.)
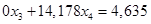
Получим новую систему линейных уравнений:
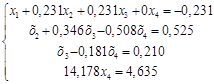 (1.21.)
(1.21.)
Рассмотрим последнее уравнение системы (1.21.).
Нормируем данное уравнение:
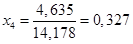 (1.22.)
(1.22.)
В результате выполненных действий система (1.1.) приведена к треугольному виду:
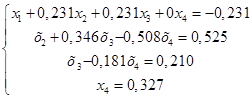 (1.23.)
(1.23.)
Обратный ход
x4 = 0,327;
Найдём 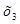 из третьего уравнения системы (1.23.):
из третьего уравнения системы (1.23.):
x3 = 0,210+0,181·0,327=0,269;
Найдём 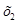 из второго уравнения системы (1.23.):
из второго уравнения системы (1.23.):
x2 = 0,525–0,346·0,269+0,508·0,327 = 0,598;
Найдём 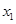 из первого уравнения системы (1.23.):
из первого уравнения системы (1.23.):
x1 = -0,231–0,231·0,598–0,231·0,269+0·0,327 = -0,431
Решением системы линейных уравнений являются значения неизвестных:
Ответ: x1 = -0,431;
x2 = 0,598;
x3 = 0,269;
x4 = 0,327.
Метод простой итерации
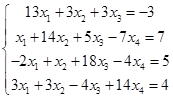
Выполним проверку на сходимость
|a11|>|a12|+|a13|+|a14| → |13|>|3|+|3|+|0|
|a22|>|a21|+|a23|+|a24| → |14|>|1|+|5|+|-7|
|a33|>|a31|+|a32|+|a34| → |18|>|-2|+|1|+|-4|
|a44|>|a41|+|a42|+|a43| → |14|>|3|+|3|+|-4|
Условия сходимости выполняются, следовательно, решение может быть найдено с определенной точностью за некоторое число итераций.
Вычислим значения неизвестных системы линейных алгебраических уравнений с точностью ε 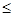 0,001.
0,001.
Примем за нулевое приближение неизвестных значения, равные нулю, т.е.
x1(0) = 0; x2(0) = 0; x3(0) = 0; x4(0) = 0;
Подставим полученные значения в итерационные формулы и вычислим значения неизвестных при первом приближении.
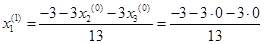 = -0,231
= -0,231
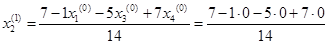 = 0,500
= 0,500
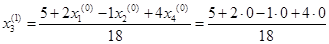 = 0,278
= 0,278
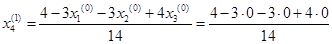 = 0,286
= 0,286
Выполним проверку полученных значений:
|x1(1)-x1(0)| = |-0,231–0| = 0,231 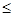 ε – нет
ε – нет
|x2(1)-x2(0)| = |0,500–0| = 0,500 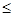 ε – нет
ε – нет
|x3(1)-x3(0)| = |0,278–0| = 0,278 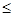 ε – нет
ε – нет
|x4(1)-x4(0)| = |0,286–0| = 0,286 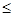 ε – нет
ε – нет
Выполним вторую итерацию.
Подставим значения неизвестных, полученные в первой итерации, в итерационные формулы и вычислим значения неизвестных при втором приближении.
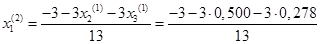 = -0,410
= -0,410
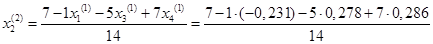 = 0,560
= 0,560
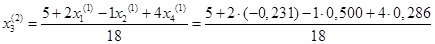 = 0,288
= 0,288
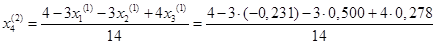 = 0,308
= 0,308
Выполним проверку полученных значений:
|x1(2)-x1(1)| = |-0,410+0,231| = 0,179 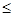 ε – нет,
ε – нет,
|x2(2)-x2(1)| = |0,560–0,500| = 0,060 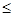 ε – нет,
ε – нет,
|x3(2)-x3(1)| = |0,288–0,278| = 0,010 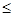 ε – нет,
ε – нет,
|x4(2)-x4(1)| = |0,308–0,286| = 0,022 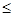 ε – нет.
ε – нет.
Выполним третью итерацию.
Подставим значения, полученные во втором приближении, в итерационные формулы и вычислим значения неизвестных при третьем приближении.
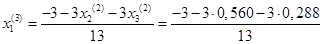 = -0,427
= -0,427
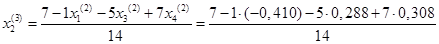 = 0,580
= 0,580
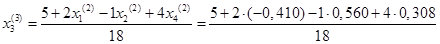 = 0,270
= 0,270
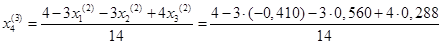 = 0,336
= 0,336
Выполним проверку полученных значений:
|x1(3)-x1(2)| = |-0,427+0,410| = 0,017 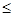 ε – нет,
ε – нет,
|x2(3)-x2(2)| = |0,580+0,560| = 0,020 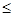 ε – нет,
ε – нет,
|x3(3)-x3(2)| = |0,270–0,288| = 0,018 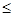 ε – нет,
ε – нет,
|x4(3)-x4(2)| = |0,336–0,308| = 0,028 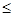 ε – нет.
ε – нет.
Выполним четвёртую итерацию.
Подставим значения, полученные в третьем приближении, в итерационные формулы и вычислим значения неизвестных при четвертом приближении.
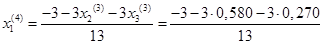 = -0,427
= -0,427
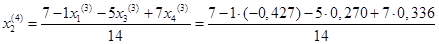 = 0,602
= 0,602
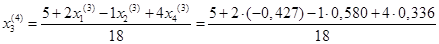 = 0,273
= 0,273
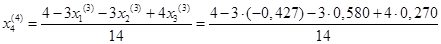 = 0,330
= 0,330
Выполним проверку полученных значений:
|x1(4)-x1(3)| = |-0,427+0,427| = 0,000 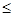 ε – да,
ε – да,
|x2(4)-x2(3)| = |0,602–0,580| = 0,022 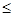 ε – нет,
ε – нет,
|x3(4)-x3(3)| = |0,273–0,270| = 0,003 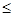 ε – нет,
ε – нет,
|x4(4)-x4(3)| = |0,330–0,336| = 0,006 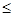 ε – нет.
ε – нет.
Выполним пятую итерацию.
Подставим значения, полученные в четвертом приближении, в итерационные формулы и вычислим значения неизвестных при пятом приближении.
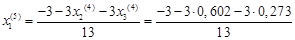 = -0,433
= -0,433
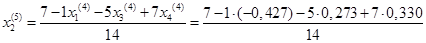 = 0,598
= 0,598
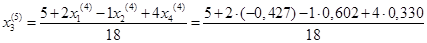 = 0,270
= 0,270
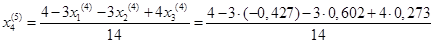 = 0,326
= 0,326
Выполним проверку полученных значений:
|x1(5)-x1(4)| = |-0,433+0,427| = 0,006  ε – нет,
ε – нет,
|x2(5)-x2(4)| = |0,598–0,602| = 0,004  ε – нет,
ε – нет,
|x3(5)-x3(4)| = |0,270–0,273| = 0,003  ε – нет,
ε – нет,
|x4(5)-x4(4)| = |0,326–0,330| = 0,004  ε – нет.
ε – нет.
Выполним шестую итерацию.
Подставим значения, полученные в пятом приближении, в итерационные формулы и вычислим значения неизвестных при шестом приближении.
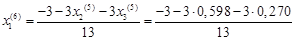 = -0,431
= -0,431
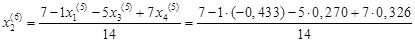 = 0,597
= 0,597
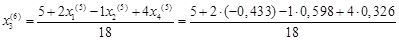 = 0,269
= 0,269
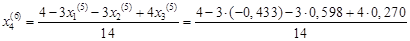 = 0,327
= 0,327
Выполним проверку полученных значений:
|x1(6)-x1(5)| = |-0,431+0,433| = 0,002  ε – нет,
ε – нет,
|x2(6)-x2(5)| = |0,597–0,598| = 0,001  ε – да,
ε – да,
|x3(6)-x3(5)| = |0,269–0,270| = 0,001  ε – да,
ε – да,
|x4(6)-x4(5)| = |0,327–0,326| = 0,001  ε – да.
ε – да.
Выполним седьмую итерацию.
Подставим значения, полученные в шестом приближении, в итерационные формулы и вычислим значения неизвестных при седьмом приближении.
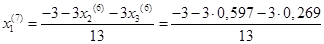 = -0,431
= -0,431
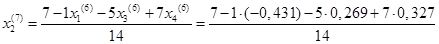 = 0,598
= 0,598
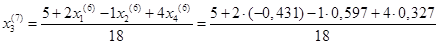 = 0,269
= 0,269
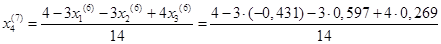 = 0,327
= 0,327
Выполним проверку полученных значений:
|x1(7)-x1(6)| = |-0,431+0,431| = 0,000  ε – да,
ε – да,
|x2(7)-x2(6)| = |0,598–0,597| = 0,001  ε – да,
ε – да,
|x3(7)-x3(6)| = |0,269–0,269| = 0,000  ε – да,
ε – да,
|x4(7)-x4(6)| = |0,327–0,327| = 0,000  ε – да.
ε – да.
Необходимая точность достигается в седьмой итерации.
Ответ: х1 = -0,431,
х2 = 0,598,
х3 = 0,269,
х4 = 0,327.
Метод Зейделя
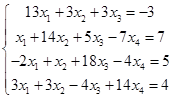
Условия сходимости было проверено выше, оно выполняется.
Точность вычисления ε  0,001.
0,001.
Примем за нулевое приближение неизвестных значений, равные нулю.
x1(0) = x2(0) = x3(0) = x4(0) = 0;
Подставим полученные значения в итерационные формулы и вычислим значения неизвестных при первом приближении.
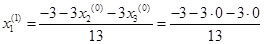 = -0,231
= -0,231
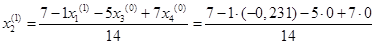 = 0,517
= 0,517
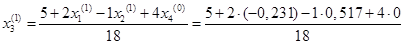 = 0,223
= 0,223
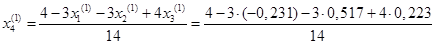 = 0,288
= 0,288
Выполним проверку полученных значений:
|x1(1)-x1(0)| = |-0,231–0| = 0,231  ε – нет
ε – нет
|x2(1)-x2(0)| = |0,517–0| = 0,517  ε – нет
ε – нет
|x3(1)-x3(0)| = |0,223–0| = 0,223  ε – нет
ε – нет
|x4(1)-x4(0)| = |0,288–0| = 0,288  ε – нет
ε – нет
Выполним вторую итерацию.
Подставим значения, полученные в первом приближении, в итерационные формулы и вычислим значения неизвестных при втором приближении.
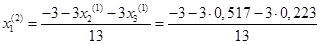 = -0,402
= -0,402
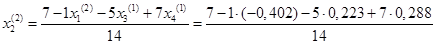 = 0,593
= 0,593
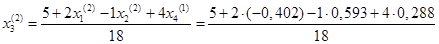 = 0,264
= 0,264
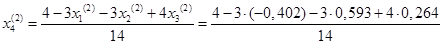 = 0,320
= 0,320
Выполним проверку полученных значений:
|x1(2)-x1(1)| = |-0,402+0,231| = 0,171  ε – нет,
ε – нет,
|x2(2)-x2(1)| = |0,593–0,517| = 0,076  ε – нет,
ε – нет,
|x3(2)-x3(1)| = |0,264–0,223| = 0,041  ε – нет,
ε – нет,
|x4(2)-x4(1)| = |0,320–0,288| = 0,032  ε – нет.
ε – нет.
Выполним третью итерацию.
Подставим значения, полученные во втором приближении, в итерационные формулы и вычислим значения неизвестных при третьем приближении.
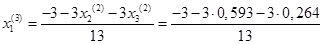 = -0,429
= -0,429
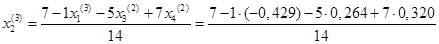 = 0,596
= 0,596
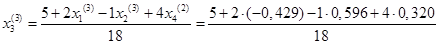 = 0,268
= 0,268
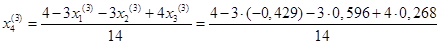 = 0,326
= 0,326
Выполним проверку полученных значений:
|x1(3)-x1(2)| = |-0,429+0,402| = 0,027  ε – нет,
ε – нет,
|x2(3)-x2(2)| = |0,596–0,593| = 0,003  ε – нет,
ε – нет,
|x3(3)-x3(2)| = |0,268–0,264| = 0,004  ε – нет,
ε – нет,
|x4(3)-x4(2)| = |0,326–0,320| = 0,006  ε – нет.
ε – нет.
Выполним четвёртую итерацию.
Подставим значения, полученные в третьем приближении, в итерационные формулы и вычислим значения неизвестных при четвёртом приближении.
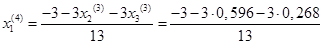 = -0,430
= -0,430
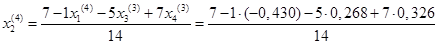 = 0,598
= 0,598
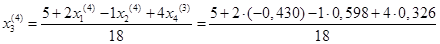 = 0,269
= 0,269
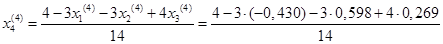 = 0,327
= 0,327
Выполним проверку полученных значений:
|x1(4)-x1(3)| = |-0,430+0,429| = 0,01  ε – да,
ε – да,
|x2(4)-x2(3)| = |0,598–0,596| = 0,002  ε – нет,
ε – нет,
|x3(4)-x3(3)| = |0,269–0,268| = 0,001  ε – да,
ε – да,
|x4(4)-x4(3)| = |0,327–0,326| = 0,001  ε – да.
ε – да.
Выполним пятую итерацию.
Подставим значения, полученные в четвёртом приближении, в итерационные формулы и вычислим значения неизвестных при пятом приближении.
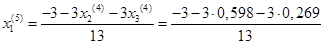 = -0,431
= -0,431
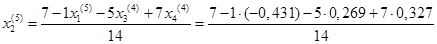 = 0,598
= 0,598
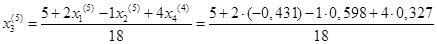 = 0,269
= 0,269
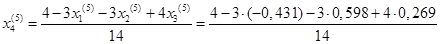 = 0,327
= 0,327
Выполним проверку полученных значений:
|x1(5)-x1(4)| = |-0,431+0,430| = 0,001  ε – да,
ε – да,
|x2(5)-x2(4)| = |0,598–0,598| = 0,000  ε – да,
ε – да,
|x3(5)-x3(4)| = |0,269–0,269| = 0,000  ε – да,
ε – да,
|x4(5)-x4(4)| = |0,327–0,327| = 0,000  ε – да.
ε – да.
Необходимая точность достигается в пятой итерации.
Ответ: х1 = -0,431,
х2 = 0,598,
х3 = 0,269,
х4 = 0,327.
|
из
5.00
|
Обсуждение в статье: Метод простой итерации |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

