 |
Главная |
Метод разделения переменных. Уравнение свободных колебаний струны
|
из
5.00
|
Метод разделения переменных или метод Фурье, является одним из наиболее распространенных методов решения уравнений с частными производными. Изложение этого метода мы проведем для задачи о колебаниях струны, закрепленной на концах. Итак, будем искать решение уравнения

удовлетворяющее однородным граничным условиям
 (9)
(9)
и начальным условиям
 (10)
(10)
Уравнение (1) линейно и однородно, поэтому сумма частных решений также является решением этого уравнения. Имея достаточно большое число частных решений, можно попытаться при помощи суммирования их с некоторыми коэффициентами найти искомое решение.
Поставим основную вспомогательную задачу: найти решение уравнения
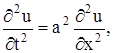
не равное тождественно нулю, удовлетворяющее однородным граничным условиям
 (11)
(11)
и представимое в виде произведения
 (12)
(12)
где X (x) – функция только переменного x, T (t) – функция только переменного t.
Подставляя предполагаемую форму решения (12) в уравнение (1), получим:

или, после деления на XT,
 (13)
(13)
Чтобы функция (12) была решением уравнения (1), равенство (13) должно удовлетворяться тождественно, т. е. 0 ‹ х ‹  , t › 0. Правая часть равенства (13) является функцией только переменного t, а левая – только х. Фиксируя, например, некоторое значение х и меняя t (или наоборот), получим, что правая и левая части равенства (13) при изменении своих аргументов сохраняют постоянное значение
, t › 0. Правая часть равенства (13) является функцией только переменного t, а левая – только х. Фиксируя, например, некоторое значение х и меняя t (или наоборот), получим, что правая и левая части равенства (13) при изменении своих аргументов сохраняют постоянное значение
 (14)
(14)
где  – постоянная, которую для удобства последующих выкладок берем со знаком минус, ничего не предполагая при этом о ее знаке.
– постоянная, которую для удобства последующих выкладок берем со знаком минус, ничего не предполагая при этом о ее знаке.
Из соотношения (14) получаем обыкновенные дифференциальные уравнения для определения функций X (x) и T (t)
 (15)
(15)
 (16)
(16)
Граничные условия (11) дают:
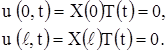
Отсюда следует, что функция X (x) должна удовлетворять дополнительным условиям:
X(0) = X(  ) = 0, (17)
) = 0, (17)
Так как иначе мы имели бы

в то время как задача состоит в нахождении нетривиального решения. Для функции T (t) в основной вспомогательной задаче никаких дополнительных условий нет.
Таким образом, в связи с нахождением функции X (x) мы приходим к простейшей задаче о собственных значениях: найти те значения параметра  , при которых существуют нетривиальные решения задачи:
, при которых существуют нетривиальные решения задачи:
 (18)
(18)
а также найти эти решения. Такие значения параметра  называются собственными значениями, а соответствующие им нетривиальные решения – собственными функциями задачи (18). Сформулированную таким образом задачу часто называют задачей Штурма – Лиувилля.
называются собственными значениями, а соответствующие им нетривиальные решения – собственными функциями задачи (18). Сформулированную таким образом задачу часто называют задачей Штурма – Лиувилля.
Рассмотрим отдельно случаи, когда параметр  отрицателен, равен нулю или положителен.
отрицателен, равен нулю или положителен.
1. При  ‹ 0 задача не имеет нетривиальных решений. Действительно, общее решение уравнения (15) имеет вид
‹ 0 задача не имеет нетривиальных решений. Действительно, общее решение уравнения (15) имеет вид
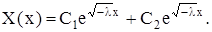
Граничные условия дают:
Х (0) = С1 + С2 = 0;


т. е.

Но в рассматриваемом случае  – действительно и положительно, так что
– действительно и положительно, так что  . Поэтому
. Поэтому
С1 =0, С2 = 0
и, следовательно,
Х (х)  0.
0.
2. При  = 0 также не существует нетривиальных решений. Действительно, в этом случае общее решение уравнения (15) имеет вид
= 0 также не существует нетривиальных решений. Действительно, в этом случае общее решение уравнения (15) имеет вид
Х (х) = С1х + С2.
Граничные условия дают:

т. е. С1 = 0 и С2 = 0 и, следовательно,
Х (х)  0.
0.
3. При  › 0 общее решение уравнения может быть записано в виде
› 0 общее решение уравнения может быть записано в виде

Граничные условия дают:

Если Х(х) не равно тождественно нулю, то D2  0, поэтому
0, поэтому
 (19)
(19)
Или

где n- любое целое число. Следовательно, нетривиальные решения задачи (18) возможны лишь при значениях

Этим собственным значениям соответствуют собственные функции

где Dn – произвольная постоянная.
Итак, только при значениях  , равных
, равных
 (20)
(20)
существуют нетривиальные решения задачи (11)
 (21)
(21)
определяемые с точностью до произвольного множителя, который мы положили равным единице. Этим же значениям  n соответствуют решения уравнения (9)
n соответствуют решения уравнения (9)
 (22)
(22)
где An и Bn – произвольные постоянные.
Возвращаясь к задаче (1), (9), (10), заключаем, что функции
 (23)
(23)
являются частными решениями уравнения (1), удовлетворяющими граничным условиям (11) и представимыми в виде произведения (12) двух функций, одна из которых зависит только от х, другая – от t. Эти решения могут удовлетворить начальным условиям (10) нашей исходной задачи только для частных случаев начальных функций j(x) и y(x).
Обратимся к решению задачи (1), (9), (10) в общем случае. В силу линейности и однородности уравнения (1) сумма частных решений
 (24)
(24)
также удовлетворяет этому уравнению и граничным условиям (9). Начальные условия позволяют определить An и Bn. Потребуем, чтобы функция (24) удовлетворяла условиям (10)
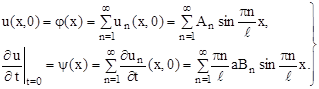 (25)
(25)
Из теории рядов Фурье известно, что произвольная кусочно-непрерывная и кусочно-дифференцируемая функция f(x), заданная в промежутке  , разлагается в ряд Фурье
, разлагается в ряд Фурье
 (26)
(26)
где
 (27)
(27)
Если функции j(x) и y(x) удовлетворяют условиям разложения в ряд Фурье, то
 (28)
(28)
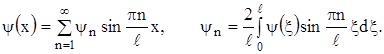 (29)
(29)
Сравнение этих рядов с формулами (25) показывает, что для выполнения начальных условий надо положить
 (30)
(30)
чем полностью определяется функция (24), дающая решение исследуемой задачи.
Итак, мы доказали, что ряд (24), где коэффициенты An и Bn определены по формуле (30), если он допускает двукратное почленное дифференцирование, представляет функцию u (x, t), которая является решением уравнения (1) и удовлетворяет граничным и начальным условиям (9) и (10).
Замечание. Решая рассмотренную задачу для волнового уравнения другим методом, можно доказать, что ряд (24) представляет решение и в том случае, когда он не допускает почленного дифференцирования. При этом функция  должна быть дважды дифференцируемой, а
должна быть дважды дифференцируемой, а  - один раз дифференцируемой.
- один раз дифференцируемой.
Решение уравнений
1. Найти решение уравнения:
 , если
, если  ,
, 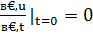 .
.
Решение:
Так как  , а
, а  , то
, то
 ,
,
где  . Таким образом,
. Таким образом,  , или
, или 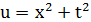 .
.
2. Найти форму струны, определяемой уравнением  в момент
в момент  , если
, если
3.  ,
,  .
.
Решение:
Имеем
 ,
,
т.е.
 , или
, или  .
.
Если  , то
, то  , т.е. струна параллельна оси абсцисс.
, т.е. струна параллельна оси абсцисс.
4. Струна, закрепленная на концах  и
и  , имеет в начальный момент форму параболы
, имеет в начальный момент форму параболы  .
.

5. Определить смещение точек струны от оси абсцисс, если начальные скорости отсутствуют.
Решение:
Здесь  ,
,  . Находим коэффициенты ряда, определяющего решение уравнения колебания струны:
. Находим коэффициенты ряда, определяющего решение уравнения колебания струны:
 ;
;  .
.
Для нахождения коэффициента  дважды интегрируем по частям:
дважды интегрируем по частям:
 ,
,  ,
,  ,
,  ;
;
 ,
,
т.е.

 ,
, 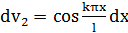 ,
,  ,
,  ;
;
 =
=
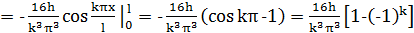 .
.
Подставляя выражения для  и
и 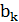 получим:
получим:
 .
.
Если  , то
, то  , а если
, а если  , то
, то 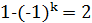 ; поэтому окончательно имеем
; поэтому окончательно имеем

Пусть начальные отклонения струны, закрепленной в точках  и
и  , равны нулю, а начальная скорость выражается формулой
, равны нулю, а начальная скорость выражается формулой

Определить форму струны для любого момента времени t.
Решение:
Здесь  , а
, а  в интервале
в интервале  ,
,  и
и  вне этого интервала.
вне этого интервала.
Следовательно,  ;
;


Отсюда

Или


|
из
5.00
|
Обсуждение в статье: Метод разделения переменных. Уравнение свободных колебаний струны |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

