 |
Главная |
Глава 2. Уравнения параболического типа
|
из
5.00
|
2.1 Уравнение распространения тепла в стержне
Рассмотрим однородный стержень длины  . Будем предполагать, что боковая поверхность стержня теплонепроницаема и что во всех точках поперечного сечения стержня температура одинакова. Изучим процесс распространения тепла в стержне.
. Будем предполагать, что боковая поверхность стержня теплонепроницаема и что во всех точках поперечного сечения стержня температура одинакова. Изучим процесс распространения тепла в стержне.
Расположим ось Ох так, что один конец стержня будет совпадать с точкой х = 0, а другой – с точкой х =  .
.

Рис. 2.1.
Пусть u (x, t) – температура в сечении стержня с абсциссой х в момент t. Опытным путем установлено, что скорость распространения тепла, т. е. количество тепла, протекающего через сечение с абсциссой х за единицу времени, определяется формулой
 (1)
(1)
где S – площадь сечения рассматриваемого стержня, k – коэффициент теплопроводности.
Рассмотрим элемент стержня, заключенный между сечениями с абсциссами х1 и х2 (х2 – х1 =  х). Количество тепла, прошедшего через сечение с абсциссой х1 за время
х). Количество тепла, прошедшего через сечение с абсциссой х1 за время  t, будет равно
t, будет равно
 (2)
(2)
то же самое с абсциссой х2:
 (3)
(3)
Приток  Q1 -
Q1 -  Q2 в элемент стержня за время
Q2 в элемент стержня за время  t будет равняться:
t будет равняться:
 (4)
(4)
Этот приток тепла за время  t затратился на повышение температуры элемента стержня на величину
t затратился на повышение температуры элемента стержня на величину  u:
u:

Или
 (5)
(5)
где с – теплоемкость вещества стержня,  – плотность вещества стержня (
– плотность вещества стержня ( 
 xS – масса элемента стержня).
xS – масса элемента стержня).
Приравнивая выражения (4) и (5) одного и того же количества тепла  , получим:
, получим:
|

Это и есть уравнение распространения тепла (уравнение теплопроводности) в однородном стержне.
Чтобы решение уравнения (6) было вполне определено, функция u (x, t) должна удовлетворять краевым условиям, соответствующим физическим условиям задачи. Краевые условия для решения уравнения (6) могут быть различные. Условия, которые соответствуют так называемой первой краевой задаче для  , следующие:
, следующие:
u (x, 0) = φ(x), (7)
u (0, t) = ψ1(t), (8)
u (  , t) = ψ2(t). (9)
, t) = ψ2(t). (9)
Физическое условие (7) (начальное условие) соответствует тому, что при  в разных сечениях стержня задана температура, равная φ(x). Условия (8) и (9) (граничные условия) соответствуют тому, что на концах стержня при х = 0 и при х =
в разных сечениях стержня задана температура, равная φ(x). Условия (8) и (9) (граничные условия) соответствуют тому, что на концах стержня при х = 0 и при х =  поддерживается температура, равная ψ1(t) и ψ2(t) соответственно.
поддерживается температура, равная ψ1(t) и ψ2(t) соответственно.
Доказывается, что уравнение (6) имеет единственное решение в области  , удовлетворяющее условиям (7) – (9).
, удовлетворяющее условиям (7) – (9).
Решение задач
1. Задача:
Решить уравнение
 .
.
Решение. Составим и решим систему уравнений характеристик

Уравнение  даёт первый интеграл
даёт первый интеграл  . Преобразуем три дроби
. Преобразуем три дроби  , используя правило работы с равными дробями:
, используя правило работы с равными дробями:
 .
.
Отсюда получим второй первый интеграл
 .
.
Возьмём следующее уравнение  , подставим
, подставим  и
и  в это уравнение, получим
в это уравнение, получим
 .
.
Решим полученное линейное уравнение:
 .
.
Получим третий первый интеграл
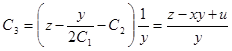 .
.
2. Задача
Найти общее решение уравнения
 .
.
Решение: Составим и решим систему уравнений характеристик

Первый интеграл равен  . Функция
. Функция  вида
вида  , где
, где  - произвольная дифференцируемая функция, является общим решением уравнения.
- произвольная дифференцируемая функция, является общим решением уравнения.
3. Задача
Решить уравнение
 .
.
Решение. Составим систему уравнений характеристик
 .
.
Первая пара дробей даёт первый интеграл

Подставим  во вторую пару дробей, получим
во вторую пару дробей, получим
 .
.
Интегрируя последнее уравнение, получим второй первый интеграл
 .
.
Общее решение имеет вид
 .
.
4. Задача
Решение задачу Коши
 .
.
Решение. Найдем два первых интеграла. Составим систему
 гиперболический колебание дифференциальный теплопроводность интеграл
гиперболический колебание дифференциальный теплопроводность интеграл
Отсюда получим первый интеграл  .
.
Решая уравнение  при условии, что
при условии, что  , получим второй первый интеграл
, получим второй первый интеграл

Подставим  в два первых интеграла:
в два первых интеграла:

Исключая  из этой пары равенств, получим связь между первыми интегралами
из этой пары равенств, получим связь между первыми интегралами  . Подставляя вместо
. Подставляя вместо  и
и  первые интегралы, получим решение задачи Коши:
первые интегралы, получим решение задачи Коши: 
5. Задача
Решить задачу Коши  ,
,  .
.
Решение. Найдем первые интегралы системы уравнений характеристики  ; они равны
; они равны
 ,
,  .
.
Найдём, используя начальные данные, связь между первыми интегралами:


 .
.
Подставим первые интегралы  и
и  , получим решение:
, получим решение:
 .
.
6. Решить уравнение  для следующего начального распределения температуры стержня:
для следующего начального распределения температуры стержня:
 .
.
Решение: Стержень является бесконечным, поэтому решение запишется в виде интеграла Пуассона:

Так как  в интервале
в интервале  равна постоянной температуре
равна постоянной температуре  , а вне интервала температура равна нулю, то решение примет вид
, а вне интервала температура равна нулю, то решение примет вид

Полученный результат можно преобразовать к интегралу вероятностей:
 .
.
Действительно полагая  ,
,  , получим
, получим


Таким образом, решение выразится формулой

Графиком функции  является кривая:
является кривая:

Найти решение уравнения  , удовлетворяющее начальному условию
, удовлетворяющее начальному условию  и краевому условию
и краевому условию  .
.
Решение: Здесь мы имеем дифференциальное уравнение теплопроводности для полубесконечного стержня. Решение, удовлетворяющее указанным условиям, имеет вид
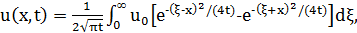
Или

Полагая  ,
,  , преобразуем первый интеграл, пользуясь интегралом вероятностей, т.е.
, преобразуем первый интеграл, пользуясь интегралом вероятностей, т.е.

Полагая  ,
,  , получим
, получим

Таким образом, решение принимает вид

Заключение
В курсовой работе приведены некоторые примеры применения дифференциальных уравнений для моделирования таких реальных процессов, как колебания струны, распространение тепла в стержне.
Работа начинается с рассмотрения простейших задач, приводящих к дифференциальным уравнениям гиперболического типа (колебания струны, электрические колебания в проводах). Затем рассматривается один из методов решения уравнений данного типа. Во второй главе рассматриваются дифференциальные уравнения параболического типа (распространение тепловых волн) и одно из приложений к данной сфере – температурные волны.
Вследствие большого объема теории по применению дифференциальных уравнений для моделирования реальных процессов в данной курсовой работе не мог быть рассмотрен весь материал.
В заключение хотелось бы отметить особую роль дифференциальных уравнений при решении многих задач математики, физики и техники, так как часто не всегда удается установить функциональную зависимость между искомыми и данными переменными величинами, но зато удается вывести дифференциальное уравнение, позволяющее точно предсказать протекание определенного процесса при определенных условиях.
Литература
1. Н. С. Пискунов "Дифференциальное и интегральное исчисления", М., "Наука", 1972, том. 2.
2. И. М. Уваренков, М. З. Маллер "Курс математического анализа", М., "Просвещение", 1976.
3. А. Н. Тихонов, А. А. Самарский "Уравнения математической физики", М., "Наука", 1972.
4. Владимиров В. С. "Уравнения математической физики", М., "Наука", 1988.
|
из
5.00
|
Обсуждение в статье: Глава 2. Уравнения параболического типа |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

